Математика/1.Дифференциальные и интегральные уравнения

к.ф.-м.н. Сарсекеева А.С.

Казахский национальный университет имени аль-Фараби, Казахстан

Разрешимость модельной задачи

в пространстве Соболева

Пусть

Требуется найти функции , и по условиям

в (1)

в (2)

(3)

(4)

где b, c, κ, d_m – постоянные коэффициенты,

Задача (1) - (4) исследована в пространстве Соболева. Дадим определение пространств [1].

, , - банахово пространство функций , имеющих норму

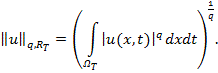
, l- целое, - банахово пространство функций, имеющих норму

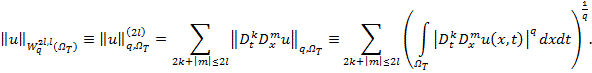
, , l- нецелое, - банахово пространство функций , имеющих норму

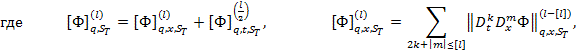
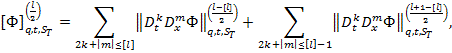
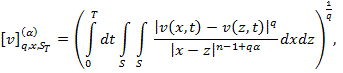
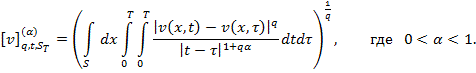
Теорема. Для любой функции , задача (1) - (4) имеет единственное решение , , , для которого справедлива оценка

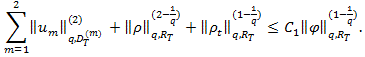(5)

Доказательство. Применяя преобразования Фурье по и Лапласа по , найдем решение задачи (1) - (4) с производной по времени в граничном условии в виде

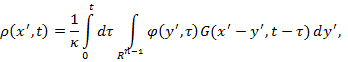
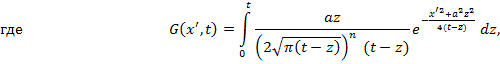
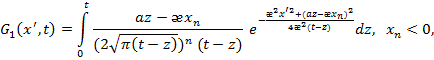
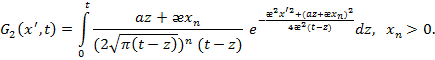
Покажем, что функции и удовлетворяют оценке

(6)

Для этого используем определение нормы функции :

Выражая функцию через из уравнений и условий задачи (1) - (4), получим задачу для функций рассмотренную в [2]. Аналогично тому, как это сделано в работе [1], можем доказать, что функции и выполняется оценка

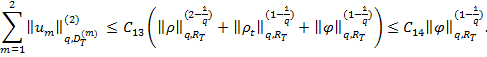(7)

Из оценок (6) и (7) следует справедливость оценки (5). Тем самым теорема доказана.

Литература:

1. Ладыженская О.А., Солонников В.А., Уральцева Н.Н. Линейные и квазилинейные уравнения параболического типа. М. :Наука, 1967. 736с.

2. Бижанова Г.И. Оценки решения n-мерной задачи сопряжения для уравнения теплопроводности в весовых гельдеровских нормах I,II //Изв. АН РК, серия физ.-мат., 1992. №5. С.7-13; Изв. АН РК, серия физ.-мат., 1993. №1. С.11-17 с.