Сатыбалдиев О.С. д.п.н., профессор,

Абдукулова Т.А., Сержан Г. – магистранты

Қ.И.Сәтбаев атындағы Қазақ ұлттық техникалық университеті

Тікбұрышты формадағы облыстың контурында берілген бастапқы шарттары бойынша мұнай қатпарының қысымын табу

Мұнай қабаттары өте жоғары қысымдағы мұнаймен қорланған кеуек орта болып табылады. Қабаттың кезкелген нүктесінде қысымының таралуы

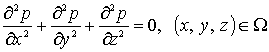(1)

түріндегі Лаплас теңдеуін қанағаттандырады.

Қабаттың қуаты өте аз болған жағдайда вертикаль өсіндегі қысымның өзгеруін елемеуге болады. Бұл жағдайда кеңістікте қаралған есептер жазықтықта қарастырылатын есептерге келтіріледі яғни (1) теңдеу

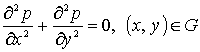. (2)

түрінде қарастырылады.

Скважинаның дебиттерін анықтау, скважинаның үйлесімді орналасу жүйесін таңдау, мұнайлы контурлардың орналасуы және т.б. секілді жерасты гидравликасының техникалық есептері (1) және (2) дифференциалдық теңдеулердің шешімін табу мәселелеріне алып келеді.

Кезкелген кесінді мұнай контуры үшін және скважинаның кезкелген орналасуы жағдайында бұл айтылған мәселелердің дәл шешімі жоқ. Алайда (1) немесе (2) теңдеулерге сәйкес жоғарыда қарастырылған есептерді дұрыс геометриялық формадағы облыстарда қарастыруға болады.

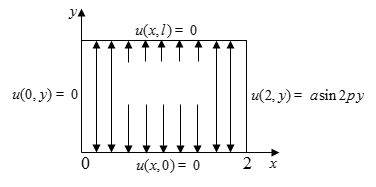
Мынандай есепті қарастыралық. Тіктөртбұрышты формадағы обылысы берілсін. Осы облыстың контурындағы қысымы

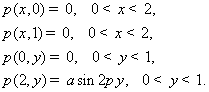
шарттарын қанағаттандырсын. облысындағы мұнай қабатының қысымын табалық.

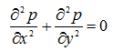
Біз жоғарыда мұнай қабатының кезкелген нүктесіндегі қысым , Лаплас теңдеуін қанағаттандыратындығы туралы айтқанбыз. Олай болса бұл есепті төмендегідей тұжырымдауға болады:

шекаралық шарттарды қанағаттандыратын

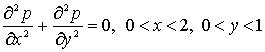
Лаплас теңдеуінің облысындағы шешімін табу керек.

Есептің шешімін іздеу үшін айнымалыларды болу әдісін пайдаланамыз, Лаплас теңдеуінің шешімін

.

Осы -ның мәнін (2) теңдеуге қойып `

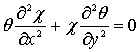
немесе

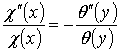
теңдеуін аламыз. Соңғы теңдеудің сол жағы тек қана -ке, ал оң жағы тек қана -ке тәуелді және олар кезкелген пен үшін өзара тең. Бұл жағдай

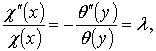
болғанда ғана орындалады (мұндағы ). Осы теңдеуден және функцияларына қарағанда

(3)

(4)

қарапайым дифференциалдық теңдеулерін аламыз. (3) пен (4) теңдеулердің шешімі -ның таңбасына тәуелді. -ға байланысты бұл теңдеулердің келесі шешімдерін аламыз:

(5)

(6)

(7)

мұндағы А, В, С, Д кезкелген тұрақты сандар. Кей уақытта (5) мен (6) теңдеулердің орнына

(8)

(9)

теңдеулерін пайдаланған тиімді.

Енді жоғарыдағы есепке оралайық. шекаралық шартындағы алғашқы екі шарт функциясының -ке қарағанда тақ екендігін көрсетеді. Сондықтан бұл шекаралық шарттарды қанағаттандыратын құрамында бар шешімді таңдаймыз, яғни (7) теңдікпен анықталған

теңдігін аламыз. Осыдан . Олай болса

Мұндағы -ның екінші шартынан теңдігін аламыз. Осыдан және демек, – ның үшінші шартынан

теңдігін аламыз. Соңғы теңдік кезкелген үшін орындалады, сондықтан немесе . Сонымен

– ның соңғы шартынан

, .

теңдігін аламыз. Біз және деп таңдауға тиіспіз, яғни немесе .

Сонымен қарастырылып отырған есебіміздің шешімі

(10)

болады.

Әдебиет

1. Яглом И.М. Математические структуры и математическое моделирование. – М., Наука, 2007.

2. Гусейнзаде М.А. и др. Применение обобщенных функций в задачах трубопроводного транспорта нефти и газа. – М.:РГУ нефти и газа им. И.М. Губкина, 2011.

3. Маскет М. Физические основы технологии добычи нефти. – М.: Институт компьютерных исследований, 2010.