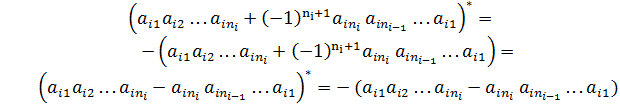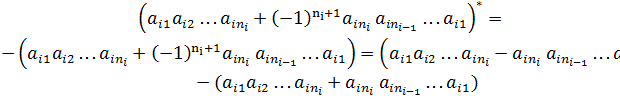Mathematics / 1.Differential and integral equations
Arzikulov F., Mamatohunova Y.
Andijan state university, Uzbekistan
On purely real lie algebras of
skew-adjoint operators
ABSTRACT. In
the given paper we investigate a real von Neumann algebra  on
a Hilbert space such that
on
a Hilbert space such that  and a real Lie algebra
and a real Lie algebra  of
skew-adjoint operators on a Hilbert space H such that
of
skew-adjoint operators on a Hilbert space H such that  for the real *-algebra
for the real *-algebra  , generated by
, generated by  in
in
 . These algebras are called a purely real
von Neumann algebra and a purely real Lie algebra respectively.
. These algebras are called a purely real
von Neumann algebra and a purely real Lie algebra respectively.
An analog of Gelfand-Naumark theorem for ultraweakly
closed purely real Lie algebras of skew-adjoint operators on a Hilbert space is
proved. Also, it is proved that the enveloping C* -algebra of such
Lie algebra is a von Neumann algebra if this Lie algebra is reversible and it
is given a condition in which a purely real Lie algebra of skew-adjoint
operators is reversible.
Introduction
A weakly closed real *-subalgebra  in B(H) is called a purely real von Neumann algebra if
in B(H) is called a purely real von Neumann algebra if  , where
, where  . Let
. Let  be
the center of
be
the center of  . If
. If  consists of real multiples of 1, i.e.
consists of real multiples of 1, i.e.  , then R is said to be a purely real
factor. Given a purely real von Neumann algebra
, then R is said to be a purely real
factor. Given a purely real von Neumann algebra  it
is easy to see that the set
it
is easy to see that the set  forms a Lie algebra with the multiplication
forms a Lie algebra with the multiplication  . Such Lie algebras and purely real von
Neumann algebras were investigated, in particular, in papers
. Such Lie algebras and purely real von
Neumann algebras were investigated, in particular, in papers  by
Sh.Ayupov. In these papers it was considered a spacial case of a more general
algebraic problem: letting
by
Sh.Ayupov. In these papers it was considered a spacial case of a more general
algebraic problem: letting  and
and  be
simple or prime rings with involutions, can every (Lie) isomorphism of
be
simple or prime rings with involutions, can every (Lie) isomorphism of  onto
onto  be
lifted to an (associative) isomorphism of
be
lifted to an (associative) isomorphism of  onto
onto  ? Here the derived Lie ring
? Here the derived Lie ring  is
the additive span of all commutators
is
the additive span of all commutators  ,where
,where  ; it is a Lie ideal in Lie ring
; it is a Lie ideal in Lie ring  .
.
The above problem was solved for simple rings with involution of the
first kind were obtained by Martindale  and for arbitrary kind by Rosen
and for arbitrary kind by Rosen  . But in the case of prime rings it is not
possible in general to extend a Lie isomorphism between
. But in the case of prime rings it is not
possible in general to extend a Lie isomorphism between  and
and  to a *-isomorphism between whole
to a *-isomorphism between whole  and
and  . Moreover, there are examples of prime
rings with involution such that
. Moreover, there are examples of prime
rings with involution such that  and
and  are Lie isomorphic but
are Lie isomorphic but  and
and  are not *-isomorphic. Concerning purely real von Neumann algebras
one can see that every purely real von Neumann algebra is semiprime: it is
prime if (but not only if) it is a purely real factor. Examples of simple
purely real factors are given by factors of type
are not *-isomorphic. Concerning purely real von Neumann algebras
one can see that every purely real von Neumann algebra is semiprime: it is
prime if (but not only if) it is a purely real factor. Examples of simple
purely real factors are given by factors of type  (n <
(n <  ),
),  , and à-finite type III [4].
, and à-finite type III [4].
In  it
was proved that if
it
was proved that if  and
and  are real factors not of types
are real factors not of types  and
and  then derived Lie algebras
then derived Lie algebras
 and
and  are isomorphic if and only if
are isomorphic if and only if  and
and  are *-isomorphic.
are *-isomorphic.
Also in the paper  there were proved the following statements: let
there were proved the following statements: let  be
a purely real factor except types
be
a purely real factor except types  and
and  . Then
. Then
1. 
2.  , where Rk is the associative
subalgebra generated by
, where Rk is the associative
subalgebra generated by  .
.
In the given paper analogues of these statements are proved for real von
Neumann algebras  ,
,  , satisfying the conditions
, satisfying the conditions  ,
,  , where
, where  ,
,  are the real von Neumann subalgebras generated by
are the real von Neumann subalgebras generated by  ,
,  respectively.
respectively.
In the given paper it is introduced weakly closed purely real Lie
algebras on a complex Hilbert space. These Lie algebras are Banach Lie algebras
over the field of real numbers. Banach Lie algebras are investigated in  ,
,  . In this paper we give a representation
of all maximal purely real Lie algebras of skew-adjoint elements in the algebra
. In this paper we give a representation
of all maximal purely real Lie algebras of skew-adjoint elements in the algebra
 for a complex Hilbert space
for a complex Hilbert space  .
.
Also, it is proved that the enveloping C*-algebra of such Lie algebra is
a von Neumann algebra if this Lie algebra is reversible. Also, it is found a
condition in which case a purely real Lie algebra of skew-adjoint operators is
reversible.
1.
Maximal purely real Lie algebras of
skew-adjoint operators
In  it
was proved the following theorem.
it
was proved the following theorem.
Theorem 1.1. Let H be a Hilbert space. Then any maximal
purely real *-algebra on
 is
isomorphic to the algebra
is
isomorphic to the algebra 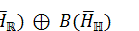 , where
, where  and
and  are Hilbert subspaces of
are Hilbert subspaces of  such that
such that 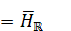
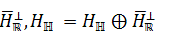 , the identity elements of the algebras
, the identity elements of the algebras 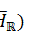 and
and 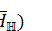 are mutually orthogonal and their sum is equal to the
identity element of
are mutually orthogonal and their sum is equal to the
identity element of  , and
, and  and
and  are Hilbert spaces on
are Hilbert spaces on  and
and  respectively such that
respectively such that 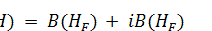 , where
, where 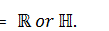
Definition 1.2. Let  be
an Lie algebra of skew-adjoint operators on a Hilbert space
be
an Lie algebra of skew-adjoint operators on a Hilbert space  . The Lie algebra L is called a purely real Lie algebra, if the real *-algebra
. The Lie algebra L is called a purely real Lie algebra, if the real *-algebra  , generated by
, generated by  in
in
 satisfies to the condition
satisfies to the condition  (L) ∩ iR(L) = {0
(L) ∩ iR(L) = {0 .
.
By Zorn’s lemma for any purely real Lie algebra of skew-adjoint operators
on a Hilbert space there exists a maximal purely real Lie algebra of
skew-adjoint operators containing the given Lie algebra. Therefore the
following theorem takes place.
Theorem 1.3. Let H be a Hilbert space. Then any maximal
purely real Lie algebra of skew-adjoint operators on H is isomorphic to the Lie
algebra 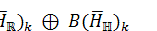 , where
, where  and
and  are Hilbert subspaces of
are Hilbert subspaces of  such that
such that 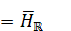
 , the identity elements of
, the identity elements of 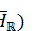 and
and  are mutually orthogonal and their sum is equal to the
identity element of
are mutually orthogonal and their sum is equal to the
identity element of 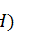 , and
, and  ,
,  are Hilbert spaces on
are Hilbert spaces on  and
and  respectively such that
respectively such that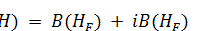 , where
, where 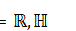 .
.
Proof. Let
 be
a maximal purely real Lie algebra of skew-adjoint operators on a Hilbert space
be
a maximal purely real Lie algebra of skew-adjoint operators on a Hilbert space  and
and  be
the real *-algebra, generated by
be
the real *-algebra, generated by  . By the definition
. By the definition  . Then there exists a maximal purely real
algebra
. Then there exists a maximal purely real
algebra  on
on
 containing the real algebra
containing the real algebra  . Since
. Since  is
maximal we have
is
maximal we have  .
.
By theorem 1.1  , where
, where  and HH are Hilbert subspaces of
and HH are Hilbert subspaces of  such that
such that 
 , the identity elements of
, the identity elements of  and
and  are mutually orthogonal and their sum is equal to the identity
element of
are mutually orthogonal and their sum is equal to the identity
element of  , and
, and  and
and  are Hilbert spaces on
are Hilbert spaces on  and
and  respectively such that
respectively such that  , where
, where  Hence
Hence  . □
. □
Definition
1.4. Let  be
an Lie algebra of skew-adjoint operators on a Hilbert space
be
an Lie algebra of skew-adjoint operators on a Hilbert space  . The Lie algebra
. The Lie algebra  is
called reversible, if for any elements
is
called reversible, if for any elements  the following conditions hold
the following conditions hold
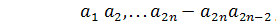 ,
,
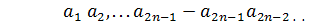 .
.
Theorem 1.5. Let  be an ultraweakly closed purely real reversible Lie
algebra of skew-adjoint operators on a Hilbert space
be an ultraweakly closed purely real reversible Lie
algebra of skew-adjoint operators on a Hilbert space  ,
, 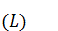 be a real von Neumann algebra, generated
by
be a real von Neumann algebra, generated
by  in
in 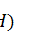 . Then
. Then 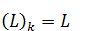 . Proof. It is evident that
. Proof. It is evident that 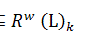 .
.
Let a  . Then a* = —a and there exists a sequence
. Then a* = —a and there exists a sequence
 such
such
that  weakly converges to a and
weakly converges to a and  where
where ,
,
 for all
for all  . Since
. Since  we
have that
we
have that  and
and
 . Then
. Then
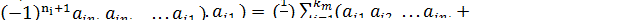 .
.
Note that in the last sum
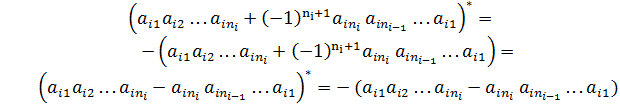
if is an even natural number for any index
is an even natural number for any index  , and
, and
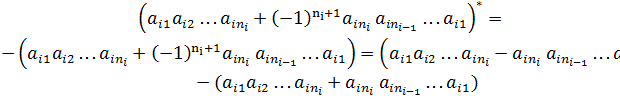
if f is an add natural number. Hence, for any
index
is an add natural number. Hence, for any
index 

by reversibility of the Lie algebra  . Therefore
. Therefore  . Since
. Since  is
ultraweakly closed in
is
ultraweakly closed in  we
have
we
have  .□
.□
Theorem 1.6. Let  be
an ultraweakly closed reversible Lie algebra of skew- adjoint operators on a
Hilbert space
be
an ultraweakly closed reversible Lie algebra of skew- adjoint operators on a
Hilbert space  ,
, 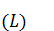 be a real von Neumann algebra, generated by
be a real von Neumann algebra, generated by  in
in  . Then the following conditions are
equivalen (1)
. Then the following conditions are
equivalen (1)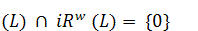 ,
,
(2)there exist Lie subalgebras 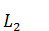 in
in
 such that
such that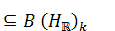 ,
, 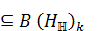 , and
, and 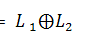 for some Hilbert spaces
for some Hilbert spaces 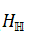 on
on  and
and  , respectively, such that
, respectively, such that 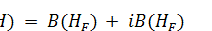 , where
, where 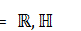 .
.
Proof.  : By theorem 1.3
: By theorem 1.3  and by theorem 4 in
and by theorem 4 in  there exist central projections
there exist central projections  and
and  in
in
 such that
such that 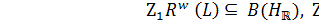 and
and  . At the same time
. At the same time  . Hence
. Hence  and
and  , where
, where 
 : The converse statement of the theorem is
obvious. □
: The converse statement of the theorem is
obvious. □
2.
Reversibility of purely real Lie algebras of
skew-adjoint
operators
Theorem 2.1. Let  be a purely real Lie algebra of skew-adjoint operators
on a Hilbert space
be a purely real Lie algebra of skew-adjoint operators
on a Hilbert space 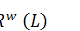 be a real von Neumann algebra, generated
by
be a real von Neumann algebra, generated
by  in
in 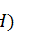 . Suppose that
. Suppose that 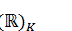 can be embedded in
can be embedded in  and in this embedding
and in this embedding 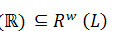 and the unit of
and the unit of 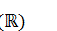 coincides with the unit of
coincides with the unit of  . Then
. Then  is reversible.
is reversible.
Proof. By
the conditions of the theorem there exists a complete system  of matrix units in
of matrix units in 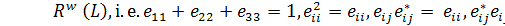 where
where  and
and  , such that
, such that  for all
for all  .
.
Then by [8 , lemma 2.8.2] the set 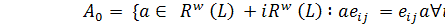 is
a *-subalgebra of
is
a *-subalgebra of  and the map
and the map is a *-isomorphism of M3(Ao)
onto Rw (L) + iRw(L).
is a *-isomorphism of M3(Ao)
onto Rw (L) + iRw(L).
Let
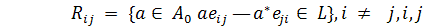 .
.
Note that  , where
, where  and
and  . We prove that
. We prove that  .
.
Let be pairwise distinct indexes in
be pairwise distinct indexes in  . Since
. Since  and
and
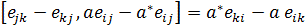
then  . Hence
. Hence  . Therefore
. Therefore  . Also it is easy to see
. Also it is easy to see  .
.
Let  and
and  . Then the elements
. Then the elements  belong to
belong to  and
and
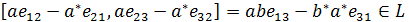
.
Hence  . Therefore
. Therefore  is
a real *-algebra.
is
a real *-algebra.
Let  . Since
. Since  then
then  . It is clear that
. It is clear that
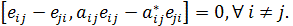
Let  for all
for all  . Then
. Then  consequently multiplying by
consequently multiplying by  and
and 
we get
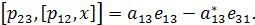
Hence  Analogously we have
Analogously we have  ,
,  . Hence
. Hence  for all
for all  .
.
Conversely, Let  , where
, where  ,
,  . Then we have to show
. Then we have to show  . For the last statement to be proved it
is sufficient to establish
. For the last statement to be proved it
is sufficient to establish  for all
for all  . In turn the last statement is true by
the definition of
. In turn the last statement is true by
the definition of  . Hence
. Hence  . By the last equality L is reversible.
□
. By the last equality L is reversible.
□
3.
The enveloping C*-algebra of a purely real
Lie algebra of
skew-adjoint operators
Theorem 3.1. Let  be
a weakly closed purely real reversible Lie algebra of skew- adjoint operators
on a Hilbert space
be
a weakly closed purely real reversible Lie algebra of skew- adjoint operators
on a Hilbert space 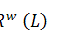 be a real von Neumann algebra, generated by
be a real von Neumann algebra, generated by  in
in
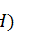 . Suppose that
. Suppose that 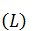 does not have nonzero direct summands of type I. Then
the enveloping C*-algebra
does not have nonzero direct summands of type I. Then
the enveloping C*-algebra 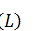 of
of
 is
a von Neumann algebra.
is
a von Neumann algebra.
Proof. By
theorem 1.5 we have  , where
, where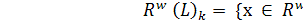 and
and  is
a JW-algebra with no nonzero direct summands of type I.
is
a JW-algebra with no nonzero direct summands of type I.
Let  be
a projection in
be
a projection in  . Then
. Then  is
a JW-algebra with no nonzero direct summands of type I. Hence there exist
pairwise orthogonal and pairwise equivalent by symmetry projections
is
a JW-algebra with no nonzero direct summands of type I. Hence there exist
pairwise orthogonal and pairwise equivalent by symmetry projections  in
in
 such that
such that  . Let
. Let  be partial symmetries in
be partial symmetries in  such that if
such that if  then
then  for all
for all  .
.
Let  and if
and if  then
then  for all
for all  . Then the set
. Then the set  is
a system of matrix units and
is
a system of matrix units and
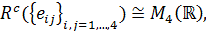
where  is
a real associative algebra, generated by the set
is
a real associative algebra, generated by the set  . At the same time
. At the same time
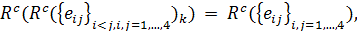
where  is
a real associative algebra, generated by the Lie algebra
is
a real associative algebra, generated by the Lie algebra  . Also, since
. Also, since  we
have
we
have  Hence
Hence  and
and  . Since
. Since  we
have
we
have  . The projection
. The projection  was chosen in
was chosen in  arbitrarily, and a JC-algebra, generated by the set of all
projections of the algebra
arbitrarily, and a JC-algebra, generated by the set of all
projections of the algebra  coincides with
coincides with  . Hence
. Hence
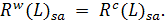
Therefore
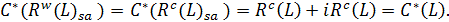
At the same time by  and
and  we
have
we
have
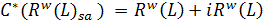
and  is
a von Neumann algebra, i.e.
is
a von Neumann algebra, i.e.  . Hence
. Hence  . □
. □
References
[1] Martindale W.S. III,
Lie isomorphisms of the skew elements of a prime ring with invilution. Commun. Algebra
Vol 4 (1976), P. 929-977.
[2] Rosen M.P. Isomorphisms
of a certain class of prime Lie rings. J. Algebra Vol 89 (1984) 291-317.
[3] Ayupov Sh.A., Azamov N.A. Commutators and Lie isomorphisms of skew elements in prime operator
algebras. Comm. Algebra Vol 24, no 4 (1996),
P. 1501-1520.
[4] Ayupov Sh.A. Anti-automorphisms
of factors and Lie operator algebras. Quart.J.Math., Vol 46 (1995), 129-140.
[5] Ayupov Sh.A. Skew
Commutators and Lie Isimorphisms in Real von Neumann Algebras. J.Funct.Anal.,
Vol 138 (1996), 170-187.
[6] Ayupov Sh.A., Arzikulov F.N. Maximal real von Neumann algebras on a Hilbert space. Uzbek Math. J., No 3 (2006), 7-12.
[7] Arzikulov F.N. On two problems concerning enveloping von Neumann algebras. J. Algebr. Represent Theor. Vol. 14, No. 4 (2011), P. 703-710.
[8] H. Hanche-Olcen, E. St0rmer, Jordan Operator Algebras. Boston
etc: Pitman Publ. Inc., 183, 1984.
[9] E. Kissin, V. S.
Shulman and Yu. V. Turovskii, Banach Lie algebras with Lie subalgebras of finite
codimension: their invariant subspaces and Lie ideals, J. Funct. Anal. 256 (2009),
323-351.
[10] E. Kissin, V. S. Shulman and Yu. V.
Turovskii, Banach Lie algebras with Lie
subalgebras of finite codimension have Lie ideals, J. Lond. Math. Soc. (2), 80 (2009), 603-626.
[11] Li B. Introduction to Operator Algebras. Singapore: World scientific (1992), 237-256.
[12] Stacey P.J. Locally orientable JW-algebras of complex type. Quart. J.Math.-1982.-Vol. 33. No 2, -P. 247-251.
![]() on
a Hilbert space such that
on
a Hilbert space such that ![]() and a real Lie algebra
and a real Lie algebra ![]() of
skew-adjoint operators on a Hilbert space H such that
of
skew-adjoint operators on a Hilbert space H such that ![]() for the real *-algebra
for the real *-algebra ![]() , generated by
, generated by ![]() in
in
![]() . These algebras are called a purely real
von Neumann algebra and a purely real Lie algebra respectively.
. These algebras are called a purely real
von Neumann algebra and a purely real Lie algebra respectively.![]() in B(H) is called a purely real von Neumann algebra if
in B(H) is called a purely real von Neumann algebra if ![]() , where
, where ![]() . Let
. Let ![]() be
the center of
be
the center of ![]() . If
. If ![]() consists of real multiples of 1, i.e.
consists of real multiples of 1, i.e. ![]() , then R is said to be a purely real
factor. Given a purely real von Neumann algebra
, then R is said to be a purely real
factor. Given a purely real von Neumann algebra ![]() it
is easy to see that the set
it
is easy to see that the set ![]() forms a Lie algebra with the multiplication
forms a Lie algebra with the multiplication ![]() . Such Lie algebras and purely real von
Neumann algebras were investigated, in particular, in papers
. Such Lie algebras and purely real von
Neumann algebras were investigated, in particular, in papers ![]() by
Sh.Ayupov. In these papers it was considered a spacial case of a more general
algebraic problem: letting
by
Sh.Ayupov. In these papers it was considered a spacial case of a more general
algebraic problem: letting ![]() and
and ![]() be
simple or prime rings with involutions, can every (Lie) isomorphism of
be
simple or prime rings with involutions, can every (Lie) isomorphism of ![]() onto
onto ![]() be
lifted to an (associative) isomorphism of
be
lifted to an (associative) isomorphism of ![]() onto
onto ![]() ? Here the derived Lie ring
? Here the derived Lie ring ![]() is
the additive span of all commutators
is
the additive span of all commutators ![]() ,where
,where ![]() ; it is a Lie ideal in Lie ring
; it is a Lie ideal in Lie ring ![]() .
.![]() and for arbitrary kind by Rosen
and for arbitrary kind by Rosen ![]() . But in the case of prime rings it is not
possible in general to extend a Lie isomorphism between
. But in the case of prime rings it is not
possible in general to extend a Lie isomorphism between ![]() and
and ![]() to a *-isomorphism between whole
to a *-isomorphism between whole ![]() and
and ![]() . Moreover, there are examples of prime
rings with involution such that
. Moreover, there are examples of prime
rings with involution such that ![]() and
and ![]() are Lie isomorphic but
are Lie isomorphic but ![]() and
and ![]() are not *-isomorphic. Concerning purely real von Neumann algebras
one can see that every purely real von Neumann algebra is semiprime: it is
prime if (but not only if) it is a purely real factor. Examples of simple
purely real factors are given by factors of type
are not *-isomorphic. Concerning purely real von Neumann algebras
one can see that every purely real von Neumann algebra is semiprime: it is
prime if (but not only if) it is a purely real factor. Examples of simple
purely real factors are given by factors of type ![]() (n <
(n < ![]() ),
), ![]() , and à-finite type III [4].
, and à-finite type III [4].![]() it
was proved that if
it
was proved that if ![]() and
and ![]() are real factors not of types
are real factors not of types ![]() and
and ![]() then derived Lie algebras
then derived Lie algebras
![]() and
and ![]() are isomorphic if and only if
are isomorphic if and only if ![]() and
and ![]() are *-isomorphic.
are *-isomorphic.![]() there were proved the following statements: let
there were proved the following statements: let ![]() be
a purely real factor except types
be
a purely real factor except types ![]() and
and ![]() . Then
. Then![]()
![]() , where Rk is the associative
subalgebra generated by
, where Rk is the associative
subalgebra generated by ![]() .
.![]() ,
, ![]() , satisfying the conditions
, satisfying the conditions ![]() ,
, ![]() , where
, where ![]() ,
, ![]() are the real von Neumann subalgebras generated by
are the real von Neumann subalgebras generated by ![]() ,
, ![]() respectively.
respectively.![]() ,
, ![]() . In this paper we give a representation
of all maximal purely real Lie algebras of skew-adjoint elements in the algebra
. In this paper we give a representation
of all maximal purely real Lie algebras of skew-adjoint elements in the algebra
![]() for a complex Hilbert space
for a complex Hilbert space ![]() .
.![]() it
was proved the following theorem.
it
was proved the following theorem.![]() is
isomorphic to the algebra
is
isomorphic to the algebra ![]() , where
, where ![]() and
and ![]() are Hilbert subspaces of
are Hilbert subspaces of ![]() such that
such that ![]()
![]() , the identity elements of the algebras
, the identity elements of the algebras ![]() and
and ![]() are mutually orthogonal and their sum is equal to the
identity element of
are mutually orthogonal and their sum is equal to the
identity element of ![]() , and
, and ![]() and
and ![]() are Hilbert spaces on
are Hilbert spaces on ![]() and
and ![]() respectively such that
respectively such that ![]() , where
, where ![]()
![]() be
an Lie algebra of skew-adjoint operators on a Hilbert space
be
an Lie algebra of skew-adjoint operators on a Hilbert space ![]() . The Lie algebra L is called a purely real Lie algebra, if the real *-algebra
. The Lie algebra L is called a purely real Lie algebra, if the real *-algebra ![]() , generated by
, generated by ![]() in
in
![]() satisfies to the condition
satisfies to the condition ![]() (L) ∩ iR(L) = {0
(L) ∩ iR(L) = {0![]() .
.![]() , where
, where ![]() and
and ![]() are Hilbert subspaces of
are Hilbert subspaces of ![]() such that
such that ![]()
![]() , the identity elements of
, the identity elements of ![]() and
and ![]() are mutually orthogonal and their sum is equal to the
identity element of
are mutually orthogonal and their sum is equal to the
identity element of ![]() , and
, and ![]() ,
, ![]() are Hilbert spaces on
are Hilbert spaces on ![]() and
and ![]() respectively such that
respectively such that![]() , where
, where ![]() .
.