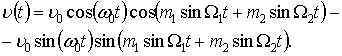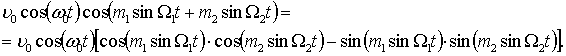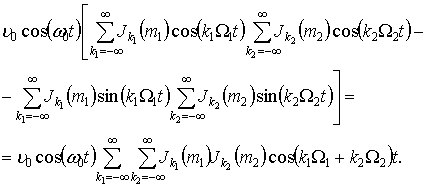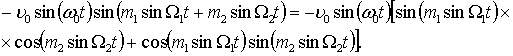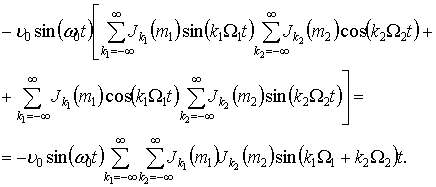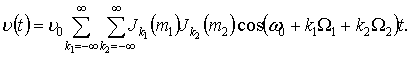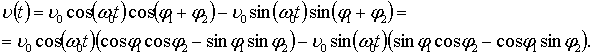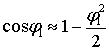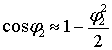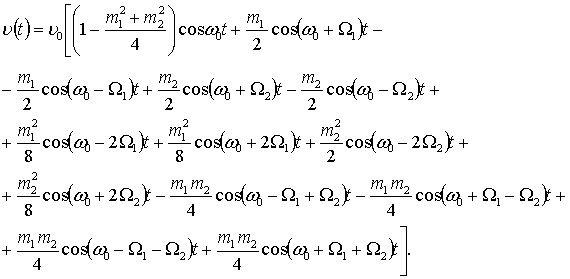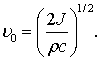Д.т.н., професор В.П. Нагорний
Інститут геофізики ім. С.І. Субботіна НАН України
К.т.н. І.І. Денисюк
Інститут геофізики ім. С.І. Субботіна НАН України
Спектральні
характеристики акустичних хвиль з двотональною кутовою модуляцією
В останні роки
для підвищення дебіту видобувних свердловин широко застосовуються акустичні
методи дії на продуктивні нафтогазоносні пласти. Такими методами обробляють як
привибійні зони пластів так і продуктивний пласт в цілому. При цьому акустичні
хвилі генерують з допомогою спеціальних акустичних випромінювачів і
генераторних пристроїв [1].
Основним
завданням акустичної обробки є підвищення продуктивності видобувних свердловин в
результаті взаємодії хвильових збурень з породою нафтогазонасичених пластів. При
цьому доцільно застосовувати різного виду модульовані акустичні хвилі [2], які
забезпечують широкий частотний діапазон оброблення пластів, на відміну від дії
гармонічної хвилі.
В роботах [3,
4] досліджувались спектральні характеристики модульованих хвиль, коли
модулюючий сигнал змінювався за гармонічною залежністю. З метою розширення
можливостей хвильового впливу на геофізичне середовище пласта проведено
дослідження по визначенню спектральних характеристик акустичних хвиль з двотональною
кутовою модуляцією. Такі хвилі описуються залежністю [5]
|
|
(1) |
,
де 
– висока (несуча)
частота; Ω1, Ω2 – низькі модулюючі частоти; m1, m2 – довільні параметри модуляції; υ – коливальна швидкість частинок середовища.
Співвідношення
(1) подамо у вигляді
|
|
(2) |
Перший член
співвідношення (2) представимо таким чином
|
|
(3) |
Із
урахуванням відомих представлень тригонометричних функцій 
, 
, 
, 
через функції Бесселя першого роду k-го порядку [6] залежність (3) набуває
вигляду
|
|
(4) |
Другий член
співвідношення (2) представимо у вигляді
|
|
(5) |
Співвідношення
(5) виразимо через функції Бесселя
першого роду k-го порядку
|
|
(6) |
Таким чином,
вихідний сигнал (1) з урахуванням співвідношень (4) і (6) має вигляд
|
|
(7) |
Співвідношення
(7) у вигляді подвійної суми являє собою спектр коливань з кутовою модуляцією
для випадку, коли модулюючий сигнал описується двотональним сигналом. Слід
звернути увагу на те, що в спектрі цього сигналу, крім частот 
, 
, 
, 
, …, 
, 
, присутні так звані комбінаційні частоти 
(де 
; 
). Амплітуди цих складових спектра частот залежать від добутку функцій
Бесселя, що є функціями індексів модуляції 
, 
. Підкреслюючи взаємодію окремих складових модулюючого сигналу, кутову
модуляцію, на відміну від амплітудної, інколи називають модуляцією нелінійного
типу [5].
Розглянемо
коливання, що промодульоване двома низькими частотами 
і 
, коли індекси модуляції 
, 
<<1.
При позначеннях
|
|
(8) |
залежність (2) набуває вигляду
|
|
(9) |
Для малих m1, m2 справедливі наближення
|
|
(10) |
Підставивши
співвідношення (10) у вираз (9), після громіздких, проте елементарних
тригонометричних перетворень, вихідний сигнал одержимо у вигляді
|
|
(11) |
Отже, акустичний
сигнал із двотональною кутовою модуляцією при малих значеннях параметрів m1, m2 має в спектральному складі частоти
|
|
|
, 
, 
, 
, 
, 
.
При дії однотонального
сигналу з кутовою модуляцією, коли 
, m1 <<1,
із залежності (11) отримаємо
|
|
(12) |
Із виразу (12)
очевидно, що спектральний склад такої дії звужується до частот 
, 
, 
, 
.
При
проведенні розрахунків за формулою (11) необхідно прийняти вихідні параметри 
, 
, 
, 
сигналу (1) при умові
, 
<<1.
Початкова
амплітуда коливальної швидкості 
розраховується за
формулою [7]
|
|
(13) |
де J – інтенсивність акустичної дії, Вт/м2; ρ – густина породи, кг/м3;
с – швидкість поширення звукової
хвилі в породі, м/с.
Зміщення u часток середовища під дією хвилі з
частотою ω і коливальною
швидкістю υ визначається за
виразом [7]
|
|
(14) |
В якості
прикладу в таблиці приведені, розраховані за формулою (14), амплітуди зміщення
часток середовища при дії сигналу виду (1) на слабонелінійне середовище при
вихідних параметрах: 
м/с; густина
середовища 
кг/м3;
швидкість поздовжніх хвиль в середовищі 
м/с; 
кВт/м2; 
Гц; 
Гц; 
Гц; 
; 
.
Таблиця
Амплітуди
спектральних складових акустичних хвиль з двотональною кутовою модуляцією при 
|
Частота |
Чисельне значення частоти, Гц |
Амплітуда зміщення часток середовища, м |
|
|
9000 |
5,31·10-6 |
|
|
9150 |
2,62·10-7 |
|
|
8850 |
-2,71·10-7 |
|
|
9050 |
2,65·10-7 |
|
|
8950 |
-2,68·10-7 |
|
|
8700 |
6,9·10-9 |
|
|
9300 |
6,45·10-9 |
|
|
8900 |
2,7·10-8 |
|
|
9100 |
6,6·10-9 |
|
|
8900 |
-1,35·10-8 |
|
|
9100 |
-1,32·10-8 |
|
|
8800 |
1,36·10-8 |
|
|
9200 |
1,3·10-8 |
Як видно із
даних таблиці, величини амплітуд зміщення часток середовища малі, порядок їх
складає переважно 10-7, 10-8 м. Відмітимо, що за
результатами натурних вимірів для відчутного впливу на нафтові родовища
достатньо хвильової дії з амплітудою хвиль в межах 10-8…10-9
м [8]. Отже, хвильові дії з амплітудами, приведеними в таблиці, можуть
слугувати спусковим механізмом
вивільнення внутрішньої енергії в пласті в процесі взаємодії хвиль з присутніми
в пласті тріщинами і їх розкриттям, що супроводжується випроміненням хвиль
високої частоти [9]. Відомо також, що при обробці нафт хвилями високої частоти
знижується їх в’язкість [10], в результаті чого підвищується рухливість нафт в
каналах фільтрації пласта, що сприяє підвищенню припливу нафти на вибій
свердловини і підвищенню її дебіту.
Висновки.
Отже, при дії
на геофізичне середовище акустичних хвиль з двотональною кутовою модуляцією випромінюються
коливання з частотами 
, 
, 
, 
, 
, 
, що дозволяє обробляти середовище з достатньо широким
частотним спектром. Отриманий результат може бути використаний в процесі
обробки нафтових покладів акустичними хвилями з двотональною кутовою модуляцією
з метою підвищення продуктивності нафтовидобувних свердловин.
Література
1.
Развитие опыта акустической обработки продуктивной зоны
скважин / В. Александров, М. Бушер, Ю. Казаков, В. Майоров //
Технологии ТЭК. – 2003. – № 2. – С. 1–9.
2.
Островский
Л.А. Введение в теорию модулированных волн / Л.А. Островский, А.И. Потапов. – М.: Физматлит, 2003. – 400 с.
3.
Нагорний В.П. Спектральні характеристики хвиль, збуджених
фазово-модульованим акустичним сигналом в нелінійному геофізичному середовищі /
Нагорний В.П., Денисюк І.І., Юшицина Я.О. // Геоінформатика. – 2014. – № 2
(50). – С. 65–68.
4.
Нагорний В.П. Перспективи застосування амплітудно-модульованих хвиль для
підвищення дебіту видобувних свердловин / Нагорний В.П., Денисюк І.І., Ліхван
В.М. // Нафтогазова галузь України. – 2014. – № 5. – С. 22–26.
5.
Баскаков С.И. Радиотехнические
цепи и сигналы / С.И. Баскаков. – М.: Высшая школа, 1988. –
448 с.
6.
Справочник
по специальным функциям / Под ред. М. Абрамовица, И. Стиган. – М.: Наука,
1979. – 830 с.
7.
Нагорний В.П., Денисюк І.І. Імпульсні методи
інтенсифікації видобутку вуглеводнів. – К.: Ессе, 2012. – 323 с.
8.
Курленя М.В., Сердюков С.В. Определение области вибросейсмического воздействия
на месторождение нефти с дневной поверхности // ФТРПИ. – 1999. – № 4. – С. 4–11.
9.
Партон В.З.
Механика разрушения: от
теории к практике. – М.: Наука, 1990. – 240 с.
10.
Нагорный
В.П., Денисюк И.И., Лихван В.М., Швейкина Т.А. Исследование повышения
эффективности пузырькового режима течения флюидов // Нефтяное хозяйство, 2013.
– № 5. – С. 80–82.