Аширбаев
Х.А., Джумагалиева А.И., Балабекова М.О.
Южно-Казахстанский
государственный университет им. М.О. Ауезова
ПУЛЬСАЦИОННЫЕ
ХАРАКТЕРИСТИКИ ГАЗОЖИДКОСТНОГО СЛОЯ НА КРУПНОПЕРФОРИРОВАННОЙ ПРОТИВОТОЧНОЙ
ТАРЕЛКЕ.
Пульсация газожидкостного слоя
Рассмотрим следующую
модель пульсирующего газожидкостного слоя на крупноперфорированной
противоточной тарелке (рисунок 1), в которой точка 0,
соответствует равновесному положению верхней границы газа газожидкостного слоя. Изменение верхней границы слоя от
равновесного положения определяется координатой у, которое является следствием
неоднородности среды и пульсирующего давления за счет вихреобразования в
газовой каверне [1-4]. Локальными флуктуациями
поверхностного слоя пренебрегаем.
Тогда мгновенное значение полной динамической высоты
газожидкостного слоя равно (рисунок 1).
![]() (1)
(1)
где ![]() статическая высота газожидкостного слоя, равная среднему значению
высоты пульсирующего газожидкостного слоя;
статическая высота газожидкостного слоя, равная среднему значению
высоты пульсирующего газожидкостного слоя;
у - часть пульсирующей слагаемой, зависящая от неоднородности
газожидкостного слоя, т.е. от динамического состояния;
у1 - часть пульсирующей слагаемой,
зависящая от частоты вихреобразования в газовой каверне.
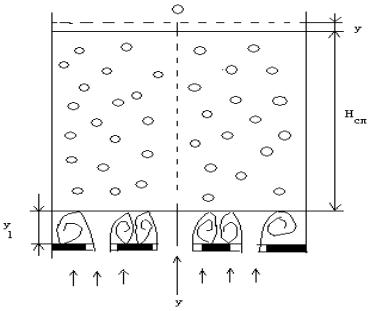
Рисунок 1
Колебание поверхности газовой камеры, непосредственно
связано с частотой вихреобразования. Упрощая задачу, придадим этому колебанию
синусоидальной закон [5]:
![]() (2)
(2)
где Ак- максимальное значение
амплитуды колебаний поверхности газовой каверны;
![]() - частота вихреобразования;
- частота вихреобразования; ![]() время.
время.
На пульсирующий газожидкостный слой действуют следующие
силы: сила тяжести ![]() , сила упругости газожидкостной среды
, сила упругости газожидкостной среды ![]() , противодействующая неоднородности среды и ее
деформации, и сила сопротивления
, противодействующая неоднородности среды и ее
деформации, и сила сопротивления ![]() , стремящаяся гасить любые изменения пульсации слоя.
, стремящаяся гасить любые изменения пульсации слоя.
Составляем дифференциальное уравнение движения верхней
границы газожидкостного слоя действием сил ![]() и
и ![]() :
:
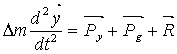 ,
(3)
,
(3)
где ![]() -масса пульсирующего слоя.
-масса пульсирующего слоя.
Определим проекции сил ![]()
![]() и
и ![]() на ось у. Проеция силы
на ось у. Проеция силы ![]() на ось у, равна
на ось у, равна
![]() (4)
(4)
где ![]() - коэффицент
пропорциональности, которой находится из условия разрешимости полученного
дифференциального уравнения.
- коэффицент
пропорциональности, которой находится из условия разрешимости полученного
дифференциального уравнения.
Проекция силы сопротивления ![]() на ось у,
пропорциональна скорости пульсации поверхности слоя в сечении аппарата:
на ось у,
пропорциональна скорости пульсации поверхности слоя в сечении аппарата:
![]() (5)
(5)
где ![]() - коэффициент сопротивления среды, зависящий от внутренных и
внешних факторов, его размерность
- коэффициент сопротивления среды, зависящий от внутренных и
внешних факторов, его размерность 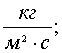
![]() - площадь поперечного сечения аппарата.
- площадь поперечного сечения аппарата.
Проекция
силы тяжести ![]() на ось у равна
на ось у равна
![]() (6)
(6)
где ![]() -масса газожидкостного слоя.
-масса газожидкостного слоя.
Масса
газожидкостного слоя:
![]() (7)
(7)
Массу пульсирующего слоя
считаем пропорциональной общей массе газожидкостного, и поэтому
![]() (8)
(8)
где, к-коэффициент
пропорциональности, показывающий долю пульсирующей части всей массы жидкости.
Среднее значение высоты газожидкостного слоя [6-8]
![]() (9)
(9)
где ![]() -газосодержание.
-газосодержание.
С учетом (2), (4)-(9) уравнение движение верхней границы газожидкостного
слоя (3) в направлении "у"
имеет вид:
![]()
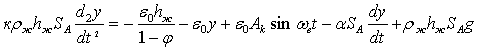 (10)
(10)
Сокращая обе части уравнения (10) на величину ![]() и после некоторых
преобразований, получим:
и после некоторых
преобразований, получим:
![]() (11)
(11)
Для решения дифференциального уравнения (11) должно
соблюдаться следующее условие:
![]() (12)
(12)
Откуда ![]() (13)
(13)
Подставляя значение ![]() из равенства (13) в
уравнение (11), получим
из равенства (13) в
уравнение (11), получим
![]() (14)
(14)
Принимая
общеизвестные обозначения:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
приведем уравнение (14) к относительному виду:
![]()
![]() (18)
(18)
Полученное выражение представляет собой дифференциальное
уравнение вынужденных колебаний при наличии сопротивления среды,
пропорциональной скорости пульсации.
Как известно, решение уравнения (18) равно сумме общего
решения однородного уравнения и частного решения неоднородного уравнения. В
аппарате практический интерес представляет установившейся процесс, т.е. частное
решение неоднородного уравнения (18), которое имеет вид
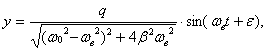 (19)
(19)
где ![]() -сдвиг фазы колебаний относительно фазы возмущающей силы,
которой определяется по формуле
-сдвиг фазы колебаний относительно фазы возмущающей силы,
которой определяется по формуле
![]() (20)
(20)
В установившемся режиме вынужденные колебания
газожидкостного слоя приисходят с частотой вихреобразования и являются
гармоническими; амплитуда и фаза колебаний также зависят от ![]()
Амплитуда
вынужденных колебаний газожидкостного слоя для установившегося движения равна [9]
 (21)
(21)
Решая
уравнение (21) относительно частоты ![]() вихреобразования,
получим:
вихреобразования,
получим:
 (22)
(22)
Уравнение (22) имеет вещественное решение при соблюдении
следующего условия:
![]() (23)
(23)
Из равенства (23) получим минимальное значение собственной
частоты газожидкостного слоя
 (24)
(24)
С учетом (15) и (17) уравнение (24) примет вид:
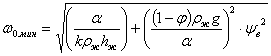 (25)
(25)
где ![]() -функция, зависящая
от параметров вихреобразования.
-функция, зависящая
от параметров вихреобразования.
Учитывая, что ![]() получим
получим
 (26)
(26)
Исследование функции ![]() показывает, что
частота слоя имеет минимальное значение, если
показывает, что
частота слоя имеет минимальное значение, если ![]() равен
равен
![]() (27)
(27)
Зависимость частоты
пульсаций газожидкостного
слоя от скортости газа в
колонне
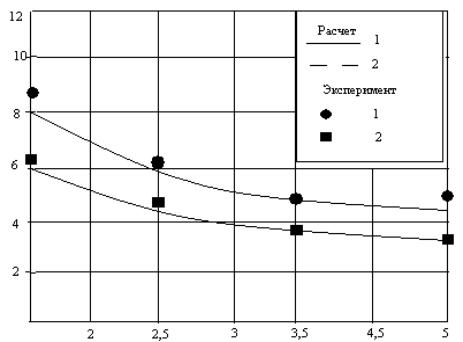
Ось
абсцисс – скорость газа в колонне
![]() , ось ординат –частота пульсаций газожидкостного слоя (fсл, с-1). Sап=0.225м2 ; S0=0.19782 м2/м2; d0=0,06м. Обозначения
экспериментальных точек 2 и
кривых, построенных по уравнению (28)
1-U=4·78·10-3
, ось ординат –частота пульсаций газожидкостного слоя (fсл, с-1). Sап=0.225м2 ; S0=0.19782 м2/м2; d0=0,06м. Обозначения
экспериментальных точек 2 и
кривых, построенных по уравнению (28)
1-U=4·78·10-3 ![]() ; 2-U=6.94·10-3
; 2-U=6.94·10-3![]()
Рисунок 2
С учетом (27) значение
минимальной частоты пульсаций слоя примет, следующий вид:
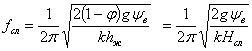 (28)
(28)
На рисунке (2) представлен график зависимости ![]() при различных
плотностях орошения. Как видно, полученное уравнение (28) адекватно описывает
характер снижения частоты пульсаций слоя с повышением скорости газа в колонне.
При повышении потностей орошения характер снижения не изменяется. Погрешность составляет
не более 11%.
при различных
плотностях орошения. Как видно, полученное уравнение (28) адекватно описывает
характер снижения частоты пульсаций слоя с повышением скорости газа в колонне.
При повышении потностей орошения характер снижения не изменяется. Погрешность составляет
не более 11%.
Список использованных источников.
1.Тапалов Т.Т. Структура
потоков и массобмен на крупнодырчатой повальной тарелке промышленных размеров.:
Дис...канд.тех.наук.-М., 1983.-180с.
2.Теория турбулентных
струй . Под ред. Г.Н.Абрамовича.-М.: Наука, 1984-716с.
3. Zh. Serikuly, A.A. Volnenko, Ya. Kenig. Hydrodynamics of
apparatuses with preformed packing bodies // The 7th International
Conference Interdisciplinarity in Engineering (INTER-ENG 2013). Procedia Technology 12 (2014), P.375-381.
4. Волненко А.А., Мавиди Л.Х., Алтухов А.В., Бажиров Т.С. Применение
системно-поэлементной методологии для модернизации фильтровального оборудования
в схеме переработки попутного нефтяного газа // Тр.межд.науч.-практ.конф. «Ауэзовские чтения-12»: «Роль регионального
университета в развитии инновационных направлений науки, образования и
культуры», Шымкент, 2014, Т.1.- С.80-84.
5. Мавиди
Л.Х., Волненко А.А. Гидравлическое сопротивление при фильтрации потока через
сетчатые фильтрующие элементы // Вестник МКТУ им.
Х.А.Ясави.- 2014, №1(88). - С. 111- 115.
6. Волненко
А.А., Балабеков О.С., Алтухов А.В., Бажиров Т.С., Серикулы Ж., Сарсенбекулы Д. Изучение
основных параметров работы сушильного и газоочистного оборудования //
Химический журнал Казахстана, №2(46), 2014.- С.331-343
7. Волненко А.А., Балабеков О.С.,
Алтухов А.В., Бажиров Т.С., Абжапбаров А.А. Моделирование и оптимизация
процесса сушки в барабанном аппарате с различной насадкой //
Химический журнал Казахстана, №2(46), 2014.- С.372-379
8. Volnenko A., Serikuly Zh.,
Sarsenbekuly D., Kumisbekov S. Mass transfer coefficients in a gas phase in
volume of a regular nozzle with drop structure of a gas – liquid stratum // Life
Science Journal, 11(9), 2014, P. 488- 492.
9. Serikuly Zh., Volnenko A., Kumisbekov S. Mass transfer
in the apparatuses with preformed packing bodies // International Review of
Mechanical Engineering (IREME), Vol.8, №4, 2014.- P. 779 – 784.
![]()