К.т.н. Дорошенко О.І., Борисенко С.О.

Одеський національний політехнічний університет, Україна

ВАТ “Одесаобленерго”, Україна

ПРО ОПТИМАЛНЕ РЕАКТИВНЕ НАВАНТАЖЕННЯ СИСТЕМ

ЕЛЕКТРОПОСТАЧАННЯ СПОЖИВАЧІВ ЕЛЕКТРОЕНЕРГІЇ

Зважаючи на [1], можна стверджувати, що система електропостачання (СЕП) конкретному споживачеві є підсистемою загальної електроенергетичної системи (ЕЕС), а його спожита у розрахунковому періоді електроенергія (ЕЕ), фізично, є енергією електромагнітного поля такої системи і передається за допомогою електропружного діелектричного середовища, що оточує усі струмоведучі частини таких систем. При цьому, у відповідності до реально-математичної моделі таких систем, енергію їх полів умовно розкладають на дві складові: активну (електричне поле) і реактивну (магнітне поле). При цьому, нормативний документ [2], що діє до тепер в Україні, визначає енергію електромагнітного поля як “особливий вид матерії”, що суперечить її філософському розумінню. Тому в роботах [3 – 6] запропоновано її визначення як “особливий стан матеріального середовища, у якому під дією зовнішніх чинників починають діяти сили”. При цьому в електричному полі діють електричні сили (сили Кулона), а в магнітному полі – механічні сили (сили Кариоліса).

Повну потужність електромагнітного поля СЕП визначають за відомою формулою, кВА

, (1)

де - діюче значення напруги струмоведучих частин СЕП, кВ; - діюче значення струму провідності струмоведучих частин СЕП, А; - кут зсуву фаз згаданих напруги і стуму, град.

Спираючись на фізику [7] і на теорему Пойтинга, в роботі [8] відому формулу визначення повної потужності електромагнітного поля системи названо його реально-математично моделлю.

Графічно, залежність (1) наведено на рис.1. Як можна бачити, енергія електричної частини електромагнітного поля СЕП незмінна за часом (діюче значення) і перетворюється електроприймачами системи у інші види (споживається) для виконання ними корисної роботи. Її називають активною енергією системи.

Рис.1. Реально-математична модель потужності електромагнітного поля СЕП споживача ЕЕ

Це поздовжня складова енергії електромагнітного поля системи (до напрямку електропередачі). Енергія магнітної частини електромагнітного поля СЕП змінюється за часом з подвійною частотою зміни напруги. Як доведено в [8], її загальне значення протягом періоду зміни напруги дорівнює нулю. Тобто, ні до електроприймачів, ні від них вона не

передається. Це внутрішня енергія системи, яка не приймає корисної участі у процесах електроспоживання. Це поперечна складова енергії електромагнітного поля системи (до напрямку електропередачі). Через явище електромагнітної індукції, вона повертається до середовища струмоведучих частин системи, створюючи електрорушійну силу (ЕРС) самоіндукції і струм самоіндукції, напрямок якого завжди протилежний до напрямку струму від джерела живлення. Саме тому цю складову енергії поля системи називають реактивною.

Реактивний струм струмоведучих частин СЕП (їх струм самоіндукції) збільшує їх активні втрати, зменшує пропускну спроможність (їх переріз визначається допустимим струмом) та суттєво впливає на рівень напруги. Тому величину реактивного навантаження СЕП конкретним споживачам потребує нормування, що вимагають усі нормативні документи, які діють в електропостачанні.

У якості норми реактивного навантаження споживачів доцільно застосовувати значення коефіцієнта реактивної потужності, який визначається за відомою формулою, в.о.

, (2)

де - значення реактивної енергії СЕП споживача у розрахунковому періоді, зафіксоване комерційним обліком електроенергії, квар·год.; - значення активної енергії СЕП споживача у розрахунковому періоді, зафіксоване комерційним обліком електроенергії, кВт·год.

Приймаючи до уваги формулу (1) і, зважаючи на рис.1 можна зробити наступний висновок – добуток діючих значень напруги і струму провідності струмоведучих частин при визначенні активної потужності (енергії) СЕП є величиною середньою за період їх зміни (діюче значення), а їх добуток при визначенні реактивної потужності (енергії) СЕП є величиною амплітудною за період їх зміни. Тому для визначення директивного значення, формулу (2) необхідно представити у вигляді, в.о.

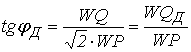. (3)

Як відомо активні втрати в струмоведучих частинах СЕП можна визначати за відомою формулою, кВт

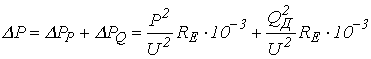, (4)

де - активні втрати в струмоведучих частинах СЕП тільки від її активного навантаження, кВт; - активні втрати в струмоведучих частинах СЕП тільки від її реактивного навантаження, кВт; - середнє активне навантаження споживача у розрахунковому періоді, кВт; - середнє (діюче) значення реактивного навантаження споживача у розрахунковому періоді, квар; - еквівалентний активний опір струмоведучих частин СЕП, приведений до номінальної напруги джерела її живлення, Ом

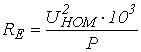. (5)

Приймаючи за умовну одиницю , рівняння (4) у відносних одиницях можна представити у вигляді, в.о.

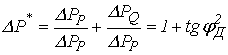. (6)

Для СЕП конкретного споживача ЕЕ формула (6) набуває вигляду;

Для директивного значення його реактивної потужності, в.о.

, (7)

де - директивна величина значення коефіцієнта реактивної потужності, що відповідає його діючому реактивному навантаженню, в.о.

Для розрахункового значення його коефіцієнта реактивної потужності у розрахунковому періоді, в,о.

, (8)

де - розрахункова величина значення коефіцієнта реактивної потужності, що відповідає його діючому реактивному навантаженню у розрахунковому періоді, в.о.

Збиток споживача від активних втрат, обумовлених реактивним навантаженням у розрахунковому періоді, можна представити у вигляді, в.о.

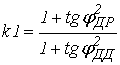. (9)

Зважаючи на те, що переріз струмоведучих частин СЕП вибирають за їх повним розрахунковим струмом провідності, можна вважати, що , де

. (10)

За незмінного значення , яке не перебільшує його договірного значення, рівняння (10) можна представити у вигляді, в.о.

. (11)

За аналогією з формулою (9), збиток споживача від зменшення пропускної спроможності струмоведучих частин його СЕП, обумовлених реактивним навантаженням у розрахунковому періоді, можна представити у вигляді, в.о.

. (12)

Загальний збиток споживача за розрахункового значення коефіцієнта його реактивного навантаження можна визначити за формулою, в.о.

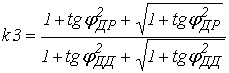. (13)

Графік залежностей за формулами (9), (12) та (13) наведено на рис.2.

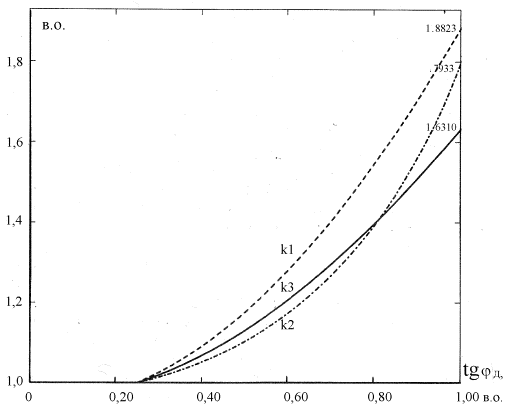
Рис.2. Графік залежності , та

Таким чином, плату споживача за активне електроспоживання, яке пов’язується тільки з його активним навантаженням можна визначити, грн.

, (14)

де - плата споживача за його активне електроспоживання, зафіксоване комерційним обліком у розрахунковому періоді, грн.

Плату споживача за активне електроспоживання, яке пов’язується тільки з його реактивним навантаженням можна визначити, грн.

. (15)

У якості прикладу розглянемо СЕП споживача, принципову схему якого наведено на рис.3.

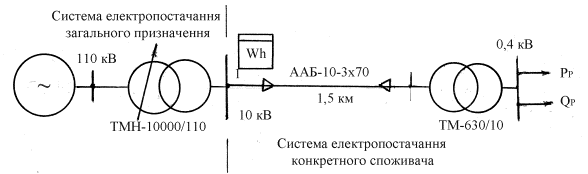
Рис.3. Принципова схема СЕП реального споживача ЕЕ.

Як можна бачити, він живиться від ЕЕС при напрузі кВ і його комерційний облік ЕЕ розташується у точці розподілу балансової належності електричних мереж споживача і електропостачальної організації – 1.

На протязі минулого року облік зафіксував такі значення витоку ЕЕ:

Активної – кВт·год.

Реактивної – квар·год.

Вартість активного електроспоживання склала – грн.

Зважаючи на те, що електрична енергія передається споживачеві у потенційному вигляді – у вигляді напруги, схему заміщення його СЕП можна представити у вигляді рис. 4.

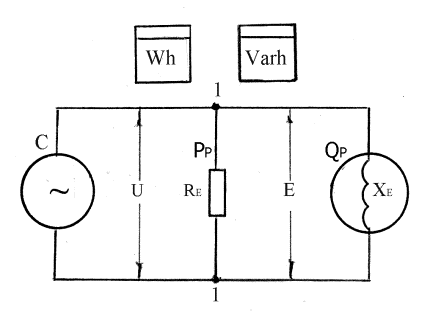
Рис.4. Заступна розрахункова схема СЕП споживача.

При цьому, коефіцієнт реактивної потужності складає величину:

Амплітудне значення

в.о.

Діюче значення

в.о.

Якщо директивне значення коефіцієнта реактивної потужності споживачеві установлено на рівні в.о., до за формулою (13)

в.о.

Плата споживача за активне електроспоживання протягом року, яке пов’язується тільки з його активним навантаженням можна визначити за формулою (14)

грн.

Плата споживача за активне електроспоживання протягом року, яке пов’язується тільки з його реактивним навантаженням можна визначити за формулою (15)

грн.

Висновок:

За кошти, що дорівнюють збитку конкретного споживача ЕЕ протягом року від власного реактивного навантаження, можна придбати регульовану конденсаторну установку з конденсаторами 0,4 кВ, яка суттєво зменшить його збиток і збиток електропостачальної організації [9].

Література

1. Бессонов Л.А. Теоретические основы электротехники / Л.А. Бессонов Изд. 6-е. Учебник для студ. энергетич. и электротехнич. вузов. – М.: Высш. школа, 1973. – 752 с.

2. ДСТУ 2843–94. Державний стандарт України. Електротехніка. Основні поняття. Терміни та визначення. Київ: Держстандарт України, 1995. – 66 с.

3. Дорошенко О.І. Щодо питання матеріальності в фізиці електроенергетики / О.І. Дорошенко // Наукові праці Донецького національного технічного університету. Випуск 11 (186), Донецьк – 2011. – С. 120 – 124.

4. Дорошенко О.І. Про фізику електромагнітного поля електроенергетичної системи /О.І. Дорошенко // Матеріали ХІ міжнародної науков-технічної конференції “Фізичні процеси та поля технічних і біологічних об’єктів ” – Кременчук, 2 – 4 листопада 2012 р. – С. 33 – 35.

5. Дорошенко О.І. Фізичні основи електромагнітного поля електроенергетичної системи. / О.І. Дорошенко, О.В. Панчишин, І.,В. Касаткіна // Матеріали ХІІ Міжнародної науково-технічної конференції “Фізичні процеси та поля технічних і біологічних об’єктів. Кременчук, 8 – 10 листопада 2013 р. – С. 15 – 17.

6. Дорошенко О.І. Про фізику електричної енергії електроенергетичної системи / О.І. Дорошенко // Матеріали ХІІІ Міжнародної науково-технічної конференції “Фізичні процеси та поля технічних і біологічних об’єктів. Кременчук, 09 – 11 листопада 2014 р. – С. 22 – 24.

7. Ландау Л.Д. Курс общей физики. Механика и молекулярная физика / Л. Д. Ландау, А.И. Ахиезер, Е.М. Лифшиц. // М.: Изд. «Наука», Главная редакция физико-математической литературы.– 1969. – 399 с.

8. Дорошенко О.І. Про математику і фізику електропередачі. / О.І. Дорошенко // Матеріали Х-ої міжнародної науково-практичної інтернет-конференції “Новини наукової думки” 27 жовтня – 05 листопада 2014 р., Прага. – С. 15 – 22.

9. Зубюк Ю.П. Сучасні конденсатори в системах електропостачання. / Ю.П. Зубюк // Промелектро, 2004. – № 6. – С. 53 – 55.