Экономические науки/ 8.Математические методы в экономике

Мальков О.В.,

аспірант ДВНЗ «Київський національний економічний університет ім. Вадима Гетьмана»

Моделювання ефективності праці ІТ-фахівців аутсорсингового підприємства

Для дослідження якості роботи ІТ-фахівців дослідимо статистичні дані реакції на заявку і вирішення проблеми [1]. Введемо параметр – часовий проміжок від одержання заявки до вирішення проблеми (год).

Дослідимо для аутсорсингового підприємства, що працює в полі ринкових відносин ІТ-послуг. Для цього проаналізуємо інтервальний статистичний розподіл вибірки для аутсорсинсового підприємства з обсягом вибірки 11013. Одержано основні числові характеристики дискретного розподілу часових проміжків від одержання заявки до вирішення проблеми: Середнє вибіркове – 4,93; Дисперсія – 6,67, Середнє квадратичне відхилення – 2,59, Асиметрія – 1,09, Ексцес – 3,91. На Рис.3 представлено графік відносних частот і підбір закону розподілу. За формою графіків відносних частот можемо припустити, що величина має -розподіл Пірсона, за умови зсуву графіка відносних частот часового проміжку від одержання заявки до вирішення проблеми на один інтервал вліво. Таким чином, висувається нульова гіпотеза : ознака зі зсувом на один інтервал може бути представлена у вигляді -розподілу Пірсона.

Відомо, що функція -розподілу дорівнює [2, с. 244]:

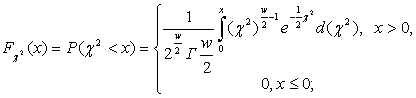(1)

де – число ступенів свободи.

Для -розподілу функція щільності ймовірності знаходиться у вигляді:

.

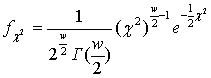Розподіл статистики , називається -розподілом Пірсона. Для перевірки правильності використаємо критерій узгодженості Колмогорова з рівнем значущості =0,01. Графічно та чисельно визначимо , яке б задовольняло нерівність

₍₄₎

та перевіримо правильність висунутої нульової гіпотези.

Обсяг вибірки 11013, тоді знаходимо:

₍₅₎

Отже, за критерієм узгодженості 0,67<0,76 – гіпотеза приймається

Таким чином, висунута гіпотеза підтверджується і ознаку представити у вигляді -розподілу Пірсона.

Після дослідження за критерієм Колмогорова правильності гіпотези, функцію щільності ймовірності - розподілу необхідно зсунути вправо по осі абсцис (Рис.5).

Рис. 2. Ілюстрація чисельного розв’язку зсуву функції щільності ймовірності -розподілу до графіка відносних частот

З Рис.5 видно, що найкращий результат досягається, коли , якщо область визначення : .

Знаходимо аналітичний вираз щільності ймовірності – розподілу:

_.

Таким чином, знайдено середнє значення (год) від одержання заявки до вирішення проблеми для аутсорсингового підприємства. Отже, запропоновано підходи до оцінювання показників аутсорсингового підприємства, серед яких є підхід оцінювання якості роботи ІТ-фахівців.

Література.

1. Oren T. I. Concepts for Advanced Simulation Methodologies,

Simulation / T. I. Oren, B. P. Zeigler. – North-Holland Publishing

company, pp. 78 – 88, 2009.

2. Блудова Т. В. Теорія ймовірностей : Навч. посіб. для студ. вищ. навч. закл. / Т. В. Блудова; ред.: В. С. Мартиненко; НБУ. Львів. банк. ін-т. - Л. : ЛБІ НБУ, 2005. - 318 c.