Технические
науки / Водоснабжение и водоотведение
Алгоритм расчета характеристик
сложных гидравлических систем
Гусенцова Я.А.1, Коваленко А.А2, Риблова Е.В.1
Луганский национальный
аграрный университет1
г. Луганск, городок
Луганского национального университета, 91008
Луганский
государственный университет имени В.
Даля2
г Луганск, квартал
Молодежный 20 а, 910342
THE ALGORITHM FOR CALCULATING THE CHARACTERISTICS OF COMPLEX HYDRAULIC
SYSTEMS
Gusentsova Y.A.1, Kovalenko A.A.2, Riblova E.V.1
Lugansk National Agrarian University1
Lugansk, Lugansk National University campus, 91008
Lugansk State University named after V. Dahl2
Lugansk, Molodejni 20a, 910 342
Аннотация. Приведена математическая модель и алгоритм расчета
характеристик сложной гидравлической системы. Показано, что ее использование
позволило снизить приведенные затраты системы водоснабжения городского квартала
на 18%.
Ключевые слова. Математическая модель, гидравлическая система, алгоритм,
приведенные затраты, оптимизация
Summary. The mathematical model and algorithm of calculation of complex
hydraulic systems characteristics are presented. It is shown that its use has
allowed to reduce the adjusted cost system of water supply of the city quarter
by 18%.
Key words. Mathematical model,
hydraulic system, algorithm, reduced costs, optimized
Коммунальные и промышленные предприятия различных отраслей
промышленности (химической, нефтехимической, минеральных удобрений, металлургии
черных и цветных металлов, целлюлозной и лесохимической, строительных
материалов, пищевой, химико-фармацевтической и др.) являются крупнейшими
потребителями водных ресурсов, используемых для производства промежуточных и
конечных продуктов.
Сокращение потребления топливно-энергетических ресурсов в
промышленности сопряжено с широкомасштабной реализацией современных
энергосберегающих технологий, созданием высокоэффективных энерготехнологических
комплексов. Процессы в системах водоснабжения характеризуются сравнительной
сложностью. Вследствие этого для получения наибольшего эффекта при модернизации
действующих и вновь проектируемых систем необходимо в полной мере использовать
методы системного анализа [1,2].
Среди всех факторов и мероприятий интенсификации систем
водоснабжения особую роль играют
эффекты, связанные с оптимальным выбором структуры и элементов системы. Опыт
показывает, что экономический эффект от оптимальной структуры системы примерно
на порядок выше эффектов от оптимальной организации отдельных элементов или
оптимального управления процессом. Реализация этих эффектов достигается не
только при создании новых систем, но и при реконструкции действующих.
Обзор методов и
алгоритмов их синтеза показал, что различают синтез: альтернативных вариантов систем,
систем в стадии эскизного проекта проектируемой системы, схемы системы в связи
с интенсификацией или ее реконструкцией. Одним из основных затруднений при
поиске оптимальной системы для задач промышленного масштаба является
комбинаторная проблема, т.е. огромное число возможных вариантов. Такое обилие
альтернативных вариантов в свою очередь порождает многочисленные принципы и
подходы к анализу и синтезу систем водоснабжения, среди которых можно выделить
два направления. Первое направление основано на поиске оптимальной системы
строгими алгоритмическими методами с решением сложных оптимизационных задач.
Второе связано с использованием разных эвристических методов. Оба направления
обладают рядом недостатков [3,6].
Существуют и различные комбинации рассмотренных методов.
После синтеза структуры системы приступают к построению ее математической
модели. Математическая модель представляет собой систему уравнений
математического описания, отражающую сущность явлений, протекающих в объекте
моделирования, которая с помощью определенного алгоритма позволяет
прогнозировать поведение объекта при изменении входных и управляющих
параметров.
После этого можно
рассчитать эффективные показатели различных элементов системы.
Выделяют несколько видов показателей эффективности:
экономические, экологические, надежность и экологическая безопасность, простота
контроля и управления, гибкость.
Некоторые показатели эффективности, например, экономические
и экологические, можно точно рассчитать. Другие, например, сложность, гибкость
– нельзя. В этом случае необходимо использовать экспертные оценки
проектировщиков.
Вычисляемые показатели можно определить с помощью
математической модели. Отсюда следует насколько важно иметь такую модель
системы, которая позволяет, не затрагивая сами процессы, определить, какое
решение нужно принять, чтобы улучшить ее показатели [5,7,8].
Задача оптимизации системы водоснабжения – это задача
внесения изменений в исходный проект для улучшения его экономических
показателей.
В представленной работе
рассматривается задача рационального выбора
параметров сложных гидравлических систем.
Постановка задачи
оптимизации
Необходимо разработать математическую модель и
алгоритм расчета характеристик сложной гидравлической системы, на основании
которой определить ее рациональные
параметры сточки зрения экономической эффективности.
Для этого должна быть задана схема системы с
указанием расстояний между точками отбора, давления в точках отбора. Параметрами оптимизации являются диаметры
труб. Целевой функцией являются приведенные затраты, которые складываются из
стоимости труб и стоимости электроэнергии за год эксплуатации трубопровода.
Стоимость труб рассчитывается как
,
где
- длина участка между узлами 
и 
, 
- диаметр трубы на этом участке, и 
- стоимость одного метра трубы с диаметром 
.
Статистический анализ различных производителей показал, что зависимость цены одного метра трубопровода от диаметра хорошо описываются линейной
функцией, что позволяет находить стоимость труб для любого диаметра.
Стоимость электроэнергии рассчитывалась как
,
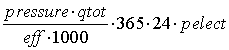где
- давление,
создаваемое насосом, 
- полный расход на выходе насоса,
- коэффициент полезного действия насоса; 
- цена одного киловатт-часа электроэнергии Тогда полные
приведенные затраты 
можно рассчитать как
сумму этих затрат
.
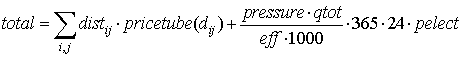Алгоритм оптимизации
1.
Ввод исходных данных.
Ввод исходных данных осуществляется с помощью
программы init. Вводится матрица связей С, число узлов схемы 
, вектор величин расходов в узлах 
, матрица расстояний dist, зависимость цены труб от диаметра и набор
стандартных значений диаметров труб.
Матрица связей определяется следующим
образом. Ее элементы 
отличны от нуля только в том случае, когда между узлами 
и 
существует связь, т.е. они соединены трубопроводом. Причем 
если поток направлен
от узла 
к узлу 
и 
в противном случае. Размерность матрицы связей равна 
. Заполнение матрицы проводится в порядке возрастания номера
узла. Причем достаточно ввести только положительные связи, а затем провести
антисимметризацию матрицы. Если окажется, что знак какого-либо элемента выбран
неправильно, в решении системы уравнений соответствующий поток окажется
отрицательным.
Вектор 
(расход на выходе) имеет
размерность 
и его элемент 
дает величину расхода
в узле с номером 
. Матрица расстояний dist представляет собой симметричную матрицу
размером 
, элемент 
которой дает расстояние (длину трубопровода) между узлами с
номерами 
и 
. Проводится симметризация матрицы.
2.
Составление уравнений
неразрывности для узлов.
Для узла с номером 
формируется вектор
всех его связей 
. Он представляет собой 
- строку матрицы С. Затем составляется уравнение
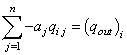. (1)
3.
Составление списка
неизвестных расходов.
Для составления списка неизвестных расходов
определяются индексы ненулевых элементов матрицы связей. Знак расхода
определяется знаком соответствующего элемента матрицы С. Поэтому необходимо
искать только величину расхода. Расходы 
и 
имеют одинаковую
величину (модуль). Чтобы учесть это обстоятельство в списке неизвестных расходов
проводится замена 
при условии, что 
.
4.
Решение системы
уравнений для потоков.
В системе число уравнений для расходов равно числу неизвестных. Это дает
возможность решения полученной системы уравнений без привлечения дополнительных
уравнений для давлений.
5.
Создание целевой
функции.
Так как расходы известны, можно составить
уравнения для давлений и решить их независимо. По известным давлениям находится
давление насоса, и затем вычисляются приведенные затраты. Входным аргументом
целевой функции является вектор значений диаметров труб.
5.1.
Создание матрицы
коэффициентов 
.
Элемент этой матрицы 
равен коэффициенту в
уравнении (1), записанном для связи между узлами с номерами 
и
. (2)
Проводится
симметризация матрицы.
5.2.
Составление уравнений
для давлений.
Для этого находятся положения единиц в i - ой строке матрицы
связей. Их число дает количество выходящих расходов из узла с номером 
, а номер единицы в строке - номер узла, в который идет
поток. Для каждой пары индексов составляется уравнение
. (3)
Полученные уравнения объединяются в массив.
. 5.3.Составление
списка неизвестных давлений.
Давления во всех узлах считаются неизвестными.
Так как число неизвестных на одно больше, чем число уравнений, надо задать
давление в одном из узлов (можно взять любой
узел с известным давлением).
5.4.
Решение системы
уравнений для давлений.
Полученная
система линейных уравнений решается численно методом Гаусса, основная идея
которого состоит в последовательном исключении неизвестных из этой системы.
5.5.
Задание наименьшего
давления.
Определяется положение в списке неизвестных узла
с наименьшим давлением. Ко всем значениям давлений прибавляется такая величина,
которая делает наименьшее давление равным (задано техническими требованиями к
трубопроводу). По этим результатам определяется давление насоса.
5.6.
Определение приведенных
затрат.
По приведенной выше формуле определяется
величина приведенных затрат, которая и является выходным аргументом целевой
функции.
6.
Минимизация целевой
функции.
Минимизация целевой
функции осуществлялась методом Хука - Дживса, несколько измененным в
соответствии со спецификой решаемой задачи.
Покажем эффективность
использования приведенного алгоритма для гидравлической системы, расчетная
схема которой приведена на рис.1. Здесь: 1 – насосная станция, 3,5,7,9,10, и
т.д. – дома квартала, 4, 6, 8, и т.д. точки разветвления трубопроводов системы. Приведенная схема соответствует
схеме водоснабжения одного из типичных городских кварталов.
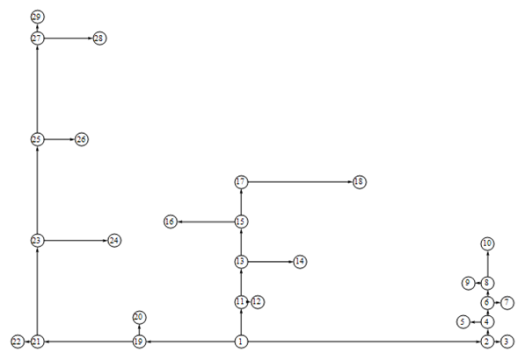
Рис. 1. Расчетная схема
гидравлической системы
Матрица расстояний трубопроводной системы
В результате оптимизации
целевой функции приведенные затраты уменьшилось на 18%.
Выводы
Выполненные авторами
исследования показали, что предложенная методика выбора рациональных параметров
сложной гидравлической системы позволяет значительно уменьшить приведенные
затраты. Причем, ее использование целесообразно как на
стадии проектирования системы, так и при ее модернизации.
Литература
1.
Абрамов
Н.Н. Водоснабжение. Учебник для вузов. Изд. 2-е перераб. и доп / Н.Н. Абрамов.
– М. : Стройиздат, 1974 – 480 с.
2.
Абрамов
Н.Н. Расчет водопроводных сетей. Изд. 4-е перераб. и доп / Н.Н.Абрамов,
М.М.Поспелова, М.А.Сомов и др. – М. : Стройиздат, 1983 - 278 с.
3.
Базара
М., Нелинейное программирование. Теория и алгоритмы: Пер. с англ./ М. Базара,
К.Шетти. - М.: Мир.- 1982 - 583 с.
4.
Банди
Б. Методы оптимизации / Б. Банди. – М.:
Радио и связь.- 1988 – 128 с.
5.
Коваленко
А.А. Гидравлические и аэродинамические машины / А.А. Коваленко. - Луганск:
изд-во ДонГАСА, 2000. – 78 с.
6.
Пилавов М.В. Сложные гидравлические системы:
моделирование, оптимизация / М.В. Пилавов, А.А. Коваленко, Г.С. Калюжный и др.-
Луганск. : изд-во ВНУ им. В. Даля, 2011. – 112 с.
7.
Численные
методы условий оптимизации. Пер. С англ. / Под. ред. Ф.
Гилла
и
У. Мюррея
- М. : Мир.- 1977 - 290 с.
8.
Avriel M., Nonlinear Programming:
Analysis and Methods, Prentice-Hall, Englewood Cliffs, New Jersey, 1976, p.
322.