ВЛИЯНИЕ ШИРИНЫ ВЫРАБОТКИ НА ФОРМИРОВАНИЕ РАЗРУШЕНИЯ ЗОН

Магистр горного дела К.Б. Казыбек

Научный руководитель доцент, д.т.н. Т.К. Исабек

Карагандинский государственный технический университет, г.Караганды, Республика Казахстан

В настоящее время в горной промышленности идет тенденция перехода к комбинированной разработке месторождения. В связи с этим возникает необходимость оценки устойчивого состояния выработок для безопасного ведения горных работ в подземных условиях. Поэтому, необходимо рассчитать ожидаемые нагрузки, которые будут воздействовать на выработанное пространство.

Существуют различные методы для определения нагрузок на крепь горных выработок. Для определения возможных зон разрушения вокруг выработки использовалась метод граничных интегральных уравнений (ГИУ) с поэтапным нагружением горных пород.

Проведения выработки нарушает естественное состояния массива горных пород, что приводит к дополнительному нагружению массива. Это дополнительное нагружение разбивается на ряд этапов. На каждом этапе нагружения находится напряженно-деформированное состояние упругого массива с переменной внутренней границей. На первом этапе этой границей является контур выработки. На втором этапе – контур зоны разрушения, возникающий на первом этапе и т.д. При этом на каждом этапе нагружения на внутреннем контуре напряжения сохраняют значения, достигнутые на предыдущем этапе нагружения. Принимается, что породы, попавшие в зону разрушения в процессе дальнейшего нагружения, не оказывают сопротивления деформации упругой части массива. Таким образом, на каждом этапе нагружения дополнительные упругие смещения на внутренней границе упругой части массива происходят без сопротивления, как для неподкрепленного контура. В то же время накопленные на предыдущих этапах смещения этого контура сохраняются неизменными [1].

На каждом этапе нагружения решается упругая задача методом граничных интегральных элементов, который в данном случае является наиболее эффективным по причине непредсказуемой сложности промежуточных контуров зоны разрушения в процессе нагружения. На всех этапах нагружения осуществляется оценка достигнутого напряженно-деформированного состояния с помощью принятых критериев прочности. Численный вариант не ограничивает количество критериев разрушения, поэтому используются одновременно и сдвиговой (Кулона-Мора) и разрывной (наибольшие деформации растяжения) критерии.

Задачей моделирования является определение координат контура разрушения выработки, на основании информации о напряженно-деформированном состоянии массива. В этом случае рассматривается вертикальное сечение массива с вырезом, геометрия которого определялась типовыми сечениями выработки. Контур выработки представляется многоугольником. Геометрия этого многоугольника задается координатами узлов (вершины многоугольника). Поскольку вся область вне контура выработки представляет собой бесчисленное множество точек и численный анализ напряженного состояния во всех точках невозможен, то в нашем случае ограничимся рассмотрением конечного ряда точек (n), расположенных в строго определенном порядке. Все исследуемые точки располагаются на лучах (m), исходящих из середины участков на фиксированном расстоянии друг от друга на луче. Анализ показал, что достаточная точность решения задачи при приемлемом времени ее решения достигается при числе лучей 30-40 с расстоянием между точками 0,05 м (см.рисунок.1). Ориентация лучей должна представлять расходящуюся систему с равномерным охватом массива [2].

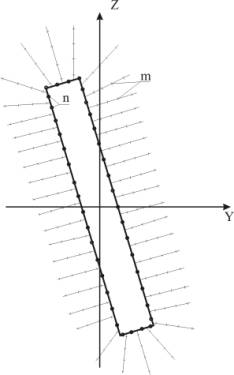
Рисунок 1 – Схема расположения участков на контуре выработки

Для определения устойчивости отрабатываемых блоков №1 и 3 рудных тел №2 и 4 на горизонте + 288м было проведено математическое моделирование для условий рудника Ушкатын-III.

В данной работе моделирования проводилась при следующих параметрах:

- глубина отработки составляет 50 м;

- ширина отрабатываемой жилы 8 и 10 м;

- длина отрабатываемого блока 48 м;

- угол наклона отрабатываемого блока составляет 80⁰;

- прочность (предел прочности на растяжение) вмещающих пород меняется от 1 до 10 МПа.

- коэффициент бокового давления l=1,0;

- коэффициент Пуассона n= 0,25

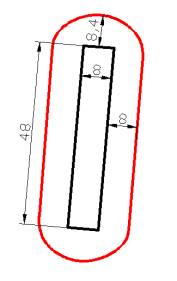
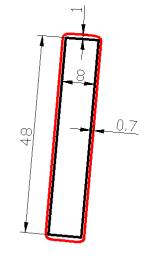
Результаты математического моделирования приведены на рисунках 2 и 3. Моделирование проводилась до 10 МПа предела прочности на растяжение горных пород. Показ рисунков ограничены с 5 МПа, так как свыше 5 зоны разрушения в значительной мере не наблюдается.

В таблице 1 приведены исходные данные для проведения математического моделирование и размеры зоны разрушения при ширине выработки 8 и 10 м.

1 МПа	3 МПа	5 МПа

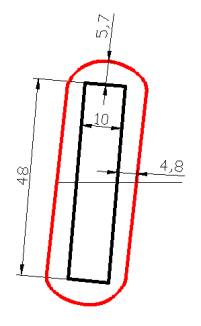
Рисунок 2 – Зоны разрушения вокруг выработки при прочности горных пород на растяжение от 1 до 10 МПа и ширине 8 м

1 МПа	3 МПа	5 МПа

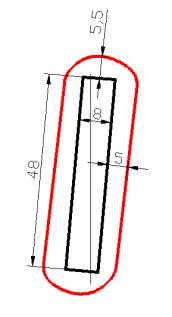
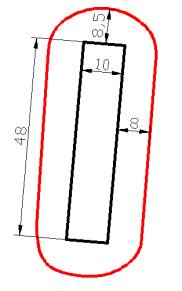
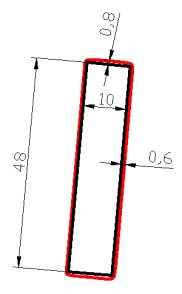
Рисунок 3 – Зоны разрушения вокруг выработки при прочности горных пород на растяжение от 1 до 10 МПа и ширине 10 м

Таблица 1 – Результаты математического моделирования

		Косл	Данные для ввода			Зона разрушения
						при 8 МПа		при 10 МПа
					Ксц	кровля	бока	кровля	бока
100	10	1	2,5	0,65	2,25	-	-	-	-
50	5	1	1,25		1,12	1	0,7	0,8	0,6
100	10	0,2	0,5		0,45	5	5,5	5,7	5
50	5	0,2	0,25		0,22	8,4	8	8,5	8
100	10	0,3	0,75		0,67	4	3,5	3,3	2
50	5	0,3	0,37		0,34	6,5	6,8	6	6,7
100	10	0,5	1,25		1,12	1	0,7	0,8	0,6
50	5	0,5	0,62		0,56	4,5	4,2	4,4	3,8
100	10	0,7	1,75		1,57	-	-	-	-
50	5	0,7	0,87		0,78	3	1,8	2	1
100	10	0,8	2		1,8	-	-	-	-
50	5	0,8	1		0,9	1,7	1	0,8	0,5

Результаты моделирования были обработаны статистическими методами для нахождения аналитических зависимостей развития зоны разрушения от прочности горных пород на растяжение.

Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки статистической информации на ЭВМ, делает практически осуществимым оперативное решение задач изучения корреляционной связи любых показателей методами корреляционно-регрессионного анализа.

Оценка точности аппроксимации парной модели производится по индексу детерминации R.

Проверка практической значимости синтезированных в корреляционно-регрессионном анализе математических моделей осуществляется посредством показателей тесноты связи между признаками х и у.

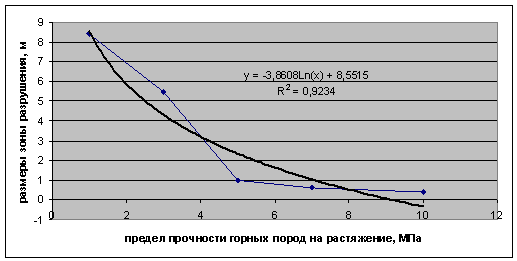
Рисунок 4 – Зависимость размеров зоны разрушения от прочности горных пород на растяжение при ширине выработки 8 м

Показатель R² называется индексом детерминации (причинности). Он выражает долю факторной дисперсии в общей дисперсии, т.е. характеризует, какая часть общей вариации результативного признака у объясняется изучаемым фактором х.

Коэффициент детерминации (R² ) показывает насколько процентов значения У зависят от значения Х. Значение R² находится в пределах от 0 до 1 и чем ближе данное значение к 1.0, тем лучше аналитическая зависимость описывает фактические данные.

В качестве уравнения для описания размеров зоны разрушения вокруг очистной выработки были приняты следующие: линейная, логарифмическая, степенная, экспоненциальная и полиноминальная. В результате проведенных расчетов высокое значение R²=0.9234 при ширине выработки 8 м (см.рисунок 4)и R²=0.9075 при ширине выработки 10 м (см.рисунок 5) получено для логарифмической зависимости.

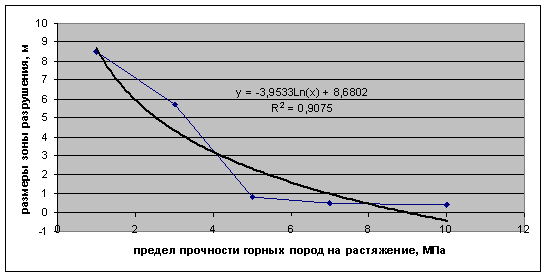
Рисунок 5 – Зависимость размеров зоны разрушения от прочности горных пород на растяжение при ширине выработки 10 м

Как видно из рисунков зона разрушения достаточно равномерно охватывает горную выработку. Причем, как показали исследования, при изменении размеров ширины выработки не оказывают существенного влияния на размеры зона разрушения при прочности горных пород на растяжения от 1 до 10 МПа. Во всех случаях она значительна и определяется больше шириной, чем высотой выработанного пространства.

Литература:

1. Бессонов В.В., Имашев А.Ж., Судариков А.Е., Бахтыбаев Н.Б., Тилеухан Н. Определение устойчивости междужильных целиков методами математического моделирования. Труды Университета, №1, КарГТУ, Караганда. 2010 г.

2. Колоколов С.Б. Расчет параметров поддерживающей и анкерной крепи горизонтальных горных выработок. Учебное пособие/Карагандинский политехнический институт. Караганда, 1990. 64с.