Бакиров Ж.Б., Таженова Г.Д.
Карагандинский государственный
технический университет
Анализ нелинейных систем виброзащиты
численными методами
Создание эффективных средств защиты от
вибрации и ударов является одной из важных проблем современной техники. Особенно
большое значение приобретают эти вопросы для технологических машин и таких транспортных
средств как летательные аппараты, автомобили, морские суда.
Опыт проектирования и эксплуатации
реальных виброзащитных систем показывает ограниченность хорошо разработанной
линейной теории виброзащиты. Возникновение нелинейных эффектов является
следствием увеличения интенсивности вибрационных и ударных воздействий и
нелинейности упруго-диссипативных характеристик виброизоляторов. С другой стороны
применение виброизоляторов с нелинейными характеристиками в ряде случаев может
оказаться полезным. Расчет нелинейных виброзащитных систем обычно проводится
приближенными аналитическими методами [1]. В данной работе приводится методика
их расчета численными методами.
Универсальным методом решения нелинейных
дифференциальных уравнений является применение численного интегрирования. Одним
из эффективных алгоритмов является использование метода Рунге—Кутта четвертого
порядка точности.
Пусть поведение системы описывается нелинейным
уравнением в нормальной форме Коши
![]() (1)
(1)
где ![]() ,
, ![]() - векторы фазовых переменных состояния и внешнего
воздействия;
- векторы фазовых переменных состояния и внешнего
воздействия; ![]() - нелинейная
вектор-функция.
- нелинейная
вектор-функция.
Согласно методу Рунге—Кутта значение вектора ![]() вычисляются по
следующему алгоритму
вычисляются по
следующему алгоритму
![]()
где ![]() ;
; ![]() — шаг
интегрирования по времени;
— шаг
интегрирования по времени;
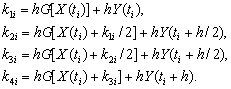
Уравнение (1) интегрируется при следующих
начальных условиях ![]() . Если исследуется установившееся движение, то начальные
условия выбираются произвольно, а участок установления колебаний исключается из
анализа.
. Если исследуется установившееся движение, то начальные
условия выбираются произвольно, а участок установления колебаний исключается из
анализа.
Движение виброизолированного объекта
описывается дифференциальным уравнением второго порядка [2]
![]() (2)
(2)
где m, x - масса и смещение объекта; F(t) - внешнее
воздействие;
![]() - сила, возникающая в
виброизоляторе.
- сила, возникающая в
виброизоляторе.
Это уравнение можно свести к виду (1), если ввести
фазовые переменные ![]()
![]() Тогда векторы в (1)
будут равны
Тогда векторы в (1)
будут равны
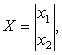
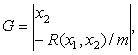
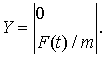
Ввиду практический важности
дифференциальных уравнений второго порядка разработаны схемы численного
интегрирования этих уравнений [3]. Приведем схему Рунге- Кутта четвертого
порядка для уравнения (2):
![]() (3)
(3)
где
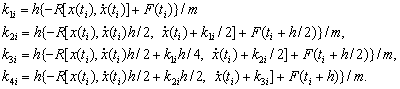 (4)
(4)
После
определения фазовых переменных находим силу в виброизоляторе
![]()
В
ходе расчета определяем максимальное значение этой силы и коэффициент эффективности
виброизоляции
![]()
![]()
Если внешнее воздействие является
случайным процессом, то необходимо отдельное моделирование этого процесса. Чаще
всего реальные процессы имеют дробно- рациональную спектральную плотность:
экспоненциально-коррелированный
процесс ![]()
процесс
со скрытой периодичностью ![]()
косинусоидальный
процесс ![]()
В этих выражениях σ2- дисперсия
процесса; ![]() - параметр широкополосности; θ- несущая частота
узкополосного воздействия.
- параметр широкополосности; θ- несущая частота
узкополосного воздействия.
Их можно рассматривать как результат прохождения
нормального белого шума через линейную систему с постоянными коэффициентами,
называемую формирующим фильтром. Методика вывода уравнения формирующего фильтра
для таких процессов приведена в работе [4]. Для приведенных случайных процессов
уравнения фильтра примут вид соответственно
![]() ,
(5)
,
(5)
![]() ,
,
![]()
![]()
где ![]() - нормальный белый
шум единичной интенсивности.
- нормальный белый
шум единичной интенсивности.
Многие вычислительные комплексы имеют
блоки, генерирующие последовательность нормально распределенных псевдослучайных
чисел единичной интенсивности. Такие программы несложно составить и
пользователю. Для этого можно воспользоваться одним из алгоритмов, описанных в
[5].
Для моделирования случайных процессов их
значения задают в фиксированные моменты времени ![]() . Для этого уравнения фильтра заменяются их дискретными
аналогами — стохастическими разностными уравнениями. Это можно сделать,
например, по методу Рунге- Кутта. Для этого уравнение движения (1) и уравнение
фильтра надо рассматривать совместно. С этой целью создается расширенное
фазовое пространство, включающее кроме фазовых переменных движения и фазовые
переменные фильтра. В дальнейшем производится численное интегрирование по
методу Рунге- Кутта расширенной системы дифференциальных уравнений. При этом
значения белого шума в процессе вычисления коэффициентов
. Для этого уравнения фильтра заменяются их дискретными
аналогами — стохастическими разностными уравнениями. Это можно сделать,
например, по методу Рунге- Кутта. Для этого уравнение движения (1) и уравнение
фильтра надо рассматривать совместно. С этой целью создается расширенное
фазовое пространство, включающее кроме фазовых переменных движения и фазовые
переменные фильтра. В дальнейшем производится численное интегрирование по
методу Рунге- Кутта расширенной системы дифференциальных уравнений. При этом
значения белого шума в процессе вычисления коэффициентов ![]() следует брать равными
значению в момент
следует брать равными
значению в момент ![]() :
:
![]()
Так, если в (2) внешнее воздействие
является экспоненциально- коррелированным процессом вида, то расширенное
фазовое пространство имеет следующие компоненты:
![]()
![]()
![]()
а
векторы в уравнении (1) с учетом (5) примут вид
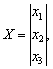
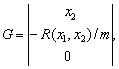

Отметим, что существуют более эффективные
и более точные методы получения стохастических разностных уравнений [6].
Методика вывода этих уравнений приведена в [4]. Там же выведены разностные
уравнения для случайных процессов с вышеприведенными уравнениями фильтра. Так,
для уравнения фильтра (5) получаем следующее разностное уравнение
![]() (5.12)
(5.12)
где ![]() — последовательности
нормально распределенных случайных чисел единичной интенсивности.
— последовательности
нормально распределенных случайных чисел единичной интенсивности.
Значения случайного процесса в дискретные
моменты времени в выражениях (4) согласно (5) определяются так:
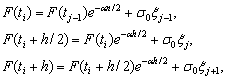
где ![]()
![]()
Для определения вероятностных
характеристик выходных случайных процессов (перемещения, скорости, силы в
виброизоляторе) необходима статистическая обработка их реализации. Для этого
применяется мощный и хорошо разработанный аппарат математической статистики. В
настоящее время имеется множество стандартных программ статистической обработки
случайных процессов, которыми снабжены современные программные комплексы (Matlab, Mathcad и т.д.).
Для оценки эффективности виброизоляции
достаточно определить значения силы в виброизоляторе и путем статистической
обработки определить дисперсию этой силы.
Приведем пример расчета виброзащитной
системы, показанной на рисунке 1. Тело массой ![]() и радиусом инерции
и радиусом инерции ![]() получает ударное
смещение основания в горизонтальном направлении с ускорением в виде
прямоугольного импульса интенсивности а
в течении времени
получает ударное
смещение основания в горизонтальном направлении с ускорением в виде
прямоугольного импульса интенсивности а
в течении времени ![]() . Виброизоляторы имеют резиновые упругие элементы с нелинейными
характеристиками вида
. Виброизоляторы имеют резиновые упругие элементы с нелинейными
характеристиками вида
![]()
где ![]() - перемещение в
виброизоляторе.
- перемещение в
виброизоляторе.
Диссипативные
силы не будем учитывать в виду их малости.
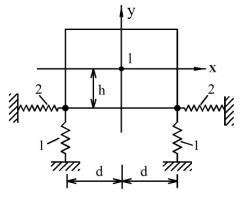
Рисунок 1 – Схема нелинейной виброзащитной системы
Уравнение движения объекта имеет вид
![]()
![]()
где ![]()
![]()
Интегрирование этого уравнения ведем по
соотношениям (3) и (4), трактуя все переменные как двумерные векторы- столбцы:
![]()
![]()
![]()
Численные расчеты приведены при следующих параметрах
системы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При
расчетах начальные условия приняты нулевыми, а шаг интегрирования ![]()
Результаты расчетов в виде графиков изменения
перемещений в виброизоляторах приведены на рисунке 2. Там же приведен график
изменения абсолютного ускорения центра масс объекта, рассчитанный по формуле
![]()
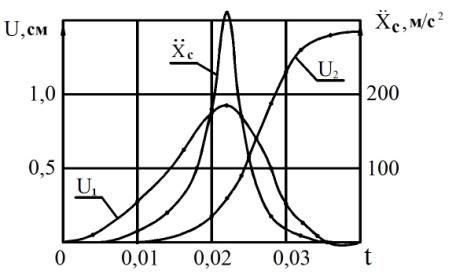
Рисунок 2 – Графики изменения
перемещений в нелинейных
виброизоляторах
Литература:
1. Вольперт Э.Г. Динамика амортизаторов с нелинейными
упругими элементами. –М.: Машиностроение, 1972.-136с.
2. Бакиров Ж.Б., Таженова Г.Д. Расчет нелинейных
виброизоляторов при гармонических воздействиях // Научный вестник НГТУ, №4. -
Новосибирск, 2011. - С. 49 - 59.
3. Корн Г., Корн Т. Справочник по математике. –М.:
Наука, 1973.-831с.
5. Фурунжиев Р.И. Вычислительная техника и ее
применение. –Минск: Выщейшая школа, 1984.-461с.
6. Диментберг М.Ф. Нелинейные стохастические задачи
механических колебаний. –М.: Наука, 1980.-368с.