Современные информационные технологии. 3 Программное обеспечение

Неверова Елена Григорьевна

Университет НАРХОЗ, Республика Казахстан

Применение методов интеллектуального анализа больших данных

Интеллектуальный анализ многочисленных неструктурированных данных становится отдельной областью знаний. Сегодня эта область деятельности требует от аналитиков Big Data компетенций не только в программировании, но и в статистике, лингвистике, математическом моделировании и еще множестве научных сфер.

Как нетрудно заметить, значение материальных (производственных, финансовых, трудовых) ресурсов с точки зрения конкурентоспособности значительно снижается, на первый план выдвигается умение анализировать потоки данных, накапливаемые в информационных системах, а также способность полученных знаний продуцировать новые знания и управляющие воздействия.

Методы интеллектуального анализа данных проходят очередной виток своей эволюции (См. рис.1).

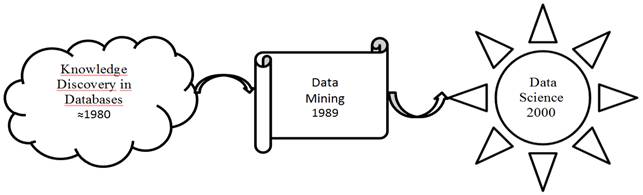
Рисунок 1. Эволюция интеллектуального анализа данных

Если вначале своей истории предпринимались попытки проанализировать большие структурированные данные (Databases), то позднее начался поиск и добыча данных любой природы (Data Mining), а на современном этапе мы имеем дело с наукой о больших данных.

На запрос, содержащий термин «Data Science» поисковая система Google выдает 55 700 000 ссылок.

Можно выделить следующие методы, применяемые при интеллектуальном анализе данных: классификация, кластеризация, ассоциация, прогнозирование и построение деревьев решений.

Дерево поиска оптимальных решений сейчас является едва ли не самым распространенным методом Data Science.

Продемонстрируем построение дерева решений на практическом примере. Имеем массив данных по успеваемости студентов вуза за определенный период. В массив входят разнотипные данные (дисциплины, оценки, посещаемость, наличие публикаций, участие и победы в олимпиадах), часть наблюдений отсутствует (NA).

Требуется предсказать вероятность получения гранта на обучение (Probability_success), исходя из анализа успехов студента в различных направлениях, как то: оценки внутрисеместрового контроля (Grade.VSK1 и Grade.VSK2), участие в олимпиадах (Olimp_partisipate), а также получение призов (Prize_Olimp), участие в научной деятельности (Research_Work) и фактор, понижающий вероятность гранта (Negatives), отражающий пропуски занятий, нарушения регламента вуза.

Для решения задачи был выбран язык программирования R и соответствующая программная среда - R-Studio.

Подключаем массив данных из файла формата csv.

> Session_Result=read.csv("session2.csv", sep=";", header=TRUE)

Структурируем его: удаляем неизвестные значения или, чтобы не исказить структуру массива, подставляем вместо пропущенных значений сгенерированные данные путем преобразования всех значений данной переменной в средние.

Делим массив на обучающую и тестовую выборку, предположим, в пропорции оптимума Парето (80% -Train на 20%=Test) соответственно, исходя из предположения, что закономерности, обнаруженные на обучающей выборке должны так же хорошо объяснить процессы на оставшейся части наблюдений.

> spl = sample.split(Session_Result$ Probability_success, SplitRatio = 0.8)

> Train = subset(Session_Result, spl==TRUE)

> Test = subset(Session_Result, spl==FALSE)

На обучающей выборке строим дерево решений, ищем зависимость искомой переменной (Probability_success) от всех экзогенных переменных.

>S_RTree = rpart(Probability_success ~ Grade.VSK1+ Grade.VSK2 + Olimp_partisipate + Prize_Olimp + Research_Work + Negatives, data = Train, method = "class", minbucket=2)

Выводим полученное дерево в виде графика (См. рис. 2):

>prp(S_RTree)

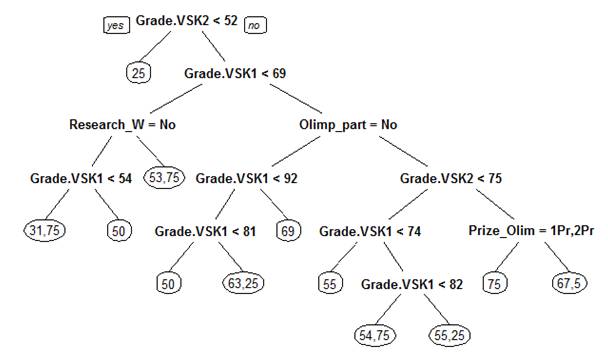
Рисунок 2. Дерево принятия решений по присуждению гранта на дальнейшее обучение *

*Примечание: рисунок построен в R Studio в результате работы на обучающей выборке

В листьях данного дерева находятся искомые вероятности Probability_success.

Из полученного графика можно сделать следующий вывод:

Самая высокая вероятность получения гранта – 75% (правая ветвь дерева) складывается, в первую очередь, из высоких показателей внутрисеместровой успеваемости (Grade.VSK1 и Grade.VSK2), участия в олимпиадах (Olimp_Part) и получения в них призовых мест (Prize_Olim).

Для получения прогноза применяем функцию predict к полученному дереву решений, но строим прогнозную модель уже на тестовой выборке, преобразовав вещественную переменную Probability_success в категориальную Res_Success, где значения переменной лежат в интервале [0,1].

Оцениваем отклонения результатов полученной тренинговой и тестовой модели с помощью матрицы рассеяния.

> library("ROCR", lib.loc="C:/Program Files/R/R-3.3.2/library")

> PredictCART = predict(S_RTree, newdata = Test, type = "class")

> table(Test$Res_Success, PredictCART)

PredictCART

No Yes

No 1 1

Yes 0 10

> (1+10)/(1+1+0+10)

[1] 0.9166667 # точность прогноза

Строим ROC-кривую для определения доли правильно классифицированных положительных и отрицательных исходов (См. рис. 3).

> library(ROCR)

> PredictROC = predict(S_RTree, newdata = Test)

> pred = prediction(PredictROC[,2], Test$Res_Success)

> perf = performance(pred, "tpr", "fpr")

> plot(perf)

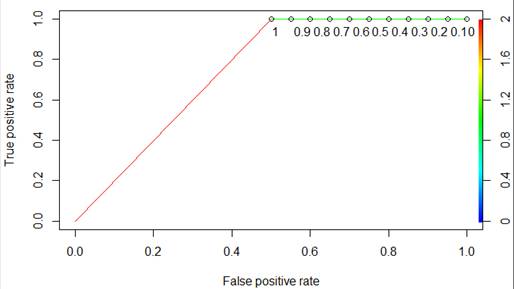
Рисунок 3. ROC-кривая

Вывод: при правильной обработке массива анализ данных на дереве решений дает высокоточный прогноз.

Данный метод достаточно универсален, обладает минимальными требованиями к подготовке исходных данных, дает быстрый и точный ответ на поставленные вопросы, способствует принятию решений в условиях неполной определенности.

Литература:

1. John A. Rice, Mathematical Statistics and Data Analysis. 3rd edition. Duxbury Press India, 2006. - 650 pages

2. An Introduction to R. Notes on R: A Programming Environment for Data Analysis and Graphics. Version 3.3.2 (2016-10-31)

3. С.Э. Мастицкий, В.К. Шитиков. Статистический анализ и визуализация данных с помощью R. Изд.: Хайдельберг – Лондон – Тольятти. 2014. – 401с.