Экономические науки/1. Банки и банковская система

К. ф.-м. н. Жирный Г.Г.

Севастопольский филиал Европейского университета,

кафедра информационных систем и технологий

Определение предельных объемов групп кредитов

с различным уровнем риска

1. Введение. Следует использовать такие методы оценивания принятых банком рисков, которые с заданной высокой степенью надежности обеспечивали бы удержание параметров риска операций банка в наперед заданных границах. Эти методы должны учитывать потенциальное наличие взаимосвязей между способностью различных заемщиков возвращать кредит, например, когда такие взаимосвязи обусловлены общей отраслевой принадлежностью.

2. Формулировка и решение проблемы. В условиях [1] рассмотрим ситуацию, когда концентрация кредитного риска, понимаемая в смысле [2], определяется наличием однородных (в смысле [2]) кредитных договоров, где соответствует группам риска “А”-“Д” ([3]). Оценка ожидаемой доли невозврата равна , которая определяется внутренней методикой коммерческого банка. Пусть истинная доля невозврата составляет , где – ошибка оценивания. Считаем ошибки оценивания независимыми в совокупности для каждого однородного класса. Считаем, что банк не делает систематических ошибок во время оценивания, итак, ошибки имеют нулевое среднее значение: . Далее, банк не делает бесконечно больших ошибок, итак, ошибок имеют конечную дисперсию: .

Допускаем, что в разных классах могут содержаться кредитные договоры, потенциально взаимосвязанные друг с другом. Это предположение существенно расширяет круг возможных приложений нижеследующего результата.

Тогда величина разницы между оцененным кредитным риском и истинным кредитным риском внутри одного класса является однопараметрическим мартингалом [4]. Обозначим его , .

Совокупная величина разницы между оцененным кредитным риском и истинным кредитным риском имеет вид

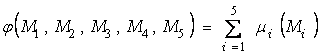
и является многопараметрическим сильным мартингалом [5].

В силу неизвестного характера зависимости между договорами разных классов имеем неизвестный характер зависимости между , . Тогда разумным является использование супремумных (максимальных) неравенств для многопараметрических сильных мартингалов.

Из [5] имеем оценку вероятности отклониться при оценивании доли невозврата от её истинного уровня

,

где параметр есть максимально допустимая ошибка при оценивании доли невозврата от её истинного уровня, сумма отдельного кредита равна , , , ,

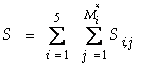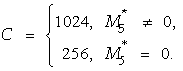
3. Применение. Последнее неравенство дает возможность риск-менеджеру вычислять предельные значення для объемов групп кредитов , таким образом, чтобы вероятность отклониться при оценивании доли невозврата от её истинного уровня не превосходила наперед заданного малого уровня . Для этого необходимо решить относительно , неравенство

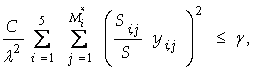
которое в общих предположениях имеет множество решений, так как количество неизвестных параметров равно пяти, а неравенство – одно. Этот факт дает риск-менеджеру возможность выбора при установлении лимитов на различные группы риска. Величины следует оценить, исходя из истории оценивания доли невозврата. Например, в качестве оценки сверху для всех величин можно использовать наблюдаемое стандартное отклонение расхождения между оценкой доли невозврата и её наблюдаемой величиной по всем кредитным контрактам.

Литература:

1. Zhyrnyy G.G. Proactive control of credit risk concentration using martingale random fields. – Abstracts of conference "Functional Methods in Approximation Theory, Operator Theory, Stochastic Analysis and Statistics II", October 01-05, 2004, Kyiv, Ukraine. - Kyiv, 2004. – P.45.

2. Методичні вказівки з інспектування банків “Система оцінки ризиків”. – Постанова N 104 Правління Національного банку України від 15.03.2004р.

3. “Положення про порядок формування та використання резерву для відшкодування можливих втрат за кредитними операціями банків”. – Постанова № 279 Правління Національного банку України від 06.07.2000р.

4. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. – М.: Наука, 1977. – 568 с.

5. Zhirney G.G. Random Fields Theory without Cairoli-Walsh Condition // Proceedings of the Second Scandinavian-Ukrainian Conference in Mathematical
Statistics (Umea, Sweden, 8-13 June 1997), published in Theory of Random Processes. – 1997, v.3(19), N 3-4. – Р.485-490.