УДК 517.43

О ФОРМУЛЕ СЛДЕА АНТИПЕРИОДИЧЕСКОЙ ЗАДАЧИ

ШТУРМА-ЛИУВИЛЛЯ

Шалданбаев А.Ш., Бейсенова Н.Н.,

ЮКГУ им. М.Ауезова, г. Шымкент

Рассмотрим антипериодическую задачу Штурма-Лиувилля:

, , . (1)

Если обозначить через функцию Грина этой задачи, а через - соответствующие собственные числа, то, очевидно, следующие равенства:

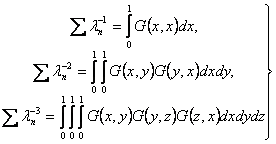(2)

(смысл этих равенств заключается в том, что следы интегрального оператора, обратного к Штурм-Лиувиллевскому, и его итерации выражаются через собственные числа). Давно известен приближенный способ вычисления собственных чисел, основанный на применении равенств (2). (Для конкретных уравнений этот способ восходит еще к Эйлеру, см. также работы Дородницына А.А. [1], Капицы П.Л. [2] и Меймана Н.Н. [3]). Чтобы вычислить с помощью равенств (2) собственные числа, нужно знать функцию Грина уравнения. Если учесть, что начиная с некоторого достаточно большого номера, собственные числа могут считаться известными (равными соответствующим асимптотическим значениям), то для определения первых собственных чисел мы получим алгебраическую систему уравнений. Этот метод бывает иногда весьма удобен, но у него есть и недостаток: он требует значения функции Грина, т.е. оператора, обратному данному дифференциальному. Обратный же оператор выписывается лишь неявным образом, т.е. через решения дифференциального уравнения; поэтому и указанный способ вычисления собственных чисел может быть применен сколько-нибудь эффективно, только если соответствующие решения достаточно хорошо изучены, т.е. лишь для уравнений некоторых простых типов (например, для гипергеометрических уравнений). Для преодоления указанной выше трудности в работе [4] было введено понятие «регуляризованного» следа дифференциального оператора. Эта работа послужила началом целой серий работ, посвященных формулам следов [5]. Работа [6], одного из авторов этой статьи, также была посвящена к этой теме.

Настоящая работа посвящена к первоначальному методу, оказывается для специального класса коэффициентов можно вычислить след обратного оператора к оператору Штурма-Лиувилля с антипериодическим граничным условием. Основная идея работы состоит в том, что мы факторизуем оператора Штурма-Лиувилля, представив его, как произведение двух операторов первого порядка с отклоняющимся аргументом. В результате удается выразить функцию Грина оператора Штурма-Лиувилля непосредственно через коэффициенты уравнения, минуя решении этого уравнения. Результатом наших исследований является следующая теорема.

ТЕОРЕМА. Если - непрерывно дифференцируемая комплекснозначная функция удовлетворяющая условию

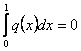, (3)

то след антипериодической задачи Штурма-Лиувилля

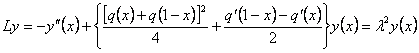, (4)

, (5)

вычисляется по формуле

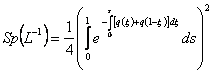. (6)

ЛИТЕРАТУРА

[1]. Дороницын А.А. Асимптотические законы распределения собственных значений для некоторых особых видов дифференциальных уравнений второго порядка. //УМН VII, вып.6 (1952), 3.

[2]. Капица П.Л. Вычисление сумм отрицательных четных степеней корней бесселевых функций. //ДАН 77, №4 *(1951), 561.

[3]. Мейман Н.Н О рекуррентных формулах для степенных сумм нулей бесселевых функций. //ДАН 108 (1956), 190.

[4]. Гельфанд И.М., Левитан Б.М. Об одном простом тождестве для собственных значений дифференциального оператора второго порядка. //ДАН 88, №4 (1953), 593-596.

[5]. Дикий Л.А. Формулы следов для дифференциальных операторов Штурма-Лиувилля. //УМН, т. XIII, вып. 3(81), 1958.

[6]. Шалданбаев А.Ш. Формулы следов для периодической и антипериодической задач Штурма-Лиувилля. //Вестник МГУ, сер. математика-механика, №3, 1982, с.6-11.