2 Механика

С.Р. Гирнис

Павлодарский государственный университет им. С. Торайгырова, Павлодар, Казахстан, e-mail:girnis@mail.ru.

ЗАДАЧА О ДЕЙСТВИИ ПОДВИЖНОЙ НАГРУЗКИ

НА ТОЛСТОСТЕННУЮ ОБОЛОЧКУ В УПРУГОЙ СРЕДЕ

Задачи о действии подвижной осесимметричной нормальной нагрузки на тонкостенную и толстостенную цилиндрическую оболочку в упругой среде рассматривались соответственно в статьях [1,2]. В настоящей работе решена задача о воздействии произвольной подвижной локальной нагрузки на бесконечно длинную круговую толстостенную оболочку, расположенную в упругой среде. Данная задача является модельной при исследовании динамики тоннелей глубокого заложения.

Рассмотрим бесконечно длинную круговую цилиндрическую толстостенную оболочку с радиусом внешней поверхности и радиусом внутренней поверхности в упругом, однородном и изотропном пространстве с параметрами Ламе , и плотностью . Параметры Ламе и плотность материала оболочки обозначим соответственно , ; . В дальнейшем индекс 1 относится к среде, а 2 – к оболочке. По внутренней поверхности оболочки с постоянной скоростью с (меньшей, чем скорости распространения волн сдвига в оболочке и окружающей ее среде) поступательно движется нагрузка P.

Введём цилиндрическую систему координат, ось Z которой совпадает с осью полости. Для среды и оболочки будем пользоваться точными уравнениями теории упругости. Уравнения движения имеют вид

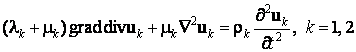, (1)

где , – модули сдвига, – коэффициенты Пуассона – векторы смещений точек пространства и оболочки, – оператор Лапласа.

Так как рассматривается установившийся процесс, то картина деформаций стационарна по отношению к движущейся нагрузке. Если перейти к подвижной системе координат , то уравнения (1) примут вид

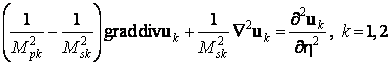, (2)

где – числа Маха; , – скорости распространения волн расширения – сжатия и сдвига в среде и оболочке.

Выражая вектора смещений через потенциалы Ламе

, (3)

преобразуем уравнения (2) к виду

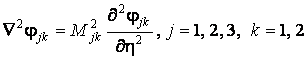. (4)

Здесь .

Используя (3) получаем выражения для компонент напряжённо-деформированного состояния среды и оболочки

,

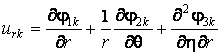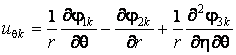, (5)

;

,,

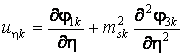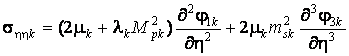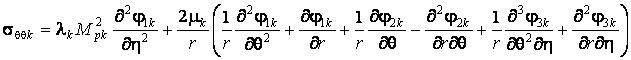
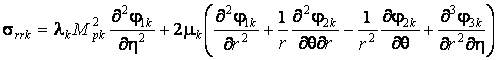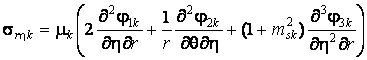, (6)

,

,

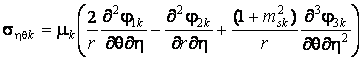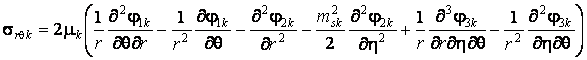где .

Таким образом, для определения компонент напряженно-деформированного состояния оболочки и окружающей её среды необходимо решить уравнения (4) используя следующие граничные условия:

- для скользящего контакта оболочки со средой:

при r = R₁ , , , , , ,

при r = R₂ , ; (7,а)

- для жёсткого контакта оболочки со средой:

при r = R₁ , , при r = R₂ , . (7,б)

Здесь – составляющие интенсивности подвижной нагрузки .

Применив к (4) преобразование Фурье по , находим

, (8)

где , .

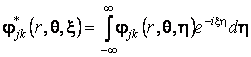Применив к (5), (6) преобразование Фурье по , можно получить выражения для трансформант перемещений и напряжений как функции от .

Так как скорость движения нагрузки меньше, чем скорости распространения волн сдвига в оболочке и среде, то и решения (8) можно представить в виде:

- для среды 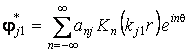, (9,а)

- для оболочки 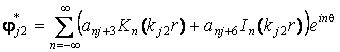. (9,б)

Здесь j = 1,2,3, , ; – функции Бесселя первого и второго рода от мнимого аргумента, – неизвестные коэффициенты, подлежащие определению.

Для определения коэффициентов воспользуемся, в зависимости от условия сопряжения оболочки со средой, переписанными для трансформант граничными условиями (7,а) или (7,б), с учётом (9,а), (9,б) и 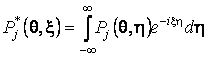. Раскладывая в ряды Фурье по угловой координате, и приравнивая коэффициенты рядов Фурье-Бесселя при , получим бесконечную систему линейных алгебраических уравнений для определения коэффициентов .

Если при любых определитель полученной из граничных условий системы уравнений не обращается в ноль, то после определения коэффициентов , используя обратное преобразование Фурье, можно вычислить компоненты напряженно-деформированного состояния оболочки и среды. Как показывают численные исследования определителя в дозвуковом диапазоне скоростей , обращение последнего в ноль возможно только в том случае, если скорость движения нагрузки не ниже критической скорости [1,2].

Литература:

1. Пожуев В.И. Действие подвижной нагрузки на цилиндрическую оболочку в упругой среде // Строительная механика и расчет сооружений, 1978. – № 1. – С. 44–48.

2. Львовский В.М., Онищенко В.И., Пожуев В.И. Установившиеся колебания цилиндрической оболочки в упругой среде под действием подвижной нагрузки // Сб.: Вопросы прочности пластичности. Днепропетровск, 1974. – С. 98-110.