Технические науки 2

Летучая С.А.

Днепропетровский национальный университет

К ВОПРОСУ О ФОРМЕ КОНТАКТНОЙ ПОВЕРХНОСТИ

Рассмотрим упругое тело , взаимодействующее с абсолютно жестким по площадке предполагаемого контакта . Пусть в результате решения оптимизационной задачи [1] найдено такое распределение контактных усилий , , уравновешивающих внешнюю нагрузку , при котором в напряжение принимает минимальное значение. Назовем оптимальной форму контактной поверхности , обеспечивающую при взаимодействии с распределение усилий _.

Покажем, что оптимальную конфигурацию контактной поверхности абсолютно жесткого тела можно получить, изменив его форму, первоначально совпадающую с контактной поверхностью , на величину , т.е.

, (1)

_,

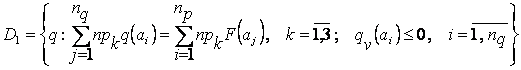где ; – первоначальный зазор между и ; – вектор перемещений узлов предполагаемого контакта от усилий и внешней нагрузки ; – вектор размерности , все компоненты которого равны величине наименьшего перемещения в векторе ; – множество допустимых решений; – проекции на оси координат; – множество узлов конечных элементов; – множество узлов контакта.

Вектор введен в рассмотрение в связи с тем, что решение оптимизационной задачи [2] осуществляется для , нагруженного системой самоуравновешенных сил и . Компоненты вектора могут иметь как положительные, так и отрицательные значения. Однако величина первоначального зазора между и может быть только положительной, причем, хотя бы в одном узле контакта должна быть равна нулю.

Контактная задача для упругого тела и абсолютно жесткого тела с использованием вариационоого подхода и дальнейшей дискретизации минимизируемого функционала по схеме метода конечных элементов сводится к решению системы уравнений

, (2)

с учетом граничных условий , .

Площадка предполагаемого контакта состоит из площадки фактического контакта и площадки , на которой контактная поверхность отстает от контактной поверхности Граничные условия на площадках и имеют вид

, ;

, , .

В том случае, когда , , система уравнений (2) преобразуется следующим образом

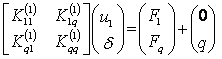, (3)

откуда ; . (4)

Равенство (1) будет доказано, если в результате решения (2) при получим _. Вектор найден в результате оптимизационного поиска, на каждом шаге которого с помощью МКЭ определяется напряженное состояние . Решается система уравнений (2) по найденным значениям вычисляются значения эквивалентных напряжений для всех конечных элементов . На последнем шаге оптимизационного поиска, когда

_,

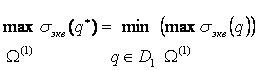система уравнений имеет вид: ,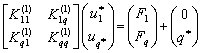

откуда ; . (5)

Решение (2) при перепишется следующим образом

; . (6)

где – перемещение как твердого тела.

При формировании матрицы жесткости конечного элемента для перемещений использовалась аппроксимационная функция [3], составленная таким образом, что узловые перемещения, соответствующие перемещениям элемента как твердого тела, не оказывают влияния на напряженно-деформированное состояние элемента. С учетом этого обстоятельства можно, сравнив выражения (5) и (6), сделать вывод . Равенство (1) доказано.

Приведенное доказательство справедливо также, если , . Однако в этом случае, записав выражения (5) и (6) для -го компонента вектора , можно убедиться, что в выражении (6) , соответствует , в выражении (5).

Литература

1. Летучая С.А. Оптимизация распределения реакций взаимодействия // Вісник Дніпр-го ун-ту. „Ракетно-космічна техніка”, Вип. 2, Д.: РЕВ ДДУ, – 1999. – С. 82-84.

2. Летучая С.А. Метод конечных элементов в контактной задаче // Мат. II МНПК „Наукова думка інформаційного віку’2007”, Т. 3, Д.: Наукова думка, 2007. С. 82-84.

3. Зенкевич О.К. Метод конечных элементов в технике. М.: Мир, – 2007. – 542 с.