УДК 625.1.03,
629.4.015
Абдуллаев Сейдулла
Сейдеметович – д.т.н., доцент (Алматы, КазАТК)
Токмурзина Наталья
Анатольевна – к.т.н., доцент (Алматы, КазАТК)
Пя Дмитрий
Радионович – ассистент (Алматы, КазАТК)
Исследование Методик расчета деформации рельса
под действием подвижного состава
В отделении комплексных испытаний ВНИИЖТа постоянно проводится работа
по созданию и совершенствованию методов расчета взаимодействия пути и
подвижного состава. А.Я. Коганом разработаны статистические методы определения
сил взаимодействия и характеристик напряженного и деформированного состояния
пути. О.П.Ершковым предложен обобщенный аналитический метод определения
поперечных сил в круговых кривых и дана оценка взаимодействия на путь в кривых
различных типов подвижного состава. Л .О. Грачевой разработаны принципиальные
основы статистической теории вынужденных колебаний вагона. В.Д. Дановичем
исследованы пространственные колебания вагонов на инерционном пути. В работах
Ю.С. Ромена проанализированы методы расчетов динамических процессов в подвижном
составе с учетом неровностей железнодорожного пути, рассмотрены вопросы
динамических деформаций рельсошпальной решетки /1-5/.
В настоящей статье изложены результаты разработки метода исследования
динамических процессов и обусловленных ими деформаций рельсовой колеи.
Предлагается математическая модель динамических процессов, протекающих в
подвижном составе и в пути, в виде гибридной системы дифференциальных
уравнений. Разработаны эффективные алгоритмы решения, которые учитывают
нелинейные характеристики связей системы. Разработана общая методика,
математическое и информационное обеспечение расчетов динамических сил и
перемещений железнодорожного экипажа, а также реализован метод определения
мгновенных и остаточных поперечных деформаций рельсошпальной решетки под
воздействием подвижного состава, учитывающий основные нелинейные зависимости в
конструкции пути и действие продольных сил.
При
движении подвижного состава рельс прогибается и передает нагрузку на
подрельсовое основание. Основными параметрами, определяющими величину прогиба рельса, являются осевая
нагрузка, скорость движения, модуль упругости рельсовой стали и параметры подрельсового
основания.
Для повышения точности
расчета на прочность необходимо принимать во внимание как упругие и
диссипативные, так и инерционные
свойства подрельсового основания.
Рассмотрим рельс, лежащий на сплошном упругом основании, несущий
произвольную внешнюю нагрузку P(x).
В
данном случае рельс может быть
рассмотрен как балка на упругом основании. Так называется балка, опирающаяся по
всей своей длине (рисунок 1) на упругое основание, оказывающее в каждой точке
на балку реакцию, пропорциональную у — прогибу балки в этой точке.
Коэффициент пропорциональности обозначается буквой U.
Введение
предположения о пропорциональности реакций прогибу является приближением, хотя
и достаточно близким к действительным условиям.
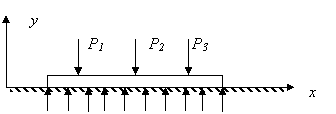
Рисунок 1 – Расчетная схема балки на упругом основании
Предложение
ввести в расчет коэффициент пропорциональности U, именуемый «коэффициентом постели», было впервые
сделано русским академиком Николаем Ивановичем Фуссом в 1801 году. Принимая это
предположение, получаем, что интенсивность реакции основания в каждой
точке сила равна Uy и измеряется в единицах силы и длины; размерность
коэффициента U при этом будет сила и
квадрат длины. Будем считать, что основание оказывает реакцию при прогибах
балки как вниз, так и вверх.
Статически
неопределимой такая балка будет потому, что условие статики— сумма нагрузок
равна всей реакции основания — не дает возможности установить распределение
этой реакции по длине балки, а значит, вычислить изгибающие моменты и
поперечные силы.
Интенсивность
реакции в каждой точке связана с прогибами балки. Поэтому для решения задачи
необходимо найти сначала уравнение изогнутой оси ![]() , а уже
затем формулы для вычисления изгибающего момента и поперечной силы. Ход решения
оказывается обратным обычному.
, а уже
затем формулы для вычисления изгибающего момента и поперечной силы. Ход решения
оказывается обратным обычному.
Найдем
уравнение изогнутой оси для балки постоянного сечения, лежащей на упругом
основании и нагруженной сосредоточенными силами ![]() ...
(рисунок 1). Начало координат возьмем в любой точке, ось х направим
вправо, ось у вертикально вверх. Направление нагрузок вверх будем считать
положительным. Напишем обычное дифференциальное уравнение изгиба
...
(рисунок 1). Начало координат возьмем в любой точке, ось х направим
вправо, ось у вертикально вверх. Направление нагрузок вверх будем считать
положительным. Напишем обычное дифференциальное уравнение изгиба
![]()
Так
как М(х) нам неизвестен, то постараемся связать прогибы непосредственно
с нагрузкой, для этого дифференцируем дважды предыдущее уравнение:
![]() , (1)
, (1)
где q(x)—интенсивность
сплошной нагрузки, действующей на балку в сечении с абсциссой х.
Сплошной
нагрузкой для нашей балки является лишь реакция упругого основания.
Интенсивность ей пропорциональна прогибам; эта нагрузка направлена вверх,
т. е. положительна, когда прогибы идут вниз, т. е. отрицательны,
и наоборот. Таким образом, эта нагрузка имеет знак, обратный знаку прогибов:
![]()
Тогда
![]() (2)
(2)
![]() (3)
(3)
Если
обозначить ![]() , то общий интеграл уравнения (3) имеет вид:
, то общий интеграл уравнения (3) имеет вид:
![]() (4)
(4)
Постоянные
А, В, С, D должны быть определены в каждом частном случае нагрузки и
длины балки. Величина ![]() имеет измерение обратное длине.
имеет измерение обратное длине.
Наиболее просто решается задача об изгибе бесконечно
длинной балки, нагруженной одной сосредоточенной силой (Рисунок 2).
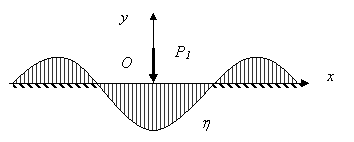
Рисунок 2 –
Расчетная схема балки бесконечной длины.
Начало
координат расположим в точке приложения силы Р. Определим постоянные А,
В, С и D. Так как вся реакция основания, равная силе Р должна быть
конечной величиной, то прогибы балки в точках, бесконечно удаленных ![]() от точки приложения силы, должны обращаться в нуль:
от точки приложения силы, должны обращаться в нуль:
![]() (5)
(5)
При
бесконечно больших значениях х два вторых слагаемых в правой части
формулы (4) обращаются в нуль благодаря множителю![]() , два же первых могут обратиться в нуль лишь при
, два же первых могут обратиться в нуль лишь при ![]() и
и ![]()
таким
образом,
![]() (6)
(6)
Далее,
по симметрии нагрузки и реакции основания, касательная к изогнутой оси в точке
приложения силы должна идти параллельно оси абсцисс:
![]() (7)
(7)
Дифференцируя
(6), получаем:
![]() .
.
Подставляя
в это выражение ![]() и приравнивая
результат нулю, находим:
и приравнивая
результат нулю, находим:
![]() или
или ![]() .
.
Таким
образом, уравнения будут:
![]() (8)
(8)
![]() (9)
(9)
Для
определения последней постоянной С имеем еще одно уравнение: нам
известна величина поперечной силы в начале координат.
Разрезав
балку сечением в точке О справа от силы Р и рассматривая правую
часть балки, видим, что поперечная сита в этом сечении равна реакции основания,
действующей на правую половину балки со знаком минус; так как реакция
направлена вверх (для правой половины) и вся реакция основания равна Р,
значит, поперечная сила в сечении при ![]() равна
равна
![]()
Но, с
другой стороны
![]() (10)
(10)
Таким
образом,
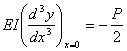 (11)
(11)
Вычисляем,
пользуясь (8), ![]() и
и ![]() :
:
![]() (12)
(12)
![]() (13)
(13)
Подставляя
(13) в (11) и приравнивая х нулю, получаем:
![]() и
и ![]()
Теперь
значения у и ее производных получают
вид
![]()
![]()
![]()
![]()
Таким
образом, напряженное состояние и деформации балки на упругом основании всецело
определяются нагрузкой и коэффициентом ![]() , зависящим от
соотношения жесткостей балки и упругого основания.
, зависящим от
соотношения жесткостей балки и упругого основания.
В работе /6/ исследовано взаимодействия пути одиночной колесной пары (одиночной
вертикальной силы). В реальных условиях железнодорожный путь испытывает
воздействие экипажа (тележки), состоящего из двух и более колес. Поэтому при
исследовании воздействия экипажа на путь необходимо учитывать это условие.
В /5/ приведена методика определения прогибов
рельса под действием группы сил, движущихся с одинаковой скоростью, с помощью
частотных характеристик.
Пусть на железнодорожный
путь действует многоосный экипаж. Общее решение уравнения вида (6) с граничными
условиями (5,7,11) будем искать в виде алгебраической суммы:
![]() , (14)
, (14)
где у1 - прогиб рельса под
первым колесом;
у2 - то же, под вторым колесом;
уk - то же, под k-м
колесом.
Прогиб рельса соответственно под первым, вторым и k-м
колесом, определяется по следующим формулам:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
Тогда общий прогиб рельса
под действием многоосного экипажа будет иметь вид:
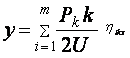 . (18)
. (18)
При движении по пути группы
сил Рi(x,t) (i=1,2, …k), произвольно изменяющихся по
времени и имеющих фиксированные абсциссы
х в подвижной системе
координат, прогиб рельса в любой точке в следствие линейности рассматриваемой задачи, может быть представлен в виде суммы прогибов, вызываемых действием каждой
из n- сил в этой точке.
Уравнение (3) не учитывает динамических параметров
пути: ускорение колеблющихся масс пути; коэффициента неупругого сопротивления
пути и упругого отпора.
Для небольших скоростей
движения подвижного состава нет необходимости
в уравнении колебания рельса учитывать неупругие сопротивления. Однако при высоких скоростях и более тяжелом типе
верхнего строения возникает необходимость
их учета. Силы неупругого
вертикального отпора, развивающиеся
под нагрузкой, могут проявляться
как силы трения, независящие от вертикальных нагрузок, и как силы,
представляющие собой вертикальную
составляющую скоростей колебаний. При этом расчетная схема прогиба рельса под
многоосным экипажем будет иметь вид, представленный на рисунке 3.
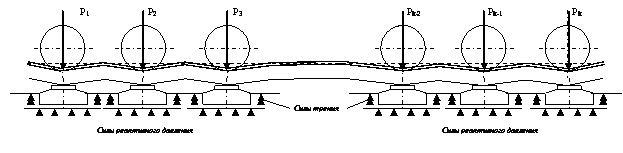
Рисунок 3. Схема воздействия
многоосного экипажа на путь
Также необходимо учитывать силу инерции вращения сечения балки. С учетом
выше названных параметров пути уравнение колебания рельса при воздействии
группы вертикальных сил будет иметь следующий вид:
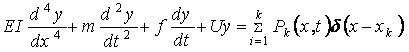 , (19)
, (19)
где EI - изгибная жесткость рельсовой стали;
y -
прогиб рельса;
x - абсцисса текущего сечения рельса,
отсчитываемая от некоторого неподвижного начала координат;
m - приведенная масса;
t - время;
f - коэффициент неупругого сопротивления.
Таким образом, получено
уравнение прогиба рельса в общем виде
для определения суммарного прогиба рельса под действием многоосного экипажа.
Выводы
Напряженное
состояние и деформации балки на упругом основании всецело определяются
нагрузкой и коэффициентом ![]() , зависящим от соотношения
жесткостей балки и упругого основания.
, зависящим от соотношения
жесткостей балки и упругого основания.
Для определения суммарного
прогиба рельса под действием многоосного экипажа получено уравнение прогиба
рельса в общем виде.
ЛИТЕРАТУРА
1. Коган А.Я. Вертикальные
динамические силы, действующие на путь. Труды ВНИИЖТа, вып.
2. Л.О. Грачева. Взаимодействие
вагонов и железнодорожного пути
(вынужденные колебания вагонов). Тр. ВНИИЖ, 1972. Вып.356.207 с.
3. Данович В.Д. Стационарные
колебания бесконечной длины балки, лежащей на упругом основании, под действием
движущейся гармонической нагрузки. Труды
ДИИТа, вып. 199/25.Днепропетровск,1978г.
4. Коган А.Я. Некоторые особенности воздействия на путь
подвижной нагрузки. Вестник ВНИИЖТа,
5. Ю.С. Ромен. Методы
расчетов динамических процессов в подвижном
составе с учетом неровностей
железнодорожного пути в эксплуатации. Диссертация на соискание ученой степени доктора технических наук, Москва,
6. Искакова С.К.
Совершенствование модели расчета железнодорожного пути на прочность.
Диссертации на соискание ученой степени к.т.н. Алматы, 1999г., с.167.
УДК 625.1.03, 629.4.015
Абдуллаев С.С., Токмурзина Н.А., Пя Д.Р. Исследование методик расчета деформации рельса под действием подвижного состава.
Изложены результаты разработки метода исследования динамических процессов и обусловленных ими деформаций рельсовой колеи. Предлагается математическая модель динамических процессов, протекающих в подвижном составе и в пути, в виде гибридной системы дифференциальных уравнений.
Осы
мақалада динамикалық процестерді зертеу әдісін
әзірлеудің нәтижесі және осыған байланысты туатын
рельс табанының деформациялануы келтірілген. Жылжымалы құрам
мен жолдағы болатын динамикалық процестердің
математикалық моделі дифференциальды теңдеудің гибридті
жүйесі түрінде ұсынылады.