Карачун В.В., Мельник В.Н.

Национальный технический университет Украины «КПИ»

ПОСТРОЕНИЕ НЕСТАЦИОНАРНЫХ ФУНКЦИЙ СИСТЕМЫ ДВУХ ЦИЛИНДРОВ В АКУСТИЧЕСКОЙ СРЕДЕ

Рассмотрим систему из двух коаксиальных цилиндров, связаных между собой упругой связью. Наружный цилиндр предполагается упруго податливым, внутрений – абсолютно твердым.

Через щель протяженности на цилиндр воздействует звуковое излучение. Поверхность наружного цилиндра в этом случае приобретает упругие перемещения в направлении паралели и в радиальном направлении , а внутренний цилиндр совершает поступательное перемещение . Здесь угол -центральный угол наружной щели, - координаты точки приложения упругой связи.

Функция . Коэффициенты Фурье (комплексные амплитуды) функции имеют вид:

;

при - определяется формулами

,

,

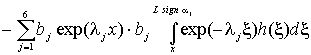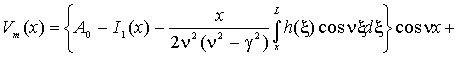
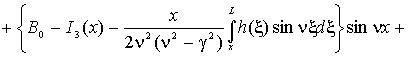
и их аналогами, в зависимости от местонахождения корней характеристического уравнения на комплексной плоскости, которое в свою очередь зависит от находжения корней кубического уравнения на комплексной -плоскости.

Зная коэффициенты Фурье функции , построим ее следующим образом:

. (1)

Некоторые произвольные постоянные в указанных выше формулах остались не вычисленными. Они могут присутствовать и в выражении (1), но быть такими, чтобы ряд сходился. Другие ограничения для этих постоянных будут указаны ниже.

Функция . При коэффициент Фурье этой величины определяется формулой

,

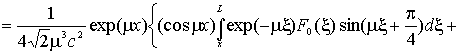
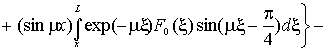
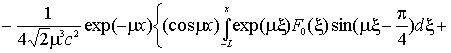
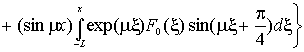При коэффициенты Фурье этой функции находятся из соотношений:

,

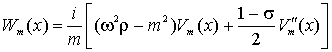где - ранее вычисленные коэффициенты Фурье функции . С учетом этого, функция строится следующим образом –

. (2)

Зависимость (2), подобно выражению (1), содержит произвольные постоянные. Они должны быть такими, чтобы сходились оба ряда – (1) и (2). Но даже и при этих условиях, они определены не единственным образом.

Искомые функции и можно задать однозначно, подчинив каким-нибудь дополнительным условиям, например, потребовав, чтобы они стремились к нулю при .

Функция . Вначале было установлено, что

.

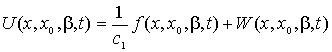и, так как функция, уже найдена, а функция задается формулой (2), то и функция также может быть определена.

В соответствии с выбранной механической моделью, внутренний подвижный цилиндр абсолютно твердый и его поступательное перемещение под действием волны давления определяется функцией , а поверхность наружного – упругая, перемещения которой описываются искомыми функциями и . Точка с координатами лежит в бесконечной полосе (наружная оболочка предполагается бесконечной по протяженности)

.

Функции и зависят от плотности внешней нагрузки , которая при всех значениях и времени сосредоточена в прямоугольнике

полосы и тождественно равна нулю вне этого прямоугольника (рис. 1) . В соответствии с принятой моделью .

Решаемая задача является граничной – отыскиваются все решения, ограниченные в полосе или (второй вариант) - только те, которые обращаются в нуль при .

Если плотность внешней нагрузки и искомые функции и записать в виде рядов Фурье по переменной то по сути дела, задача сведется к определению коэффициентов Фурье и , то есть комплексных амплитуд.

Определяются только те решения, которые ограничены на оси , либо, в частности, обращаются в нуль при .

Для значений получено уравнение шестого порядка относительно , отыскав которое, можно вычислить с помощью первого из уравнений.

Чтобы уравнение при любой допустимой нагрузке имело ограниченное на всей оси решение , необходимо и достаточно, чтобы параметры оболочки, были такими, при которых характеристическое уравнение не имело бы кратных корней на мнимой оси комплексной плоскости или, что то же самое, уравнение не имело кратных отрицательных корней в комплексной -плоскости.

Если же это условие не выполняется и кубическое уравнение имеет двукратный или трехкратный отрицательный корень, то для того, чтобы решение было ограниченным на всей оси, необходимо и достаточно обеспечить функциональную связь функции и нагрузки в виде

,

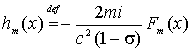, (3)

удовлетворяющем определенным ограничениям. Эти условия не меняются при замене на .

Коэффициенты Фурье и содержат произвольные постоянные. Они должны быть такими, при которых ряды (1) и (2) сходятся. Однако и в этом случае они определяются не однозначно. Чтобы этого избежать, надо также задать начальные условия для перемещений и вдоль образующей цилиндра

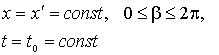(4)

для фиксированного значения . Разумеется, эти условия будут функциями параметра .

Граничные условия задачи могут быть сформулированы и более жестко. Например, вместо того, чтобы требовать ограничения решения в полосе , можно оговорить стремление решения к нулю при вместе со всеми своими производными, при любой допустимой внешней нагрузке. Для этого необходимо и достаточно, чтобы выполнялось условие

,

а характеристическое уравнение не имело бы кратных корней на мнимой оси комплексной плоскости , что равносильно требованию отсутствия в кубическом уравнении отрицательных корней в комплексной -плоскости.

В этом случае ни коэффициенты Фурье и , ни функции и , не будут содержать произвольных постоянных и, следовательно, начальные условия задавать нельзя.

Для таких, более жестких, граничных условий можно применить еще один метод – преобразование Фурье по переменной на оси .