Мельник В.М., Карачун В.В.
Національний технічний
університет України «КПІ»
ПІДВІС ПОПЛАВКОВОГО ГІРОСКОПА З НЕНУЛЬОВОЮ ГАУСОВОЮ
КРИВИЗНОЮ УТВОРЮЮЧОЇ ОБОЛОНКИ
 Розглянемо оболонку
спеціальної форми – опуклу чи угнуту (рис. 1). Позначивши величину підйому параболи С1К
в точці z1=0 за
Розглянемо оболонку
спеціальної форми – опуклу чи угнуту (рис. 1). Позначивши величину підйому параболи С1К
в точці z1=0 за ![]() ,
рівняння лінії меридіану в системі координат
,
рівняння лінії меридіану в системі координат ![]() наведемо у вигляді
наведемо у вигляді
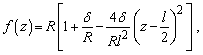 (1)
(1)
де сталі Ламе набувають змісту:
![]()
![]()
Диференціальні
рівняння динаміки оболонки за координатою z мають
наступну структуру –
![]()
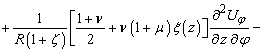
![]()
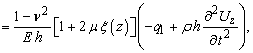 (2)
(2)
вздовж паралелі –
![]()
![]()
![]()
![]()
![]()
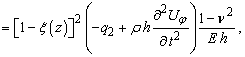 (3)
(3)
в поперечній площині –
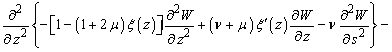
![]()
![]()
![]()
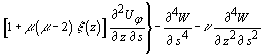
![]()
![]()
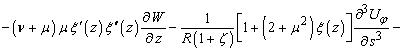
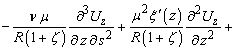
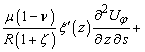
![]()
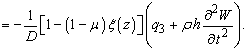 (4)
(4)
Обрана універсальність
математичного опису підвісу
гіроскопа, як оболонки обертання, суттєво розширює можливості аналіза,
дозволяючи оцінювати ступінь впливу багатьох фізико-механічних параметрів
підвісу, а також збурюючих чинників різноманітної фізичної природи та
структури.
Рівняння поплавкового
підвісу зводяться до вигляду, зручного для інтегрування:
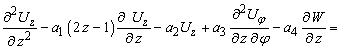
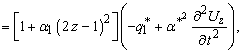 (5)
(5)
![]()
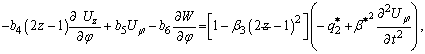 (6)
(6)
![]()
![]()
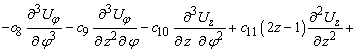
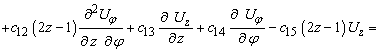
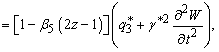 (7)
(7)
де ![]()
![]() - коефіцієнти.
- коефіцієнти.
Як часткове, з цих
рівнянь одержуються рівняння класичного, колового, циліндру. Для цього слід
прийняти: ![]() Отже,
Отже,
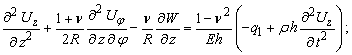 (8)
(8)
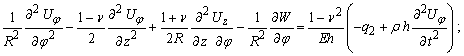 (9)
(9)
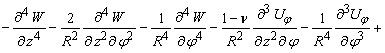
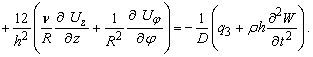 (10)
(10)
Таким чином,
аналітична схема для довільних форм підвісу стала об’єднаною одним структурним
механізмом. Це надає можливість для науково обгрунтованого порівняльного
аналізу.
Залишається провести
процедуру розділу змінних і скористатися методом Бубнова – Гальоркіна.
Зовнішнє збурення
можна навести у вигляді –
![]()
а координатні функції відповідно:
![]()
![]()
![]()
Слід окремо записувати рівняння для значень k=0 (осесиметрична деформація),