Математика/4. Прикладная математика

Каминский Д.Д., к.ф-м.н. Букенов М.М.

Карагандинский Государственный Университет им. академика Е.А.Букетова, Казахстан

ДВУСТОРОННИЕ ОЦЕНКИ В ЗАДАЧЕ О КРУЧЕНИИ ИЗОТРОПНОГО ЦИЛИНДРИЧЕСКОГО БРУСА

Рассмотрим задачу о кручении изотропного цилиндрического бруса:

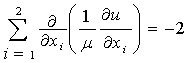, где (1)

,

- константа Ламе. В качестве области D выберем круг единичного радиуса с центром в начале координат. Тогда:

,

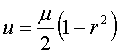Сформулируем вспомогательную задачу метода фиктивных областей для (1):

,

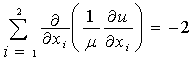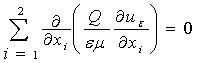, (2)

, ,

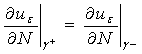
>0 – малый параметр.

В качестве области в задаче (2) выберем круг радиуса два с центром в начале координат.

Полагая Q=1 получим следующее решение (2):

,

,

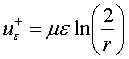В случае Q=-1:

,

,

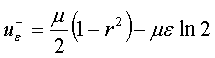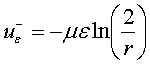Нетрудно проверить что:

,

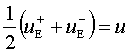, для всех

max ,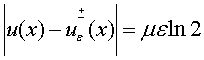

где u – решение (2).

Справедлива

Теорема 1. Существует такое, что для всех верна оценка близости решений задач (1), (2):

(3)

Используя разложение в ряд по степеням

получим следующий результат.

Теорема 2. Для всех справедлива оценка:

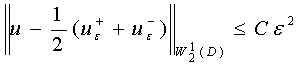
Для того чтобы получить двусторонние оценки решения u(x) с заданной точностью применим идею метода экстраполяции Ричардсона.

Построим экстраполяционные решения , являющихся линейной комбинацией с некоторыми весами

, ,

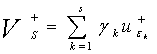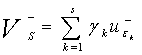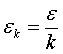, k=1, 2, …, S

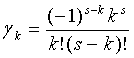, k=1, 2, …, S

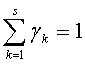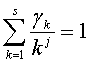, , j=1, 2, …, S-1

Теорема 3. Для всех имеет место