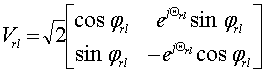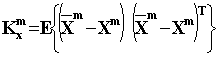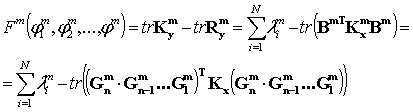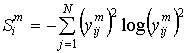УДК 621.391.14:519

К.т.н., проф. Алексеев М.А., Сергеева Ю.В.

Национальный горный университет, Украина

Диагностика технических систем на основе использования параметрически управляемых спектральных операторов

Для обеспечения надежной работы технических систем разного назначения необходимо выполнять функциональный контроль этих систем, который в общем случае включает в себя классификацию текущего технического состояния системы, а также прогнозирование ее состояния.

Целью статьи является разработка метода формирования информативных признаков, характеризирующих конкретное состояние диагностируемой системы. Метод позволяет использовать как достоинства систем базисных вейвлет-функций так и синтезированных ортогональных систем функций, приближенных к характеру анализируемых сигналов и обладающих возможностью параметрического перестраивания.

Во многих случаях решение проблемы функционального контроля и диагностирования объектов связано с распознаванием временных сигналов (вибрационных, акустических и т.д.). Среди широко используемых методов выделения информативных признаков следует выделить основанные на применении ортогональных преобразований, особенно те из них, которые обладают быстрыми вычислительными алгоритмами. Ортогональные преобразования при соответствующем выборе базисной системы обеспечивают адекватность анализируемой информации при высокой степени декорреляции информативных компонент.

В течение последних лет интенсивно развивается принципиально новый класс ортогональных преобразований, основанный на использовании вейвлет-функций. Эти вейвлет-преобразования отличаются высокой степенью локализованности базисных функций как во временной, так и в частотной областях, что позволяет применять их для обработки широкого класса процессов, в том числе и нестационарных. Однако построение новых систем базисных вейвлет-функций представляет собой достаточно сложную проблему.

Основным недостатком Фурье-преобразования является его "глобальная" чувствительность к "локальным" скачкам и пикам функции [1]. Это особенность оказывается полезной для стационарных сигналов, свойства которых в целом мало меняются со временем [2].

При исследовании же нестационарных сигналов требуется использование некоторых локализованных во времени компактных волн, коэффициенты разложения по которым сохраняют информацию о дрейфе параметров аппроксимируемой функции. Попытки построения таких систем функций сводились к сегментированию сигнала на фрагменты ("окна") с применением разложения Фурье для этих фрагментов [2]. Был предложен подход, в котором для различных диапазонов частот использовались временные окна различной длительности. Оконные функции получались в результате растяжения-сжатия и смещения по времени гауссиана. Эти базисные функции называются вейвлетами (wavelets) - компактными волнами [3].

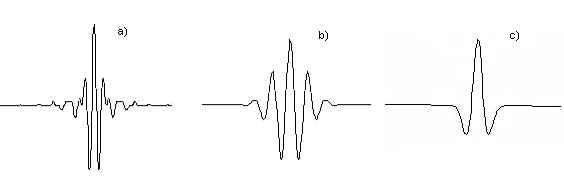
Примеры вейвлетов приведены на рис. 1.

Рис.1. Примеры вейвлетов

a) вейвлет Мейера; b) вейвлет Морле; c) вейвлет ”Мексиканская шляпа”.

Непрерывное вейвлет-преобразование определяется как:

.

Это выражение представляет собой свертку сигнала f(t) с функцией переводящую сигнал из временной в вейвлет-область с базисными функциями:

,

где a и b представляют растяжения и сдвиги одной функции (материнской вейвлет). Параметр a называют параметром масштаба, а параметр b параметром сдвига. Вейвлет-преобразование не уникально в смысле возможности выбора различных материнских вейвлетов. Однако материнский вейвлет должен обладать конечной энергией и ограниченной полосой частот. Коэффициенты дискретного вейвлет-преобразования находятся следующим образом. Сначала выделяют постоянную составляющую сигнала (иногда этот шаг опускается), затем считают свертку сигнала с материнским вейвлетом, растянутым на всю временную ось. После этого материнский вейвлет сжимают в два раза и считают коэффициенты его свертки с первой и второй половинами сигнала. Затем материнский вейвлет сжимают еще в два раза и считают следующие четыре коэффициента. В итоге на первых двух шагах получается по одному коэффициенту, а на последующих шагах число коэффициентов постоянно удваивается. Постоянно сжимающийся материнский вейвлет выявляет все более высокие частоты в спектра сигнала. Его положение на оси времени характеризует момент появления соответствующей частоты.

На рис. 2 изображен вейвлет-спектр вибрационных процессов для различных состояний диагностируемой технической системы. В высокочастотной части спектра выделяются отображения трех дефектных воздействий, обозначенные стрелками.

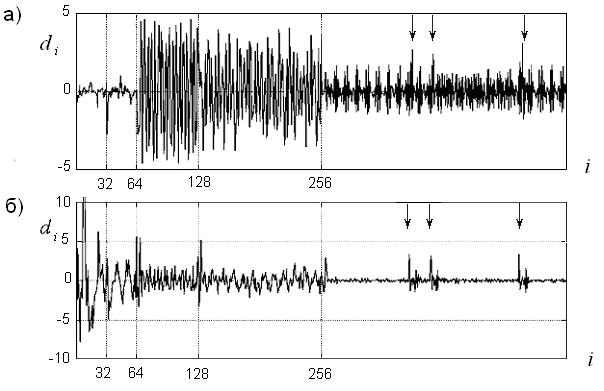
Рис. 2 Вейвлет-спектры вибрационного процесса

Вейвлет-спектры исходных сигналов, как правило, имеют сложный вид для непосредственной интерпретации. Это обстоятельство в значительной степени затрудняет их использование для оценки ситуации на объекте управления. Этот недостаток позволяют устранить базисы, приспособленные к виду исходных данных. В данной статье предлагается использовать вейвлет-спектр в качестве исходного сигнала для дальнейшей обработки с использованием параметрически управляемых субоптимальных по Карунену-Лоэву базисов [4].

В [5] изложен подход к формированию адаптивных матричных спектральных операторов, основанный на их представлении через обобщенное спектральное ядро (), что позволяет получить бесчисленное множество базисных систем функций с алгоритмами быстрых преобразований. При этом матрица спектрального оператора представляется в факторизованном виде: где G_i – разреженные нулями и далее неразложимые матрицы, называемые матрицами Гуда.

В основе матрично-ядерного представления спектрального оператора для р = 2 лежит возможность синтеза базиса из элементарных микроструктур-ядер, обобщенная форма которых имеет вид:

,

где .

Углы параметры и являются степенями свободы ядра и определяют конкретные элементы спектрального оператора.

Охарактеризуем каждый класс вейвлет-спектров соответствующим эталоном и построим базис, приспособленный к эталону [4].

Операция нахождения дискретного спектра цифровыми методами может быть представлена в виде матричного произведения

,

где - вектор анализируемого сигнала размерностью , , - квадратная матрица спектрального оператора размерностью . После формирования базиса , приспособленного к эталону [5], выполним действия для получения из него базиса субоптимального по Карунену-Лоэву.

Для каждого класса векторов получим ковариационную матрицу :

Используем матричный вариант уравнения Фредгольма 2-го рода:

,,

где - матрица спектрального оператора Карунена-Лоэва; - ковариационная матрица в спектральной области оператора Карунена-Лоэва; - матрица, аппроксимирующая в спектральной области адаптивного спектрального оператора.

Поскольку матрица спектрального оператора состоит из собственных векторов матрицы , то , где - собственные значения ковариационной матрицы .

Введем функцию

где - параметры ядер спектрального оператора, не зависящие от вида исходных данных; - слабозаполненные матрицы Гуда, состоящие из ядер с параметрами .

Нахождение субоптимального по Карунену-Лоэву базиса сводится к нахождению минимума функции [4]. При решении задачи построения субоптимальных по Карунену-Лоэву базисов необходимо выбрать алгоритм поиска минимума функции при заданных ограничениях, то есть решить экстремальную задачу.

В [4] определен критерий, по которому случайные векторы относятся к классу m:

если

для всех , то

где . Величину , которая представляет собой квадрат проекции вектора на подпространство размерности , можно рассматривать как меру качества разложения вектора в этом подпространстве. Чем ближе величина к 1, тем лучше качество разложения. В [4] качество разложения предложено оценивать также энтропией распределения энергии по базисным дискретным функциям.

При анализе векторов , , представляющих вейвлет-спектры случайных сигналов, необходимо вначале выполнить нормировку вектора . Далее сформировать систему векторов информативных признаков , процедура формирования которых заключается во вторичном ортогональном преобразовании вектора по субоптимальным по Карунену-Лоэву системам дискретных ортогональных функций :

,

где - квадратная матрица адаптивного спектрального оператора для класса m.

Классификацию вектора можно осуществить по критерию квадрата проекции вектора на подпространство, где 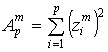, или по критерию минимальной энтропии, где .

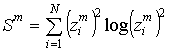Предложенный подход для формирования информативных признаков при сжатии случайных процессов обладает универсальностью, позволяя совместить достоинства вейвлет-преобразования и адаптивных базисов субоптимальных по Карунену-Лоэву, учитывающих особенности класса исходных данных. Следует также отметить, что при предложенном подходе использование базиса Фурье не требует знания априорных данных в виде периода коррелированности случайного процесса. Это не позволяет получить пространство признаков малой размерности на первом этапе их формирования, однако этот недостаток компенсируется применением адаптивных базисов для окончательного формирования признаков. Предложенный подход в достаточной мере удовлетворяет требованиям, предъявляемым к процедуре формирования признаков при сжатии случайных процессов, обеспечивая получения пространства информативных признаков малой размерности, оперативность их формирования (используемые базисы имеют алгоритмы быстрого преобразования), относительно несложную аппаратурную или программную реализацию.

Список литературы

1. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов: Пер. с англ. / Под ред. И.Б.Фоменко. - М.: Связь, 1980. - 248 с.

2. Хэррис Ф.Дж. Использование окон при гармоническом анализе методом дискретного преобразования Фурье // ТИИЭР. -1978. - Т.66. - N 1. - С. 60-96.

3. Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. СПб.: ВУС, 1999, 203 с.

4. Алексеев М.А. Функциональный контроль энергообъектов с применением субоптимальных ортогональных преобразований // Сб.научн.тр. НГА Украины № 4. - Днепропетровск.- 1998, С.67-69

5. Солодовников А.И., Спиваковский А.М. Основы теории и методы спектральной обработки информации: Учебное пособие. – Л.: Изд-во Ленингр. ун-та, 1986. – 272 с.
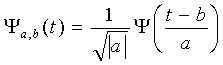