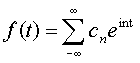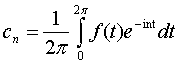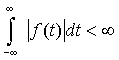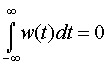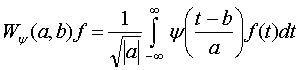Каганская Ю.В.

Национальный горный университет, Украина

Обоснование методики оценки влияния искажений на вейвлет-спектр сигнала

Практически на любом промышленном объекте присутствуют различные физические процессы. Эти процессы являются сигналами, которые несут в себе информацию, необходимую для стабильного функционирования объекта. В сигнале содержатся все данные о том, как протекает тот или иной физический процесс.

Своевременная обработка этих данных позволяет проследить за правильностью выполнения работ на промышленном объекте, либо выявить отклонения от нормы. Поэтому в большинстве случаев результаты необходимо получать в реальном масштабе времени, поскольку какие-либо отклонения сигнализируют о нарушении правильной работы объекта. Если эти моменты не будут обнаружены во время, то могут возникнуть различные неблагоприятные ситуации, начиная от финансовых потерь, до поломки и аварии, что может привести к человеческим жертвам.

Кроме отклонений, связанных с неправильной работой объекта, в производственных условиях всегда имеет место комплекс звуков различной интенсивности и частоты, находящихся в беспорядочном сочетании, которые принято называть шумом. Шумом обычно является некая произвольная функция времени, взаимодействующая (например, путем сложения) с сигналом и искажающая его. Реальные данные, полученные в результате измерения некоторых величин, практически всегда подвержены искажениям - в большей или меньшей степени. Поэтому, необходимо отсеивать шум от полезных составляющих сигнала.

Целью данной работы является исследование влияния различных искажений на вейвлет-спектр сигнала.

В настоящее время произвести анализ сигнала можно различными методами. Самым распространённым видом анализа сигналов является преобразование Фурье временного сигнала в частотную область для получения спектра частот сигнала.

Любая функция f(t) из пространства 2π-переодических квадратично интегрируемых функций может быть представлена в виде ряда Фурье:

,

(1)

Коэффициенты с_n в (1) имеют вид:

,

(2)

Необходимо помнить, что преобразование Фурье можно применить к временной функции тогда и только тогда, когда:

· функция однозначна, содержит конечное число максимумов, минимумов и разрывов;

· функция абсолютно интегрируема, то есть:

,

(3)

Несмотря на свои возможности, преобразование Фурье (ПФ) имеет и некоторые недостатки. Обладая хорошей локализацией по частоте, оно не обладает временным разрешением. ПФ не берет в расчет, что частота колебания может изменяться во времени. Каждый коэффициент ПФ отражает поведение сигнала в целом, т.е. лишь его глобальные свойства. Локальные особенности сигнала (разрывы, скачки, пики и т.п.) дают едва заметные составляющие спектра, по которым обнаружить эти особенности, и тем более их место и характер, практически невозможно [1].

Проанализировав недостатки преобразования Фурье, необходимо отметить, что для выявления искажений в сигналах, этот метод не всегда подходит поскольку дает лишь общее представление о составляющих сигнала, где шум будет распределен на всей полосе спектра частот.

Преодолеть эти трудности можно с помощью вейвлет-преобразования (ВП), которое позволяет определить характер изменения частоты сигнала во времени. ВП имеет существенное преимущество перед ПФ прежде всего за счет свойства локальности у вейвлетов.

Вейвлет-преобразование сигнала состоит в его разложении по базису, посредством масштабирования и сдвигов. Базис – это и есть вейвлет, который представляет собой функцию с определенными свойствами. Под масштабом следует понимать колебательные процессы различной периодичности.

Вейвлет-функция должна удовлетворять ряду необходимых условий:

· Ограниченности во времени: w(t)→0, при t→∞;

· Кусочной непрерывности функции w(t).

· Вейвлет должен быть локализован вблизи нуля аргумента, как во временном, так и в частотном пространстве.

,

(4)

Термин вейвлет-преобразование объединяет два вида преобразований - прямое и обратное, которые, соответственно, переводят исследуемую функцию f(t) в набор вейвлет-коэффициентов W_ψ(a,b)f и обратно.

Прямое вейвлет-преобразование осуществляется по такой формуле:

, ,

(5)

где a и b — параметры, определяющие соответственно масштаб и смещение функции ψ, множитель обеспечивает независимость нормы функций от масштабирующего числа a.

Таким образом, любая функция из L²(R) может быть представлена суперпозицией масштабных преобразований и сдвигов базисного вейвлета с коэффициентами, зависящими от масштаба (частоты) и параметра сдвига (времени) [2].

На рис. 1(с использованием вейвлета Хаара) показано, что при уменьшении масштаба, увеличивается разрешение по частоте и уменьшается разрешение по времени, а с увеличением уменьшается разрешение по частоте и увеличивается по времени. С помощью изменяемой частотно-временной вейвлет-функции, можно проанализировать и низкие, и высокие частоты сигнала. Это свойство ВП дает ему большое преимущество при анализе локальных свойств сигналов.

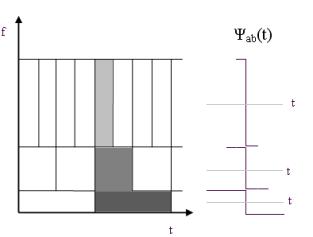
Рис. 1

Таким образом, благодаря изменению масштаба вейвлеты способны выявлять различие в характеристиках на различных частотах, а благодаря сдвигам проанализировать свойства сигнала в разных точках на всем исследуемом интервале.

Поскольку шум является локальной особенностью сигнала, то с помощью вейвлет-спектра можно вычислить его местоположение в сигнале (если искажение произошло только на небольшом участке сигнала), частоты шума и, как результат, избавиться от ненужных помех.

Подавление шума может быть произведено простым путем удаления детализирующих коэффициентов высокочастотных уровней, полученных в результате вейвлет-преобразования. Но вейвлеты имеют и другие возможности. Составляющие шума, и особенно большие случайные выбросы значений сигналов, можно также рассматривать в виде множеств локальных особенностей сигналов. Если задать некоторый порог для их уровня, и срезать по нему детализирующие коэффициенты, то возможно не только уменьшить уровень шумов, но и установить пороговые ограничения на нескольких уровнях разложения с учетом конкретных характеристик шумов и сигналов для различных типов вейвлетов. Это позволяет создавать адаптивные системы очистки сигналов от шумов в зависимости от их особенностей.

Рассмотрим несколько примеров различных сигналов и влияние искажений на вейвлет-спектр.

На рис. 2 проиллюстрированы два одинаковых сигнала, один из которых искажен шумами, а также их вейвлет-спектр. Проанализировав рисунок, можно сказать, что масштабно-временная картина вейвлет-коэффициентов уверенно фиксирует местонахождение вершины сигнала сменой знака коэффициентов, даже в сигнале с помехами. Наиболее темные участки соответствуют локальным максимумам вейвлет-спектра.

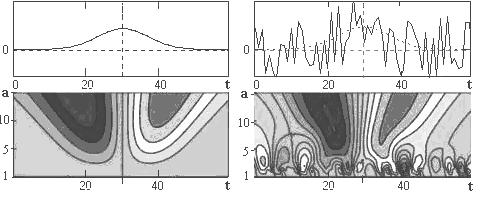
Рис. 2

При изломах функций спектрограммы уверенно фиксируют место изломов максимумами (минимумами) значений коэффициентов, как это показано на рис.3. При наложении на такие функции шумов точное определение места изломов по масштабным сечениям на малых значениях параметра 'а' становится невозможным, однако на больших значениях параметра 'а' такая возможность сохраняется, естественно, с уменьшением точности локализации.

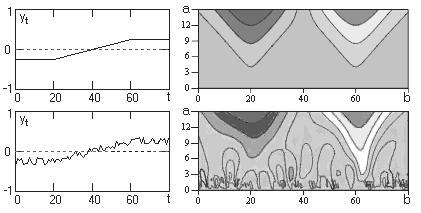
Рис. 3

В результате исследования показано, что вейвлет-спектр позволяет определить не только наличие искажений в сигнале, но и их относительно точное месторасположение. Это возможно благодаря масштабированию и сдвигам самих вейвлет-функций. В отличие от Фурье-преобразования, которое дает возможность определить лишь наличие и значение разных частот спектра сигнала, вейвлет-преобразование показывает положение этих частот во времени.

Следует отметить, однако, что хотя вейвлет-анализ и позволяет достаточно точно определить локальные особенности сигнала, но он не может объяснить их причину. Это уже выясняется в ходе экспериментов, где выводиться зависимость каких-либо особенностей сигнала с отклонениями в работе самих объектов.

Литература:

1. Яковлев А.Н. Введение в вейвлет-преобразования: Учеб. пособие. –Новосибирск: Изд-во НГТУ, 2003. – 104 с.

2. Астафьева Н.М. Вейвлет-анализ: Основы теории и примеры применения. – Успехи физических наук, 1996, т.166, № 11, стр. 1145-1150.

3. Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование – Успехи физических наук, 2001, т.171, №5, стр. 465-481.