Мельник В.Н., Карачун В.В.
Национальный технический университет Украины «КПИ»
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ УПРУГОЙ ПОВЕРХНОСТИ КОЖУХА
ГИРОСКОПА
Дифференциальные
уравнения упругой цилиндрической поверхности кожуха запишем в вид –
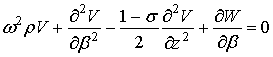 ;
;
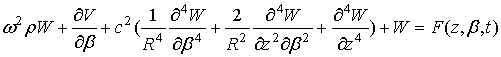 , (1)
, (1)
где ![]() - коэффициент (
- коэффициент (![]() ,
,![]() - толщина и радиус цилиндрической оболочки);
- толщина и радиус цилиндрической оболочки); ![]() и
и ![]() - соответственно тангенциальная и
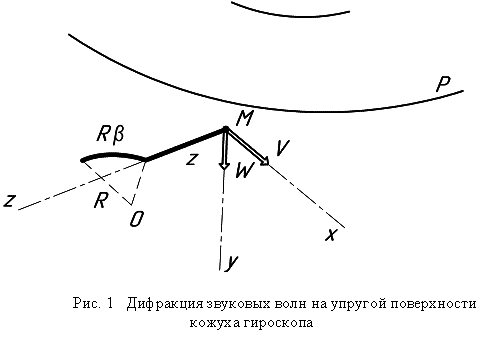
радиальная составляющие перемещения боковой поверхности (рис. 1);
- соответственно тангенциальная и
радиальная составляющие перемещения боковой поверхности (рис. 1); ![]() ;
; ![]() - центральный угол;
- центральный угол; ![]() - длина цилиндра.
- длина цилиндра.
Граничные условия
зададим в виде:
![]() ;
; ![]() ;
; 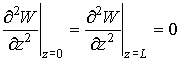 . (2)
. (2)
Пусть в начальный
момент времени ![]() с упругой оболочкой начинает
взаимодействовать волна давления
с упругой оболочкой начинает
взаимодействовать волна давления
![]() , (3)
, (3)
где ![]() - амплитуда плоской
монохроматической волны;
- амплитуда плоской
монохроматической волны; ![]() - координаты точки
- координаты точки ![]() поверхности;
поверхности; ![]() ;
; ![]() ;
; ![]() - косинус угла между нормалью
- косинус угла между нормалью ![]() к фронту плоской волны и
к фронту плоской волны и ![]() -нормалью к поверхности.
-нормалью к поверхности.
Решение
систем уравнений (1) и (2) будем искать в виде рядов Фурье функций ![]() и
и ![]() в прямоугольнике
в прямоугольнике
![]() (4)
(4)
В соответствии с принятыми граничными условиями, ряд Фурье по
переменной ![]() строится в виде –
строится в виде –
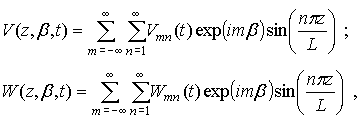 (5)
(5)
здесь ![]() - числа полуволн в плоскости шпангоута и
продольной соответственно.
- числа полуволн в плоскости шпангоута и
продольной соответственно.
Вычислим коэффициенты
Фурье функции ![]() в прямоугольнике (4):
в прямоугольнике (4):
![]() , (6)
, (6)
где
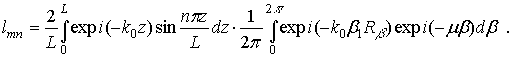 (7)
(7)
Полагая, что ![]() ,
получим –
,
получим –
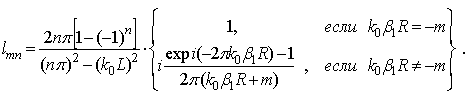 (8)
(8)
Таким образом,
выражение (6) можно преобразовать к виду –
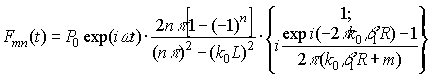 , (9)
, (9)
если ![]() .
.
В окончательном виде
соотношение (8) представляется так –
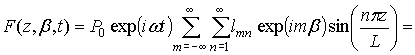
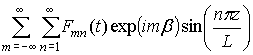 . (10)
. (10)
Если подставить (5) и (10) в исходную систему дифференциальных уравнений (1), то получим:
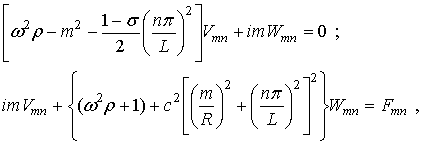 (11)
(11)
где ![]() ;
; ![]() .
.
При ![]() эта система уравнений преобразуется:
эта система уравнений преобразуется:
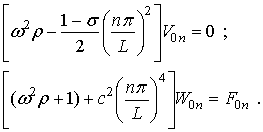 (12)
(12)
Отсюда следует, что
если
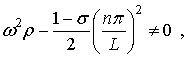 (13)
(13)
то ![]() .
Если же, наоборот,
.
Если же, наоборот,
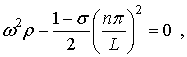 (14)
(14)
то ![]() может принимать произвольные значения.
может принимать произвольные значения.
Вследствие этого, в
качестве исходного, зададим –
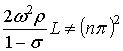
при сформированном выше
ограничении ![]() .
.
Коэффициенты ![]() без особых затруднений найдутся из выражений
(12) –
без особых затруднений найдутся из выражений
(12) –
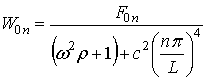 , (15)
, (15)
причем выполнение условия (13)
здесь не обязательно.
Вычислив определитель ![]() системы (11)
системы (11)
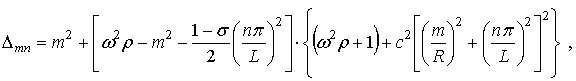 (16)
(16)
при условии, что он не равен нулю
(![]() ),
несложно найти и искомые неизвестные величины:
),
несложно найти и искомые неизвестные величины:
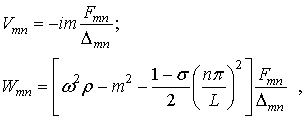 (17)
(17)
где ![]() ;
; ![]() .
.