Т.ғ.к. Абдимомынова
М.М., магистрант Ерманова Г.Б.
М.Х.Дулати
атындағы Тараз мемлекеттік университеті
Криптологиялық
ашық кілтті жүйе әдісінің математикалық моделі
Қазіргі
таңда ақпараттық қауіпсіздікті қамтамасыз ету
жолдары өте көп.Ақпаратты қорғауды
қамтамасыз етуде әр түрлі әдістер мен
құралдар бар. Шифрлау әдістері,ақпаратты
кодтау,әр түрлі кілттерді пайдалану арқылы
ақпараттың қауіпсіздігін қамтамасыз етеміз.
Криптографиялық мәліметті жабу процесі
программалық және ақпараттық түрде жүзеге
асырылады. Ақпаратты іске асыру үлкен бағамен ерекшеленеді,
бірақ тәні мен артықшылығы: жоғары
шығаруында, қарапайымдылығында,
қорғаныштылығында және т.б. Программалық іске
асырылу іскерірек болып келеді. Криптожүйе
симметриялық және ашық кілт (симметриалы емес) болып
бөлінеді. Симметриялық криптожүйеде шифрлеу және
дешифрлеу үшін бір кілт қолданылады. Жүйедегі ашық
кілтте екі кілт қолданылады, олар бір-бірімен математикалық
байланысқан ашық және жабық болады. Барлық
қолданушы адамдар ақпаратты ашық кілттің көмегімен
шифрлей алады, олардың қолында ашық кілт болады, ал тек
хабарламаны алған адам ғана жабық кілттің
көмегімен шифрды аша алады.Кілттерді тарату және басқару
жүйесінде қолданушылар тобы арасында кілттерді жарату және
тарату мәселелері шешіледі.Криптожүйенің
талаптары: Криптографиялық
жабық мәліметтері программалық және
ақпараттық сияқты қолданылуы мүмкін.
Ақпараттықты жүзеге асырудың айырмашылығы
бұл үлкен маңызды құндылық, алайда
оның өзіне тәнділігі және артықшылығы ол:
үлкен өнімділік, қарапайымдылық, қорғаныс
және тағы басқа. Программаны жүзеге асыру өте
қолайлы және қолданылуына рұқсат етеді.Төмендегі
қатынаста маңызды орын алатын, 
- ға негізделген көптеген матрицаларды қарастырамыз:
(1)
Матрицаларда
көбейту ережесін орындай келе, біз келесі мынадай қатынасқа
ие боламыз:
(2)
Теңдік шартын
біз теңдік жүйесі ретінде жазамыз:
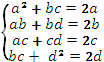
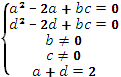
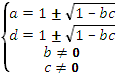(3)
Осылайша, негізінен
түпкі мәні оның квадраттық қалдығы болып
табылатын, яғни кезкелген (b,c)
мәндерінің жұбы үшін, тек қана (a,d) жұбы бар және ол (109)
формулаға сәйкес келетін көбейту жүйесі яғни кері
матрицаны білдіреді. Осы тәріздес матрицаларды дәрежелеу
арқылы біз келесі формуланы шығарамыз немесе есептейміз:
= (4)
Ақырғы
коммутативті емес топтың осындай кері элементтері үшін,
олардың дәрежесін жинақтайтын, әртүрлі элементтер
санының тәртібі тұжырымдамасын енгізуге тиіспіз.
Көбейту ережесіне сәйкес келетін жоғарыда біз
құрған матрицада, егер элементтер қатарында 2 саны
болса онда оны біз (-1)-ге тең деп дәрежелеу арқылы
жаңа матрица құрамыз. Кері элементтер қатарын,
элементтер тізімінің ұзындығы арқылы да
анықтауға болады.
Кері матрицалар
классын былай қорытындылауға болады, яғни көбейту
ережесі арқылы қосалқы класстарды анықтауға
болады.
(5)
- кері матрицада берілген, нөл және бірден өзгеше
қатар элементі. Матрицаларды көбейту ережесіне сәйкес,
төмендегідей нәтижеге ие боламыз.
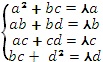
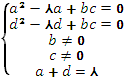(6)
Демек, кез-келген
нөлдік емес (b,c) мәндерінің жұбы үшін, тек
қана мәні оның квадраттық қалдығы болып
табылатын, яғни кезкелген (a,d)
жұбы бар және ол (5) формулаға сәйкес келетін
көбейту жүйесі яғни кері матрицаны білдіреді.
Матрицаның бұл түрі үшін төмендегідей
дәрежелеу ережесін енгіземіз.
= 
(7)
Мұндай кері
элементтер тізімі, қатардың элементі сияқты, 
мәнінің тізіміне
тең келеді. Қайта бекітуді дәлелдейміз.
Бұл
мәндер, мәні тек қана оның квадраттық
қалдығы болып табылатын (b,c) мәндерінің жұбы
үшін кері болып табылады.
Дәлелдеме:
Матрицаны анықтау үшін келесі есептуді жүзеге асырамыз:
Дәлелдеуге не
қажет болды. Енді сол қажеттерді қарастырамыз.
Кері
элементтің бұл типін, әсіресе жасырын қосалқы
топтағы дискретті логарифмін күрделілігіне негізделген ашық кілтті шифрлау крипто
жүйесінде қолдану қызығушылық тудырады.
Ашық кілт төмендегі формула арқылы қалыптасқан:
(8)
Бұл жүйенің
ерекшелігі мынадай, біз жақша ішінде ақырғы коммутативті емес
топтың кері элементіне иеміз, яғни жасырын қосалқы
топтағы дискретті логарифмнің атқаратын жұмысы ол
қайтымсыз мәнге негізделген. Қойылған щартты
қанағаттандыру үшін (7)
кері матрицаны қолдану, криптографиялық жүйенің
қызметін жоғарылатуды жүзеге асырады. Енді біз,
ақырғы топ матрицаларына негізделген ашық кілтті жүйені
қарастырамыз. Бұл жүйе кері элемент арқылы берілген
дискретті логарифмнің жасырын тапсырмасын орындаудан ерекше болып келеді.
(1- сурет)
1. Жөнелтуші
кездейсоқ матрица және кездейсоқ сан U
- ды генерациялайды;
2. Осыдан кейін жөнелтуші
элементтерді есептейді R= 
=
және K=
= U (
=
;
3. K-ны және 
шифрлау кілті түрінде қолдана отырып, жөнелтуші M хабарламасын 
криптограммасына шифрлап тастайды;
4. Жөнелтуші С криптограммасын және R элементін
қабылдаушыға жібереді
5. Қабылдаушы R элементін қолдана отырып, шифрлау кілтін есептейді
=
= X (
=
=
= K;
6. Қабылдаушының келесі қадамы, С криптограммасын сияқты қайта шифрлайды
яғни шифрді ашады. Мұндағы
- шифрді ашу алгоритмнің бір
түрі.
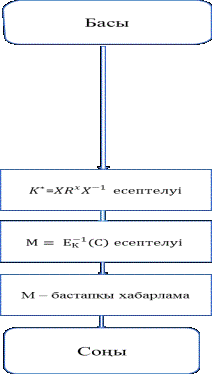
Сурет 1. Кері матрицаға негізделген ашық түрдегі шифрлау
және шифрды ашу
Қолданушының нөлдік жариялаумен сәйкестендіру
әдісі
Бұл әдіс
төмендегі суретте көрсетілген және N кері матрица арқылы берілген дискретті
логарифмнің жасырын тапсырмасын орындау арқылы өңделген.
Мұнда екі байланыспайтын T және N матрицалары осы
әдістің параметрлері болып табылады. Бұл жердегі T, 
қатардағы
үшөлшемді матрица. Қолданушылар өздерінің
ашық кілттерін сенімді орталықта тіркей алады және ашық
кілтті сертификаттарды қабылдайды. Ашық кілттер мына формула
бойынша генрацияланады.
(9)
Формуладағы (x
және w) жеке жасырын кілті болып саналады. N кері матрицасын
қолдану сәйкестендіру әдісінің мықтылығын
дәлелдейді.
Сурет 2. Кері матрицаға негізделген
нөлдік жариялаумен сәйкестендіру әдісі
Сонымен, симметриялық
және симметриялық емес шифрлау алгоритмдерін жұмыс істеуін,
сондай-ақ электрондық цифрлық қолтаңба хабарларды
зерттеу болып табылады. Криптографиялық қайта іске асыру үшін
қорғау және сертификаттау керек.
Қолданылған
әдебиеттер
1.
Хорев П.Б. Методы и
средства защиты информации в компьютерных системах. М.: Академия, 2005. 256 с.
2.
Хоффман Л. Дж.
Современные методы защиты информации / Пер. с англ. — М.: Сов. радио,
1980.-264с.
3.
Грушо А.А., Тимонина
Е.Е. Теоретические основы защиты информации.- Издательство агентства
«Яхтсмен » М.- 1996 -71с.
4.
Мельников В. В. Защита
информации в компьютерных системах Москва «Финансы и статистика»
«Электроинформ» 1997. -368с.
5.
Расторгуев С.П.
Программные методы защиты информации в компьютерах и сетях Издательство агентства «Яхтсмен » М.-, 1991. -368с
6.
Анин Б. Защита компьютерной информации. - СПб.:
БХВ-Санк-Петербург, 2000.-384с.
7.
Милославская Н.Г. Толстой А.И. Интрасети: доступ в Internet, защита: Учебное пособие для вузов. - М.: ЮНИТИ-ДАНА, 2000.-527 с.
8.
Домашев А.В., Попов
В.О., Правиков Д.И., Прокофьев И.В., Щербаков
А.Ю. Программированием алгоритмов защиты информации. Учебное
пособие -М.: «Нолидж», 2000 -288с.