МАТЕМАТИКА / 4.Прикладная математика

Стрюков Р.К.

Воронежский Государственный Университет, Россия

Модифицированный метод ближайших соседей

Введение

В данной статье рассматривается один из возможных подходов к классификации – модифицированный метод ближайших соседей [1,2]. В качестве основных особенностей метода можно выделить:

- использование весовых коэффициентов, которые используются для расчета расстояния;

- использование различных правил принятия решений для отнесения объекта к определенному классу.

Модифицированный метод ближайших соседей

Подробное описание данного метода можно найти в [3], он основан на вычисление расстояния до ближайших соседей. Данное число k является одним из параметров метода и его изменение оказывает влияние на результаты классификации. При отношение некоторого объекта к классу будет приниматься на основе единственного ближайшего соседа (классический метод ближайшего соседа), в результате чего метод теряет обобщающую способность. С другой стороны, если задать параметр k слишком большим, то метод не будет учитывать локальные особенности объекта. Поэтому значение параметра k необходимо задавать в зависимости от решаемой задачи и требуемых результатов классификации [5].

Пусть есть множество объектов, каждый из которых характеризуется определенным набором признаков . Каждый признак оценивается по соответствующей шкале . Пространством признаков называется множество , тогда каждому объекту соответствует векторная оценка .

Пусть имеется разбиение на классы и для некоторого нового объекта определены ближайших соседей, которые имеют с ним наибольшую схожесть. Также рассчитано множество расстояний до каждого из соседей , при этом известно, к какому классу принадлежат соседи-объекты. На основе имеющихся данных необходимо отнести объект к некоторому классу.

Данную задачу можно рассматривать в виде задачи группового выбора на основе голосования [5]: -ым голосом будем считать номер класса, к которому относится -ый ближайший сосед.

Таким образом, ближайшим соседям соответствует выборка длины , каждый элемент которой - номер класса. Введем различные характеристики классов и ближайших соседей объекта .

Пусть из ближайших соседей относятся к классу , - к классу ,…, - к классу , так что . Весом класса назовем величину - относительное количество объектов в классе.

Рангом класса будем называть порядковый номер класса в ранжировании классов по невозрастанию весов (или количеству ближайших соседей объекта ).

Средним расстоянием до класса назовем величину

.

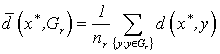Кратчайшим расстоянием до класса назовем минимальное расстояние от до ближайших соседей из класса , т.е.

.

Вкладом объекта в класс называется величина

.

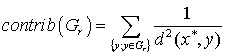Сформулируем несколько типов правил об отнесении объекта к некоторому классу.

1) правило простого большинства [5]: новый объект необходимо отнести к тому классу , объекты которого занимают в выборке более половины мест, т.е. ;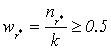

2) правило относительного большинства [5]: новый классифицируемый объект будет отнесен к тому классу, элементов которого окажется больше в выборке из ближайших соседей, т.е. к тому классу, который наберет наибольшее количество голосов

;

3) правило взвешенного большинства заключается в выборе такого класса , номер которого определяется формулой

;

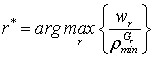4) правило среднего: новый объект относится к тому классу , до которого среднее расстояние минимально, т.е.

5) правило, основанное на критериях качества классификации, состоит в том, что объект относится к тому классу, чтобы вновь полученное разбиение оптимизировало выбранный критерий качества. Например, одним из критериев является компактность классов, поэтому считая, что чем ближе объект класса к объекту , тем больше он вносит вклад в классификацию, можно предложить следующее правило классификации: объект относится к тому классу, для которого его вклад максимальный.

В краткой форме рассмотрим рекомендации по выбору правила классификации:

- если расстояния от до каждого из ближайших соседей приблизительно одинаковы, то можно воспользоваться правилами простого или относительного большинства;

- если ближайшие соседи разбиваются на классы приблизительно одинаковой мощности, то, наоборот, имеет смысл использовать те правила, которые в большей степени учитывают расстояния (например, правило среднего);

- правило взвешенного большинства учитывает и количество объектов в классе (через весовой коэффициент ), и расстояние до этих объектов;

- если классов достаточно много и веса приблизительно равны, то необходимо выполнить выборку таких классов, чтобы их суммарный вес был больше, чем , а затем применить одно из правил.

Учитывая различные критерии качества классификации, можно получить и другие правила.

Заключение

Несмотря на простоту реализации, данный метод показывает хорошие результаты при классификации. Можно выделить следующие преимущества:

- гибкость в выборе правила, на основе которого происходит отнесение объекта к одному из классов, благодаря чему можно оптимизировать алгоритм;

- наличие объясняющей способности и возможности интерпретации результатов классификации;

- довольно простая программная реализация.

Литература:

1. Айвазян С.А. Классификация многомерных наблюдений / С.А. Айвазян, З.И. Бежаева, О.В. Староверов. – М. : Статистика, 1974. – 238 с.

2. Бююль А. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей. – СПб. : ДиаСофтЮП, 2002. – 608 с.

3. Воронцов К.В. Лекции по метрическим алгоритмам классификации [электронный ресурс]. URL:http://www.ccas.ru/frc/papers/voron04mpc.pdf.

4. Base Group Labs, технологии анализа данных [электронный ресурс]. URL:https://basegroup.ru/community/articles/knn

5. Робертс Ф.С. Дискретные математические модели с приложениями к социальным, биологическим и экономическим задачам / Ф.С. Робертс. – М. : Наука, 1986. – 496 с.