Сичікова Я.О.

Бердянський державний педагогічний університет

Математичний опис дифузійних процесів

Процес дифузії звичайно проводиться в два етапи. На першому здійснюють попереднє нанесення домішки. На другому - домагаються проникнення домішки вглиб зразка (перерозподіл концентрацій). Якщо розглядати дифузію як процес переносу атомів у нерівноважній системі, що викликається тільки наявністю градієнту концентрації, то вираз для дифузійного потоку речовини J, тобто кількості речовини, що переноситься в одиницю часу через одиничну площадку перетину (іншими словами швидкості переносу речовини через одиничну площадку), перпендикулярну напрямку переміщення речовини, буде мати вигляд:

J = - D*grad N , (1)

де D* - ефективний коефіцієнт дифузії (см²/с), N - концентрація атомів домішки. Знак «мінус» у рівнянні (1) показує, що дифузія відбувається в напрямку зменшення концентрації домішки.

Оскільки у виробництві ІС ми практично завжди маємо місце з плоскопаралельними структурами, то обмежимося випадком простого одномірного дифузійного процесу, що описується першим законом Фіка (Адольф Фік - німецький фізіолог, який установив закони дифузії в 1855 році), який представляється наступним співвідношенням:

J(x) = - D*[¶N(x,t)/¶x] (2)

Закон (2) описує швидкість дифузії речовини через одиничний переріз деякого середовища при стаціонарному стані дифузійного потоку. Інтенсивність потоку задається величиною D* та градієнтом концентрації.

Другий закон Фіка (рівняння дифузії) визначає накопичення у часі в елементарному об’ємі речовини, що дифундує через одиничний переріз, тобто це різниця між потоком, що входить до об’єму та потоком, що виходить з нього. Це основне рівняння дифузії. Воно відноситься до нестаціонарного стану потоку і характеризується часом від початку динаміки процесу переходу від одного стаціонарного стану до установлення нового стаціонарного стану системи.

Якщо D* = const, то основне рівняння дифузії (другий закон Фіка) можна представити у вигляді

¶N(x,t)/¶t = D*[¶²N(x,t)/¶x²]. (3)

Із формули (3) видно, що другий закон Фіка зв’язує часові та просторові зміни концентрації легуючої домішки.

Розв’язок рівняння проводиться при різних простих початкових граничних умовах.

1. При дифузії домішок у напівнескінченне тіло з обмеженого (скінченного) джерела, коли в тонкому приповерхневому прошарку напівпровідника створена надлишкова концентрація домішки N_o ¹const, розв’язком дифузійного рівняння (другого закону Фіка) є функція Гауса

N(x,t) = N_o*exp(-x²/4Dt). (4)

У цьому випадку N_o залежить від температури і змінюється з часом.

На рис. 1 зображено профіль розподілу легуючої домішки із обмеженого джерела при варіації температури.

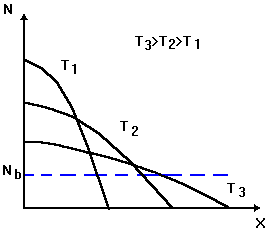
Рис.1. Профіль легування із обмеженого джерела при різних температурах дифузії

2. При дифузії домішок у напівнескінченне тіло з нескінченного (постійного) джерела, коли кількість домішки, що проникає з поверхневого прошарку в об'єм напівпровідника, дорівнює кількості домішки, що надходить ззовні у поверхневий прошарок N_s (N_o = const), розв’язком дифузійного рівняння (другого закона Фіка) є додаткова функція похибок (error function complement) або erfc(x,t) = 1 - erf(x,t), де erf(x,t) - функція похибок (error function) або інтеграл похибок Гауса. Його скорочено позначають erf (z). У відповідності з скороченою назвою цей розподіл називається erf – розподілом

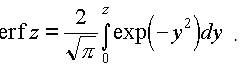
Обидві функції erfc(z) та erf (z) розраховані та табульовані у довідниках.

При цьому вираз для дифузійного профілю домішки має вигляд:

N(x,t) = N_o*erfc[x/2(Dt)^1/2]. (4)

Початкові умови: N(x, 0)=0.
Граничні умови: N(0, t)=N₀, N(x>>0, t)=0.

Залежності нормованих концентрацій від нормованих відстаней для обох розв’язків представлені на рис.2.

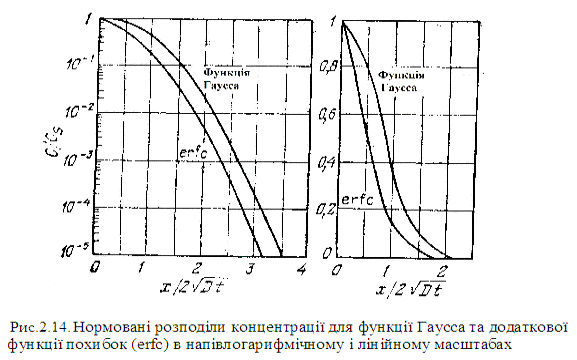
Дифузійні профілі багатьох домішок дійсно добре апроксимуються отриманими виразами (3) та (4). Водночас розподіли багатьох домішок (наприклад, As у кремнії) мають більш складні профілі внаслідок сильної залежності процесу дифузії від концентрації домішки.