Технические науки/12. Автоматизированные системы

управления на производстве

К.т.н. Петров С.В., Зорин А.П.

Украинская инженерно-педагогическая академия, Харьков, Украина

МЕТОДИКА ОПТИМАЛЬНОГО ПЛАНИРОВАНИЯ

ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

Усложнение производственного сегмента и широкое использование современных информационно-вычислительных средств и робототехники выдвигают новые требования к автоматизированным системам управления технологическими процессами (АСУ ТП), разработка и внедрение которых связана с решением ряда сложных проблем. К ним следует отнести: определение степени автоматизации каждого звена системы управления; определение минимально необходимой входной информации и способов ее детализации; выявление необходимой степени обобщения выходной информации для передачи в высшие звенья системы управления; выбор и алгоритмизация решаемых системой задач; разработка схем функциональных и информационных связей в системе, обеспечивающих непрерывность и гибкость процесса управления.

При этом, учитывая тот факт, что в процессе своего функционирования АСУ ТП взаимодействует с АСУ других уровней и назначений суперсистемы, она должна обладать информационной, методической, математической и технической совместимостью.

При проектировании АСУ ТП одной из целей является наиболее эффективное использование ресурсов (материальных, энергетических, информационных) и рациональное распределение функций и объемов решаемых задач между всеми задействованными силами и средствами.

Таким образом, одним из способов повышения эффективности применения АСУ ТП является оптимизация процессов планирования и принятия решений по применению средств в процессе реализации технологического цикла производства (ТЦП).

Поскольку ТЦП представляет собой, по сути, параллельно-последовательный процесс выполнения операций с учетом интервалов ожидания между последовательно реализуемыми операциями, то продолжительность ТЦП является функцией случайных величин времен операций (и ожиданий), а дисперсия времени выполнения ТЦП является функцией от значений дисперсий распределения времени выполнения каждой операции.

В первом приближении, полагая, что согласно центральной предельной теореме закон распределения времени выполнения ТЦП близок к нормальному, выражение для вероятности выполнения ТЦП за заданное время () можно записать в виде:

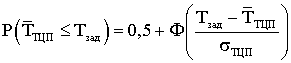, (1)

где - функция Лапласа;

- среднеквадратическое отклонение времени выполнения ТЦП .

На основе (1) можно сформировать критерий наибольшей вероятностной гарантии результата [1]:

, (2)

где G – множество допустимых планов ТЦП.

Использование данного критерия требует осуществлять оптимизацию как по , так и по . Однако, влияние на вероятность значительно меньше, чем .

Поэтому, в рассматриваемых условиях, максимум в выражении (1) будет достигаться при минимальном значении . В связи с этим, вместо критерия (2) для оптимизации ТЦП можно использовать, так называемый критерий наибольшего среднего результата [1]. Данный критерий рекомендует выбирать в качестве оптимальной стратегию управления J, для которой

. (3)

Таким образом, в общем виде задачу оптимального планирования операций ТЦП можно сформулировать следующим образом: необходимо спланировать работу имеющихся средств так, чтобы обеспечивалось выполнение всех поставленных задач в заданное время с требуемой вероятностью или, иными словами, необходимо составить план проведения операций ТЦП, реализация которого обеспечивала бы максимум критерию оптимизации при заданных ограничениях.

Приведем постановку рассматриваемой задачи. Исходными данными будут являться ограничения, накладываемые на процесс управления ТП. Основополагающими являются следующие ограничения.

Во-первых, это ограничения задающие отношения совместимости в момент времени t и предшествования на множестве операций (техническая совместимость операций; энергетическая совместимость операций, которая определяется путем сравнения требуемого для одновременного проведения запланированных операций уровня потребляемой энергии с допустимым; логическая совместимость операций; отношение предшествования операций).

Во-вторых, это ограничения, связанные с особенностями и правилами выдачи управляющей и программной информации.

И в-третьих, это ограничения задающие приоритетность одних операций перед другими (как правило, данное ограничение задается в виде набора правил предпочтения).

С учетом вышесказанного сформулируем задачу оптимизации ТЦП следующим образом.

Найти матрицу моментов начала операций, входящих в состав ТЦП, удовлетворяющую заданным ограничениям и доставляющую основному показателю (3) абсолютный максимум по сравнению со всеми другими матрицами моментов начала операций, отвечающими тем же условиям и ограничениям.

Для выполнения требований, предъявляемым к управлению ТП, необходимо для каждой операции определить интервалы времени, в пределах которых возможно выполнение данной операции, чтобы выполнялись заданные условия и ограничения на всем интервале планирования.

Для эффективного моделирования процесса выполнения ТЦП наиболее удобным является аппарат сетей Петри (СП) [2, 3].

Согласно основам теории сетевого планирования и управления [3, 4], прежде чем приступать к составлению сети (сетевого графа), необходимо: установить, какие операции должны быть завершены раньше, чем начнется данная операция (какие операции должны предшествовать данной операции); определить, какие операции могут быть начаты после завершения данной операции; выяснить, какие операции могут выполняться одновременно с данной операцией.

При наличии таких исходных данных топология сети определяется однозначно.

Учитывая особенности процесса управления ТП, можно предположить, что существует целое семейство СП, отражающих все возможные комбинации взаимозависимостей операций. Естественно, что это семейство должно быть допустимым с точки зрения заданных потребностей, условий проведения и ограничений.

Взаимозависимости между операциями можно задавать специальными матрицами, содержащими информацию о том, какие операции могут выполняться параллельно с данной операцией, какие операции должны быть обязательно завершены раньше, чем начнется данная операция, в каком интервале времени должна быть осуществлена повторная реализация данной операции. В связи с этим, нельзя однозначно построить СП. Перебирая различные допустимые комбинации технологических связей между операциями, определяется некоторое множество допустимых сетей .

Так как, после окончания i-й операции до начала j-й должно пройти некоторое время (время ожидания), то учитывать это время можно путем отображения его в виде фиктивной операции (), имеющей один вход от условия и один выход к событию . () - исходные события и позиция, которые не имеют предшествующих позиций. () - завершающие событие и позиция, которые не имеют ни одного события-последователя. Условие срабатывания переходов (кроме ): наличие фишек во входных позициях. Каждой фишке поставим в соответствие некоторое действительное неотрицательное число - вес фишки . Переходам , отображающим выполнение истинной операции, ставится в соответствие время выполнения i-й операции , а переходам, которые отображают фиктивные операции - соответствующее время ожидания (остальным переходам - 0). Назовем эти числа временными задержками перехода.

Таким образом, задача состоит в том, чтобы из обобщенной сети с контурами выделить множество бесконтурных сетей, структура которых соответствовала бы заданным ограничениям и условиям совместимости операций, а затем из выделенного множества найти оптимальные по критерию минимального времени выполнения.

Перед тем, как приступить к решению этой задачи, коротко рассмотрим процесс моделирования выполнения операций ТЦП с помощью некоторой выделенной детерминированной СП. В момент начала в начальную позицию помещается фишка весом . Переход срабатывает при наличии фишек во всех входных позициях. При этом в единственную выходную позицию перехода помещается фишка, вес которой равен сумме максимального веса фишки из множества фишек, находящихся во входных позициях перехода, и времени задержки сработавшего перехода. В отличие от классических СП, после срабатывания перехода фишки из входных позиций не изымаются, а переход закрывается (т.е. каждый переход может сработать только один раз). Процесс моделирования заканчивается при наличии фишек во всех позициях. При этом вес фишки в позиции соответствует наиболее раннему сроку завершения i-й операции; вес фишки в завершающей позиции равен времени выполнения ТЦП для рассматриваемой сетевой модели.

Разобьем множество T переходов сети на "ярусы", а также определим множество со-сечений и li-сечений обобщенной сети [2, 3].

Пусть базовым сочетанием операций (переходов) называется допустимая, неповторяющаяся комбинация операций, которую можно реализовать в одном ярусе.

Оптимальную сетевую модель плана выполнения ТЦП можно выделить из обобщенной сети. Для этого достаточно из обобщенной сети выделить множество бесконтурных сетей. Каждая такая сеть однозначно определяет план выполнения ТЦП и наоборот.

Для организации целенаправленного перебора сетей множества , т.е. реализации идеи метода ветвей и границ, можно использовать процедуру последовательного разбиения множества на подмножества.

Рассмотрим множество М всех возможных последовательностей операций . При этом будем учитывать, что если какая либо i-я операция в рассматриваемой последовательности расположена ранее, чем j-я, то номер яруса, в котором находится i-я операция, не может превышать номера яруса, в котором находится j-я операция. Очевидно, что каждой последовательности соответствует свое значение времени Т выполнения этой последовательности операций при реализации ТЦП. Согласно сформулированной выше задаче оптимизации плана ТЦП по критерию быстродействия, необходимо найти оптимальную последовательность операций, то есть ту, для которой , а следовательно, и соответствующую ей бесконтурную сеть . Для решения этой задачи методом ветвей и границ необходима разработка соответствующих процедур ветвления, оценки и отсечения.

1. Ветвление. На первом шаге разбиваем множество М на непересекающиеся подмножества , где - множество тех последовательностей операций, которые могут начинаться операцией i. На втором шаге каждое множество разбивается на непересекающиеся подмножества , где - множество тех последовательностей операций, которые могут начаться парой операций . Аналогично разбиение множеств на последующих шагах. После -го шага получим разбиение множества М на подмножеств вида , включающих каждое одну последовательность операций .

Процесс ветвления удобно представить в виде "растущего" выходящего дерева , где - множество вершин, обозначающих подмножества, - множество дуг – разбиений данного подмножества.

Описанное дерево имеет число конечных вершин, равное числу различных последовательностей операций, и называется деревом полного перебора. При отсутствии каких-либо ограничений на порядок следования операций . Наличие одного ограничения на порядок выполнения пары операций уменьшает количество конечных вершин дерева как минимум в два раза.

На каждом шаге ветвления мы получаем несколько подмножеств последовательностей операций, сводя тем самым поиск оптимальной последовательности в исходном множестве последовательностей к эквивалентному поиску в нескольких меньших подмножествах. Но искомая оптимальная последовательность может заведомо отсутствовать в некоторых из этих подмножеств. Установив это, можно не продолжать ветвление из вершин, соответствующих указанным подмножествам, т. е. отсечь от дерева перебора ветви, начинающиеся в таких вершинах. Благодаря этому, перебор в процессе поиска оптимальной последовательности операций существенно уменьшается.

2. Оценка. Отсечение бесперспективных ветвей дерева производится с помощью их количественного оценивания. Количественная характеристика последовательности операций определена однозначно лишь на конечных вершинах дерева полного перебора, или, что то же самое, на маршрутах, соединяющих корень дерева с его конечными вершинами. Это связано с тем, что только конечные вершины дерева означают конкретно определенные последовательности операций. Промежуточные вершины означают целые множества последовательностей работ. Поэтому для них возможна лишь оценка времени выполнения последовательности операций, общая для всех последовательностей данной вершины (данного множества).

В соответствии с изложенным, необходимо ввести функцию , заданную на вершинах дерева полного перебора и равную в его конечных вершинах соответствующим значениям , а в остальных вершинах дающая нижнюю границу значения для всех последовательностей операций, входящих во множество .

В качестве верхней границы для всего дерева полного перебора на начальном этапе решения целесообразно использовать значение , определенное приближенным алгоритмом. Назовем это значение опорным и обозначим .

Обозначим: - ранний срок начала i-й операции (т.е. момент времени, раньше которого она не может начаться);

, где - время начала выполнения ТЦП (для простоты будем полагать ), где - длительность i-й операции;

, где - время начала i-й операции, - время окончания i-й операции ().

При отыскании оценок снизу будем опираться на следующие очевидные факты. Пусть имеется некоторый план выполнения ТЦП за время . Тогда, во-первых, время выполнения ТЦП не может быть меньше, чем максимальная сумма раннего срока начала операции и времени самой операции, во-вторых, время выполнения ТЦП не может быть меньше, чем максимальное время последовательности операций по каждому li-сечению сети.

Тогда выражение для нижней оценки оптимального времени выполнения ТЦП примет вид:

, (4)

где - количество li-сечений;

- количество возможных последовательностей операций в j-ом li-сечении;

- время выполнения цепочки операций, определяемой -ой последовательностью в j-ом li-сечении.

Обозначим - минимальное возможное время выполнения совокупности операций, задаваемой j-м li-сечением.

Тогда, в самом простом случае, можно получить выражение для нижней оценки времени

. (5)

где - множество операций, содержащихся в j-м li-сечении;

- время, которое должно пройти между моментом окончания i-й операции и началом k-й.

Рассмотрим некоторую вершину дерева . Эта вершина соответствует некоторой сети , в которой для операций с номерами определен порядок их следования, а для оставшихся операций порядок их следования еще не определен. Обозначим K - фиксированное множество операций , L - оставшееся множество из l операций:

.

Множеству K однозначно соответствует некоторая сеть , отображающая порядок выполнения операций за время . Кроме того, в рассматриваемой вершине дерева можно выделить множество li-сечений сети . Каждое из li-сечений можно представить в виде последовательности операций , где r - количество операций в рассматриваемом li-сечении . Причем операции принадлежат множеству K, а операции - множеству L. Для рассматриваемого li-сечения можно определить нижнюю оценку времени выполнения цепочки операций, определяемой этим li-сечением:

,

где - время выполнения фиксированной последовательности операций ;

- нижняя оценка времени выполнения оставшейся (нефиксированной) последовательности операций рассматриваемого li-сечения, определяемая с помощью выражения (5).

Таким образом, получаем выражение для нижней оценки рассматриваемой вершины:

. (6)

3. Отсечение. Для того, чтобы отсечь от дерева полного перебора ветвь, начинающуюся в вершине необходимо вычислить для этой вершины оценку и сравнить ее с опорным значением . Если , то дальнейшее рассмотрение множества последовательностей операций не позволит выделить последовательность со временем выполнения меньшим, чем время . В этом случае множество как бесперспективное для отыскания оптимальной последовательности исключается из дальнейшего разбиения, то есть ветвь, начинающаяся в вершине дерева, отсекается.

Итак, процесс поиска оптимального плана проведения ТЦП с использованием метода ветвей и границ может быть представлен в виде следующей последовательности действий.

Этап 1. С помощью приближенного алгоритма определяется начальное опорное решение и соответствующее ему время . По формуле (4) определяется общая нижняя оценка . В случае выполнения равенства поиск оптимального плана прекращается, а решением является полученное опорное решение .

Этап 2. Разбиваем множество М всех разрешенных последовательностей операций на подмножества , что означает ветвление корня дерева в вершины первого уровня. Для каждой вершины согласно выражению (6) вычисляем оценку . Сравниваем вычисленные оценки вершин первого уровня с найденным опорным значением . Если для всех , кроме выбранной на первом этапе, , то процедура окончена: и оптимум достигается при последовательности операций, полученной на первом этапе. В противном случае для всех вершин с выбирается не подвергавшаяся ветвлению вершина с минимальным значением . Из этой вершины производится ветвление в вершины второго уровня. Далее из выбранной вершины с минимальной оценкой производится ветвление в вершины третьего уровня и т.д. В результате приходим в новую конечную вершину дерева , в которой . Причем из логики процедуры видно, что . Значение принимается за новое опорное значение. Если , то дальнейшее решение прекращается: при последовательности операций . В противном случае предполагается повторение второго этапа с опорным значением и получением в результате опорного значения , сравнение его с и т.д.

На определенном шаге все вершины первого уровня окажутся рассмотренными, часть отсечена, а другая часть продолжена путем ветвления до конечных вершин , ,…, с соответствующими временами , ,…, где . Таким образом, дерево полного перебора построено (упорядоченный перебор произведен). Решением задачи является вершина с минимальным значением времени , то есть искомому оптимальному плану ТЦП соответствует последовательность операций , для которой время выполнения .

Таким образом, разработанный алгоритм позволяет проводить целенаправленный упорядоченный перебор возможных вариантов построения плана проведения ТЦП.

Проведенный модельный эксперимент показал, что применение алгоритма оптимального планирования на основе метода ветвей и границ дает значительный временной выигрыш по сравнению с полным перебором при количестве операций , и эффективность его применения растет с увеличением числа оптимизируемых операций. В случае необходимости получения всех оптимальных решений разработанный алгоритм при значительном увеличении временных затрат (приблизительно в 1,5…60 раз) все равно обладает существенным выигрышем по времени работы в сравнении с полным перебором.

Таким образом, за счет оптимального планирования последовательности реализации операций ТЦП можно увеличить функциональную эффективность АСУ ТП. Особенности алгоритма позволяют оперативно строить оптимальный план проведения ТЦП с учетом любых ограничений на выполнимость операций на интервале планирования. При этом особенности управления различными типами ТП, могут быть учтены лишь простой заменой матриц, определяющих совместимость и взаимозависимость операций в ТЦП.

Необходимо также отметить, что разработанный алгоритм позволяет определять все возможные планы проведения ТЦП. Это позволит дополнительно к основному плану иметь несколько резервных.

Использование разработанного алгоритма для оптимизации процесса управления ТП позволяет: повысить оперативность принятия решения и увеличить надежность управления ТП; увеличить уровень автоматизации в процессе принятия решений по задействованию средств производства; повысить вероятность выполнения ТЦП за заданное время.

ЛИТЕРАТУРА

1. Куренков В.И. Методы исследования эффективности ракетно-космических систем. Методические вопросы: Учебное пособие. – Самара: Самарский государственный аэрокосмический университет, 2012. – 201 с.

2. Котов В.Е. Сети Петри. – М.: Наука, 1984. – 160 с.

3. Мараховский  В. Б.,  Розенблюм  Л. Я.,  Яковлев  А. В. Моделирование параллельных процессов. Сети Петри. Курс для системных архитекторов, программистов, системных аналитиков, проектировщиков сложных систем управления. – Санкт-Петербург: Профессиональная литература, АйТи-Подготовка, 2014. – 400 с.

4. Новицкий Н.И. Сетевое планирование и управление производством: Учебно-практическое пособие для ВУЗов. – Минск: Новое знание, 2004. – 159 с.