МЕЛЬНИК В.М.
Національний технічний
університет України «КПІ»
КОНСЕРВАТИВНІ СИСТЕМ. КОМП'ЮТЕРНИЙ РОЗРАХУНОК
ЧАСТОТНИХ ХАРАКТЕРИСТИК
Консервативні
системи, тобто системи, в яких відсутнє розсіювання
енергії, або, відповідно, з підживленням енергії
в міру її розсіювання, відрізняються
тією властивістю, що їх коливання, одного разу почавшись, не затухають. Тому, наприклад, експериментальне (за допомогою фізичного або математичного
експерименту) чисельне визначення їх частотних характеристик наштовхується на істотні труднощі. В той же
час, саме для подібних систем визначення їх частотних характеристик часто є абсолютно необхідними для дослідника, бо
саме такі системи особливо чутливо реагують на збурення на резонансних, або близьких до них, частотах. Можна, звичайно, отримати
аналітичний вираз для передаточної
функції об'єкта, замінивши в ній ![]() на
на ![]() і, тим самим, сформувати вирази для частотних
характеристик [1],
але для складних динамічних систем цей шлях надзвичайно громіздкий, а що стосується
систем з розподіленими параметрами, то він взагалі практично нереалізуємий
внаслідок виникаючих суто математичних труднощів. Разом з тим, методи
чисельного розрахунку перехідних процесів, орієнтовані на реалізацію їх на
сучасних комп'ютерах, зараз досить добре відпрацьовані [2]. При
необхідності обчислення, наприклад, вільних коливань багатомасової механічної
системи із зосередженими параметрами, або об'єкта з розподіленими параметрами,
особливих проблем не виникає. Маючи ж масив ординат вихідного сигналу об'єкта,
можна провести його спектральний аналіз і визначити для початку його власні (резонансні) частоти.
і, тим самим, сформувати вирази для частотних
характеристик [1],
але для складних динамічних систем цей шлях надзвичайно громіздкий, а що стосується
систем з розподіленими параметрами, то він взагалі практично нереалізуємий
внаслідок виникаючих суто математичних труднощів. Разом з тим, методи
чисельного розрахунку перехідних процесів, орієнтовані на реалізацію їх на
сучасних комп'ютерах, зараз досить добре відпрацьовані [2]. При
необхідності обчислення, наприклад, вільних коливань багатомасової механічної
системи із зосередженими параметрами, або об'єкта з розподіленими параметрами,
особливих проблем не виникає. Маючи ж масив ординат вихідного сигналу об'єкта,
можна провести його спектральний аналіз і визначити для початку його власні (резонансні) частоти.
Математичною базою спектрального аналізу є перетворення Фур’є
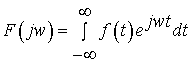 , (1)
, (1)
де ![]() є спектральна
характеристика функції
є спектральна
характеристика функції ![]() [3].
[3].
Її можна навести у у вигляді -
![]() , (2)
, (2)
де
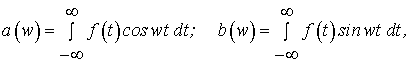
або, відповідно,
![]() , (3)
, (3)
Для практичної реалізації формул для ![]() і
і ![]() в (2) межі
інтегрування доводиться обирати від 0 до
в (2) межі
інтегрування доводиться обирати від 0 до ![]() (будемо
називати його часом спостереження процесу). Та обставина, що
(будемо
називати його часом спостереження процесу). Та обставина, що ![]() - скінченне, призводить до того, що визначається не дійсна спектральна характеристика (1), а,
так званий, поточний спектр. За
- скінченне, призводить до того, що визначається не дійсна спектральна характеристика (1), а,
так званий, поточний спектр. За ![]() він буде наближатись
до істинного. Якщо
він буде наближатись
до істинного. Якщо ![]() є періодичною
функцією, тоді
є періодичною
функцією, тоді ![]() в міру
зростання
в міру
зростання ![]() буде
наближатися до лінійчатого спектру, де екстремуми
будуть мати місце на частотах, що наближаються до власних частот об'єкта
(системи), якщо
буде
наближатися до лінійчатого спектру, де екстремуми
будуть мати місце на частотах, що наближаються до власних частот об'єкта
(системи), якщо ![]() відображає
вільний рух. Коли ж об'єкт, що досліджується, знаходиться під дією зовнішніх
впливів, тоді в його реакції
відображає
вільний рух. Коли ж об'єкт, що досліджується, знаходиться під дією зовнішніх
впливів, тоді в його реакції ![]() будуть присутні
періодичні компоненти, відповідні гармонічним складовим його входів.
будуть присутні
періодичні компоненти, відповідні гармонічним складовим його входів.
Зупинимося спочатку на визначенні резонансних частот консервативного об'єкта.
Якою величиною ![]() можна
обмежитися? Чим більше, тим краще? Так,
звичайно, але тут можливі проблеми з обсягом пам'яті, необхідної для зберігання
масиву ординат виходу об'єкта, з іншого боку, - зростає час формування
подібного масиву (особливо для складних розподілених об'єктів), а потім час
його обробки з обчисленням інтегралів за формулами (2) для досить широкого
діапазону частот. Пропонується алгоритм формування на екрані комп'ютера графіка
поточного спектра вихідного сигналу об'єкта в міру формування цього сигналу, що
позбавляє від необхідності накопичувати (зберігати) цей сигнал. Вважаємо, що
він формується або в процесі чисельного інтегрування відповідної системи
диференціальних рівнянь, що моделює об'єкт дослідження, або ж подається на
комп'ютер через відповідні перетворювачі від датчиків, встановлених на натурному
(фізичному) об'єкті. Обчислення інтегралів за формулою (2) починається з деякого початкового значення
можна
обмежитися? Чим більше, тим краще? Так,
звичайно, але тут можливі проблеми з обсягом пам'яті, необхідної для зберігання
масиву ординат виходу об'єкта, з іншого боку, - зростає час формування
подібного масиву (особливо для складних розподілених об'єктів), а потім час
його обробки з обчисленням інтегралів за формулами (2) для досить широкого
діапазону частот. Пропонується алгоритм формування на екрані комп'ютера графіка
поточного спектра вихідного сигналу об'єкта в міру формування цього сигналу, що
позбавляє від необхідності накопичувати (зберігати) цей сигнал. Вважаємо, що
він формується або в процесі чисельного інтегрування відповідної системи
диференціальних рівнянь, що моделює об'єкт дослідження, або ж подається на
комп'ютер через відповідні перетворювачі від датчиків, встановлених на натурному
(фізичному) об'єкті. Обчислення інтегралів за формулою (2) починається з деякого початкового значення ![]() (задається
користувачем), або навіть з
(задається
користувачем), або навіть з ![]() . Для того, щоб користувач отримав уявлення про характер
зміни
. Для того, щоб користувач отримав уявлення про характер
зміни ![]() на відрізку часу
на відрізку часу ![]() , на екран можна вивести графік
, на екран можна вивести графік![]() , а потім з інтервалом в
, а потім з інтервалом в ![]() кроків чисельного інтегрування (задає користувач) виводиться графік
кроків чисельного інтегрування (задає користувач) виводиться графік ![]() таким чином, щоб черговий
графік накладався на попередні і користувач мав можливість спостерігати
динаміку зміни
таким чином, щоб черговий
графік накладався на попередні і користувач мав можливість спостерігати
динаміку зміни ![]() в міру зростання часу
спостереження
в міру зростання часу
спостереження![]() . Користувачеві надається
можливість в будь-який момент часу звільнити екран, якщо там нагромадилося досить
багато кривих, які заважають оцінці останніх на поточний момент часу графіків
спектральної щільності. Користувач також може в довільному напрямі змінювати масштаб побудови графіка (в міру зростання t , висота піків на графіку зростає і
масштаб доцільно збільшити). Після
того як екстремуми, що цікавлять
користувача, оформились, з його точки зору, досить чітко, він може зупинити процес і надати графіку остаточного вигляду,
скориставшись можливостями, які надаються
для цього модулем GromU .
. Користувачеві надається
можливість в будь-який момент часу звільнити екран, якщо там нагромадилося досить
багато кривих, які заважають оцінці останніх на поточний момент часу графіків
спектральної щільності. Користувач також може в довільному напрямі змінювати масштаб побудови графіка (в міру зростання t , висота піків на графіку зростає і
масштаб доцільно збільшити). Після
того як екстремуми, що цікавлять
користувача, оформились, з його точки зору, досить чітко, він може зупинити процес і надати графіку остаточного вигляду,
скориставшись можливостями, які надаються
для цього модулем GromU .
Отже, маючи процедуру Specter, можна вважати
задачу визначення вільних частот об'єкта вирішеною. Зупинимося на розрахунку частотних характеристик консервативних систем.
Розглянемо спочатку метод, який полягає в застосуванні
формул [4, 5]
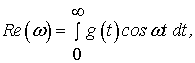 (4)
(4)
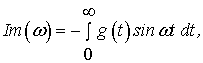 (5)
(5)
де ![]() - імпульсна
характеристика (функція ваги) каналу об'єкта, що вивчається,
- імпульсна
характеристика (функція ваги) каналу об'єкта, що вивчається, ![]() і
і ![]() - дійсна та
уявна частотні характеристики.
- дійсна та
уявна частотні характеристики.
Імпульсну характеристику вважаємо відомою, заданою у вигляді масиву
її ординат.
Цей метод досить ефективний за умови, коли
імпульсна характеристика швидко затухає, тобто якщо для ![]() вона практично
дорівнює нулю. Тоді верхня межа інтегрування в (4), (5) замінюється на
вона практично
дорівнює нулю. Тоді верхня межа інтегрування в (4), (5) замінюється на ![]() , і застосування
відповідного алгоритму чисельного
інтегрування вирішує задачу.
, і застосування
відповідного алгоритму чисельного
інтегрування вирішує задачу.
Однак, саме для консервативних систем ![]() . Інтегрувати ж в нескінченних
межах на комп'ютері немає змоги.
. Інтегрувати ж в нескінченних
межах на комп'ютері немає змоги.
References
1. Karachun, V. The
additional error of inertial sensors induced by hypersonic flight conditions [Текст]/ V. Karachun, V. Mel’nick, I. Korobiichuk, M.
Nowicki, R. Szewczyk, S. Kobzar// 2016; Sensors (Switzerland). Volume: 16. Issue: 3. Year: 2016-02-26. EID: 2-s2.0-84959187681. Scopus ID: 84959187681. DOI: 10.3390/s16030299.
2.
Mel’nick, V. The
emergence of resonance within acoustic fields of the float gyroscope suspension
[Текст]/ V. Mel’nick, V. Karachun //
EasternEuropean Journal of Enterprise Technologies. ISSN: 17293774. Volume: 1.
Issue: 7. Pages: 39-44. Year: 2016-01-01. EID: 2-s2.0-84960858488. Scopus ID:
84960858488. DOI: 10.15587/1729-4061.2016.59892
3.
Karachun, V.V. Elastic stress state of a floating-type suspension in the
acoustic field. Deviation of the spin axis [Текст]/ V.V. Karachun, V.N. Mel’nik // Strength of
Materials. ISSN:
00392316. Volume: 44. Issue: 6. Pages: 668-677. Year: 2012-11-01. EID:
2-s2.0-84961216138. Scopus ID: 84961216138. DOI: 10.1007/s11223-012-9421-2.
4. Mel'nik, V.N.
Stress-strain state of a gyroscope suspension under acoustic loading [Текст]/ V.N. Mel’nik //
2007;
Strength
of Materials. ISSN: 00392316. Volume: 39. Issue: 1. Pages: 24-36. Year:
2007-01-01. EID: 2-s2.0-34147198666. Scopus ID: 34147198666. DOI:
10.1007/s11223-007-0004-6.
5. Mel'nik, V.N.
Influence of acoustic radiation on the sensors of a gyrostabilized platform [Текст]/ V.N. Mel’nik, V.V. Karachun// 2004; Prikladnaya Mekhanika. ISSN:
00328243. Volume: 40. Issue: 10. Pages: 122-130. Year: 2004-12-01. EID:
2-s2.0-14844342416. Scopus ID: 14844342416.