Технические науки/Отраслевое машиностроение

Рубашка В.П.

Украинская инженерно-педагогическая академия, г. Харьков

Дискретная модель упругой мостовой системы

с подвижной массой.

Анализ совмещенных режимов работы механизмов грузоподъемных машин мостового типа показал, что одна из отличительных особенностей динамического нагружения заключается в нестационарности их упругих и инерционных свойств. Изменение физических параметров во времени вызывается непосредственно характером выполняемых перегрузочных операций, связанных с относительным перемещением дискретных элементов упругой модели, и является неотъемлемой частью единого колебательного процесса, развивающегося в любом кране мостового типа. В первую очередь это относится к нестационарным колебаниям, обусловленным движением тележки в пролете крана мостового типа. При этом происходит не только дополнительные нагружения металлоконструкции в вертикальной плоскости за счет перемещения инерционной нагрузки, но и определяемое этим перераспределение жесткостных и инерционных параметров всей упругой системы.

В настоящее время нет детальных исследований рассматриваемых динамических явлений. В работах, посвященных изучению колебаний подъемно-транспортных машин, как правило, принимается, что движение тележки происходит по абсолютно жесткому мосту [1,2]. С другой стороны, известные в теории механических колебаний методы анализа воздействия подвижных инерционных нагрузок на динамику элементов упругих конструкций [3,4,5] не учитывают свойств применяемых в подъемно-транспортном машиностроении рабочих механизмов и способов управления ими, так как ориентированы на модели с заранее известным законом изменения скорости перемещаемых масс.

В данном же случае, мы имеем механическую систему, дискретное включение которой движется под воздействием нестационарного внешнего усилия, развиваемого приводным механизмом. Причем, исследования, проведенные в работе [6] показали, что этот процесс определяется не только параметрами электропривода, но и уровнем колебаний несущей конструкции. Таким образом, перемещение дискретной массы, с одной стороны влияет на динамические свойства упругой модели с другой стороны, поставлено в зависимость от них.

Следовательно, возникает необходимость совместного решения уравнений движения массы и колебаний упругого объекта, являющихся звеньями единой нестационарной системы. Считается, что подвижная нагрузка в каждый момент времени разбивает пролет несущего строения на элементы переменной длины. Для получения решений вводятся нестационарные дискретные модели, которыми представляются элементы переменной длины. В качестве метода дискретизации выбран метод конечных элементов, преимущества которого в определении параметров дискретной схемы наиболее ярко проявляются для систем с зависимыми во времени свойствами.

В качестве объекта исследований рассмотрим мостовую конструкцию с постоянными по длине значениями жесткости , погонной массы и произвольными условиями опирания концов. Система несет массу , положение которой в пролете характеризуется координатой . Вид модели представлен на рис. 1.

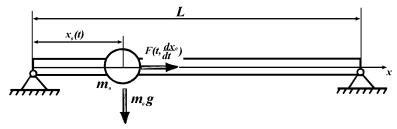
Рис. 1. Модель мостовой конструкции с подвижной массой

Из характера внешнего силового нагружения видно, что масса перемещается под воздействием нестационарного усилия , величина которого в общем случае может зависеть не только от времени, но и от скорости движения дискретного включения, а также уровня его колебаний вместе с несущей упругой конструкцией. В этом состоит основное отличие данной задачи от классической постановки, где задается не движущая сила, а закон изменения скорости тела, что не всегда точно отражает реальные условия его передвижения.

С целью построения математической модели, описывающей колебания системы, будем считать, что в каждый момент времени подвижная масса разбивает пролет на два участка с переменной во времени длинной.

Представим конструкцию конечно-элементной моделью с постоянным числом узлов дискретизации. Разбиение на конечные элементы проводится таким образом, чтобы первый и последний узлы совпадали с точками опор моста, а один из промежуточных узлов – с положением подвижной массы мо в данный момент времени.

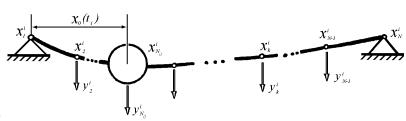
Рис. 2. Конечно - элементная модель моста для момента времени .

В работе [6] приведена система уравнений, описывающих поведение системы мост – подвижная инерционная нагрузка. Из этой системы уравнений для момента времени определяются упругие перемещения моста и новое текущее положение подвижной массы .

Это новое положение подвижной массы является основой для введения новых узлов дискретизации где первый и последний совпадают по-прежнему с опорами моста, а некоторый промежуточный – с новым положением подвижной массы .

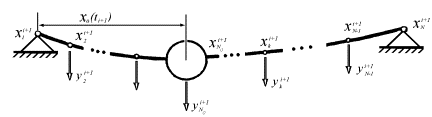
Рис. 3. Конечно - элементная модель моста для момента времени

Динамика такой системы описывается системой уравнений аналогично той, которая соответствовала предыдущему моменту времени только относительно уже новых неизвестных, которые характеризуют прогибы моста в новых точках дискретизации и нового положения подвижной массы.

Следует отметить, что такая схема позволяет рассматривать значительно более широкий класс задач, связанных не только с изучением колебаний несущей конструкции, но и характером передвижения по ней сосредоточенной инерционной нагрузки.

Литература:

1. Хиценко А.И. Моделирование колебаний груза при перемещении тележки мостового крана / А.И. Хиценко, С.Р. Бежин // Машинознавство. Матеріали 13 регіональної науково-методичної конференції. Донецьк: ДонНТУ, 2010.

2. Ловейкин В.С. Оптимизация переходных режимов движения механизма передвижения тележки грузоподъемных машин / В.С. Ловейкин, В.Ф. Ярошенко // Вестник Харьковского национального технического университета сельского хозяйства имени Петра Василенка. – 2007. – 460 с

3. Глухов Ю.П.Динамика многослойной предварительно напряженной плиты на жестком основании при воздействии подвижной нагрузки [Текст] / Ю. П. Глухов // Доповіді Національної академії наук України. - 2012. - N 2. - С. 70-75.

4. Архипенко Юрий Васильевич. Методика расчета динамического взаимодействия подвижных нагрузок с мостами с применением программных комплексов конечно-элементного анализа : дис. канд. техн. наук : 05.23.11 Москва, 2006 176 с. РГБ ОД, 61:07-5/469

5. Облакова Т.В. О резонансном режиме в нестационарной задаче о подвижной нагрузке для упругого полупространства. Инженерный журнал: наука и инновации. №9, 2013.

6. Рубашка В.П. Математическая модель мостовой конструкции с подвижным инерционным включением.// Материалы ІІІ Международной научно-практической конференции «Эффективные инструменты современных наук – 2007». Технические науки. –Днепропетровск: Наука и образование, 2007.