магистрант 2 года Алибекова Ж., к.т.н., доцент Балабеков Б.Ч.

Южно-Казахстанский Государственный Университет имени М. Ауезова, г. Шымкент, Казахстан

Скалярная визуализация при физическом моделировании

Одним из приложений компьютерной графики является визуализация результатов научных исследований /1/, которую можно определить как преобразование массива данных в графические образы при помощи методов компьютерной графики. При выполнении научной работы данные могут быть получены из множества источников: результаты эксперимента, результаты математического моделирования или имитационного моделирования. При этом графическое представление данных позволяет наглядно увидеть большие массивы чисел, обнаружить в этих массивах наиболее интересные подмножества и уделить дальнейшее внимание в исследовании именно им. Создание графического образа и составляет суть процесса визуализации данных. При физическом моделировании, обычно, возникает задача оценки распределения некоторой величины процесса в объеме. Причем эта величины может быть скалярной, векторной или тензорной величиной по своей природе. В данной работе мы ограничиваемся случаем скалярной величины, выраженной функцией от двух переменных.

Визуализация функции от двух переменных представляет собой одну или несколько поверхностей в трехмерном пространстве на основе координатной сетки, при этом зависимая переменная графически представляется как высота соответствующей точки над уровнем координатной плоскости ху. Результаты топографической съемки являются примером подобной формы представления.

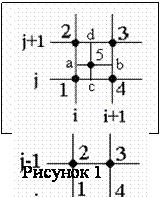
Трехмерное изображение поверхности не позволяет получить количественную оценку значений функции в отдельных точках или в окрестности точки. Для этого необходимо исследуемую функцию представить на двухмерной плоскости линиями уровня, которые соответствуют фиксированным значениям функции. Здесь появляются две задачи. Первая задача заключается в нахождении линий уровня для известных значений функции. Рассмотрим регулярную сетку с квадратными ячейками в декартовой системе координат с независимыми переменными x и y (рисунок 1):

x_i = x₀ + iΔx, i = 1, … , N,

y_i = y₀ + jΔy, j = 1, … , M, (1)

Δx = Δy.

На этой сетке заданы значения функции f(x_i, y_j). При нахождении линий уровня этой функции нужно найти решение уравнения

f(x_i, y_j) = p. (2)

В общем случае ищут кусочно-линейную аппроксимацию линии уровня. При прохождении линии уровня через ячейку может оказаться, что ни одно из значений функции в узлах ячейки не будет равно значению р из (2). Обозначим значения функции как f1, f2, f3, f4 в соответствующих узлах ячейки (рисунок 1). Тогда возможных только четыре варианта для отношения между множеством { f1, f2, f3, f4 } значением р:

1) f1 < p, f2 < p, f3 < p, f4 < p, 2) f1 > p, f2 < p, f3 < p, f4 < p,

3) f1 > p, f2 < p, f3 < p, f4 > p, 4) f1 > p, f2 < p, f3 > p, f4 < p.

Графическое представление этих случаев показано на рисунке 2.

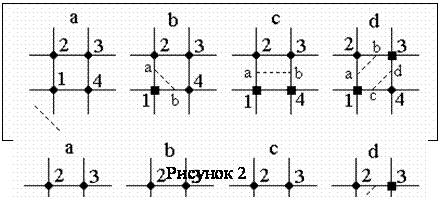
Для первого варианта линия уровня не пересекает ячейку. Для остальных вариантов можно записать следующие пропорции:

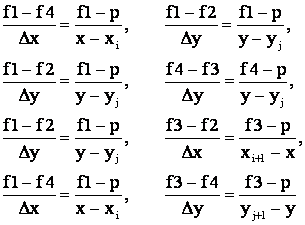(3)

Из этих соотношений можно получить выражения для координат точек пересечения линий уровня с ребрами ячеек. Для 2-го варианта (рисунок 2b) имеем.

Координаты точки а

(4)

Координаты точки b

(5)

Для 3-го варианта (рисунок 2c) имеем. Координаты точки а определяются по формулам (4). Координаты точки b

(6)

Для 4-го варианта (рисунок 2d) имеем. Координаты точки а определяются по формулам (4). Координаты точки с определяются по формулам (6). Координаты точки b

(7)

Координаты точки d

(8)

Формулы (4) – (8) являются исходными данными при разработке компьютерной программы построения линий уровня.

Вторая задача заключается в нахождении значений функции в межузловом пространстве при известных значениях функции в узлах ячейки сетки. Значение функции в точке 5 на рисунке 1 c координатами

x = x_i + dx, y = y_j + dy (9)

определяется линейной аппроксимацией следующим образом. Предварительно находят значения функции в дополнительных точках a, b, c, d на рисунке 1.

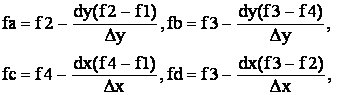(10)

Тогда значение f5 можно определить по формулам

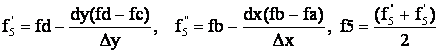(11)

Полученные выражения полностью решают поставленные задачи и позволяют разработать соответствующее программное обеспечение.

Литература

1. Эйнджел Э. Интерактивная компьютерная графика. – М.: Издательский дом “Вильямс”, 2001. - 592 с.