Технические системы
Автоматизированные системы управления на производстве
Айтчанова Ш.К.
Республика Казахстан, Алматинский институт энергетики и связи
ФУНКЦИОНАЛЬНЫЕ РЯДЫ В ТЕОРИИ
СТОХАСТИЧЕСКИХ НЕЛИНЕЙНЫХ СИСТЕМ
Широкий класс стохастических систем относится
к классу нелинейных динамических систем и представляется функциональным
уравнением [1]
![]() , (1)
, (1)
где u(t) – входной случайный процесс; z(t) - выходной
случайный процесс; параметр l
характеризует случайность нелинейного преобразования, представляемого
функционалом G.
При
изучении систем (1) случайность их параметров удобно представить в виде
дополнительного внешнего возмущения действующего на параметры системы [2]. В
этом случае уравнение (1) записывается в виде
![]() ,
(2)
,
(2)
Целью
настоящей работы является построение общей формы функционала в виде рядов
Вольтерра, представляющего решение уравнения типа (1) и описывающего поведение
стохастических нелинейных систем.
Рассматривается
стохастическая динамическая система, представляемая уравнением (2). Известно, что для многих
систем автоматического управления в рабочих зонах их амплитудно-частотной
характеристики спектральные плотности возмущающих воздействий на параметры
остаются постоянными. Это дает возможность считать случайные возмущения m(t) в уравнении (2) белым шумом с характеристиками:
![]()
![]() ,
(3)
,
(3)
где r11-интенсивность (высота) спектральной
плотности белого шума.
Выразим
белый шум m(t) через соответствующий ему винеровский процесс ![]() [3]
[3]
![]() ,
(4)
,
(4)
или
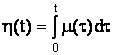 , (5)
, (5)
где h(t)-траектории винеровского процесса H(t),
удовлетворяющего соотношениям:
![]() ,
,![]() . (6)
. (6)
С
учетом (4) представим при нулевых начальных условиях решение уравнения (2) в
виде следующего функционала
![]() .
(7)
.
(7)
В
(7) траектории u(t) и h(t) входного процесса u(t) и шума h(t) удовлетворяют условиям ограниченности в вероятностном смысле, например:
![]() , (8)
, (8)
![]() . (9)
. (9)
Функционал
А является непрерывным в вероятностном смысле, например, для любых функций u1(t), u2(t) из u(t) и h1(t),h2(t) из h(t) существуют сколь угодно малые положительные числа g, d(g), e, b(e) для которых справедливо:
![]()
![]() .
(10)
.
(10)
В
этом случае справедливо следующее утверждение.
Утверждение.
Если функционал (7) является непрерывным в вероятностном смысле, а входные
процессы u(t) и ![]() удовлетворяют
условиям ограниченности в вероятностном смысле (8) и (9), то он может быть
представлен в виде следующего ряда
удовлетворяют
условиям ограниченности в вероятностном смысле (8) и (9), то он может быть
представлен в виде следующего ряда
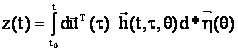 ,
(11)
,
(11)
где матрица ![]() определяется
в виде
определяется
в виде
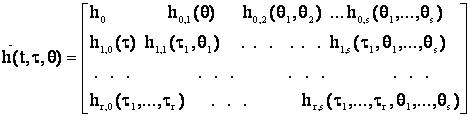 , (12)
, (12)
вектора
![]() и
и ![]()
![]() ;
;
![]() . (13)
. (13)
Интеграл
при импульсной характеристике ![]() имеет кратность, равной r+s. Через t и q обозначены комбинации (t1,…,tr) и (q1,….,qs), которые
раскрываются в соответствии с правилами обычного каскадного соединения. Интегралы
при дифференциале du(t) понимаются как среднеквадратические интегралы
Стилтьеса, а при дифференциале d*h(q)- как среднеквадратические
интегралы Ито.
имеет кратность, равной r+s. Через t и q обозначены комбинации (t1,…,tr) и (q1,….,qs), которые
раскрываются в соответствии с правилами обычного каскадного соединения. Интегралы
при дифференциале du(t) понимаются как среднеквадратические интегралы
Стилтьеса, а при дифференциале d*h(q)- как среднеквадратические
интегралы Ито.
Доказательство.
Следуя методике, использованной в [1], рассмотрим вместо реальных входных
процессов u(t) и ![]() (t) их
ступенчатые аппроксимации
(t) их
ступенчатые аппроксимации
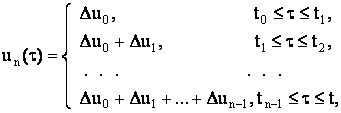 (14)
(14)
где ![]() .
.
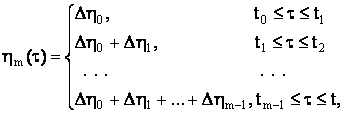 (15)
(15)
где ![]() .
.
степень приближения последовательностей
ступенчатых процессов un(t) и ![]() m(t) к соответствующим реальным случайным процессам u(t) и
m(t) к соответствующим реальным случайным процессам u(t) и ![]() (t) может оцениваться в смысле
(t) может оцениваться в смысле
![]() ,
, ![]() .
.
Последовательность ступенчатых функций (14) и (15)
приближается к соответствующим входным процессам, если
![]() .
.
Если теперь на вход системы подать процессы un(t) и ![]() m(t), состоящие из ступенчатых функций (14) и (15), то
функционал (7) будет зависеть от Du0, Du1,..., Dun-1,
m(t), состоящие из ступенчатых функций (14) и (15), то
функционал (7) будет зависеть от Du0, Du1,..., Dun-1, ![]() , т.е. вместо функционала
получим функцию n+m переменных:
, т.е. вместо функционала
получим функцию n+m переменных:
![]() . (16)
. (16)
Наряду с функцией n+m переменных (16) рассмотрим полиномы
вида
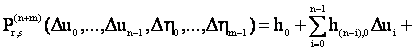
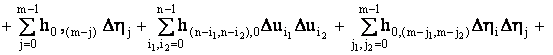
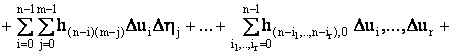
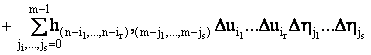 . (17)
. (17)
Функцию А (n+m) (16) будем описывать
с помощью полиномов P(n+m)r,s (17) в смысле
![]() .
.
Теперь осуществим предельный переход от
функций (16) к функционалу (7), т.е.
![]() .
.
Для этого рассмотрим смысл предельного
перехода каждых элементов полинома (17). В него входят интегральные суммы двух
видов. В одну из них входят приращения входного процесса u(t) в виде ![]() , а в другую –
, а в другую –![]() (t) в виде
(t) в виде ![]() .
.
Интегральная
сумма первого типа в линейном случае имеет вид
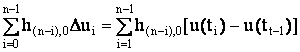 . (18)
. (18)
Из-за непрерывности исходной функции А(n+m) ступенчатая функция hn,0(t), образованная из чисел h(n-i),0 i=1,2,..,n-1, сходится к
непрерывной функции h1,0(t),т.е.
![]() .
(19)
.
(19)
Входной
процесс u(t) с вероятностью
единица имеет ограниченную вариацию. В этом случае пределом интегральной суммы
(19) в среднем квадратичным будет интеграл Стилтьеса [1], т.е.
![]() . (20)
. (20)
Аналогично, предел в среднем квадратичном рассматриваемого вида
интегральной суммы r-го порядка ![]() примет вид
примет вид
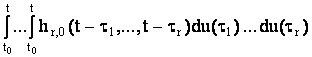 . (21)
. (21)
Теперь рассмотрим интегральную сумму второго
вида. В линейном случае она имеет вид
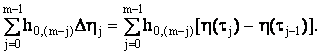 (22)
(22)
Аналогично, предел
ступенчатой функции ![]() определяется в смысле
(19).
определяется в смысле
(19).
В отличие от (19),
входной процесс ![]() (t), входящий в рассматриваемую
сумму (22), имеет неограниченную
вариацию. Тем не менее, предел в среднем квадратичном интегральной суммы (22)
существует и носит название стохастического интеграла Ито [2]:
(t), входящий в рассматриваемую
сумму (22), имеет неограниченную
вариацию. Тем не менее, предел в среднем квадратичном интегральной суммы (22)
существует и носит название стохастического интеграла Ито [2]:
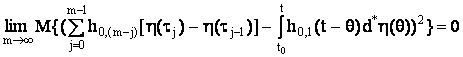 . (23)
. (23)
Стохастические интегралы,
понимаемые в смысле Ито, обозначаются далее звёздочкой при дифференциале ![]()
Аналогично, предел в
среднем квадратичном
рассматриваемого вида
интегральных сумм s-го порядка 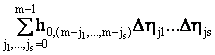 примет вид
примет вид
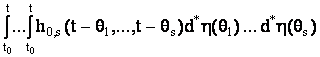 . (24)
. (24)
В результате, совершая
предельный переход от функций ![]() (16) к функционалу А
(7) с учетом полученных видов интегральных функционалов (20), (21) и (22), (23), получим общую форму нелинейного
стохастического функционала (7), которая в векторно-матричных обозначениях (12),
(13) примет вид (7). Утверждение доказано.
(16) к функционалу А
(7) с учетом полученных видов интегральных функционалов (20), (21) и (22), (23), получим общую форму нелинейного
стохастического функционала (7), которая в векторно-матричных обозначениях (12),
(13) примет вид (7). Утверждение доказано.
Таким образом, получено
описание типа “вход-выход” нелинейных динамических систем со случайными
параметрами в виде функционала (7). Ряд (7) будем называть стохастической
вольтерровской моделью системы вида (2).
Такое
описание стохастических нелинейных динамических систем в виде функционала (7)
позволяет исследовать основные его свойства, такие как оценка динамической
точности, статистический синтез и др.
Литература:
1. Попков Ю.С., Киселев
О.Н., Петров Н.П., Шмульян Б.Л. Идентификация и оптимизация нелинейных
стохастических систем. М.: Наука,1976, 438 с.
2. Тихонов В.И., Миронов
В.А. Марковские процессы. М.: Сов. радио, 1977,
488 с.
3. Тихонов
В.И.Статистическая радиотехника. М.: Сов. радио, 1966, 678 с.