Экономика/ 4. Инвестиционная деятельность и фондовые рынки

Андриенко В.М., Варчук О.В.

Одесский национальный политехнический университет

Фрактальные свойства фондовых рынков

 Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому" [1]. Это определение не является математически строгим. Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. Свойство самоподобия является качественным, то есть объект или процесс являются подобными в различных масштабах, пространственных или временных, статистически. Каждый масштаб напоминает другие масштабы, но не идентичен им. Отдельные ветви дерева качественно самоподобны другим ветвям, но каждая ветвь является также уникальной. Это свойство делает фрактал масштабно-инвариантным.
 Вторым свойством фракталов является фрактальная размерность, которая может описывать либо физическую структуру, либо временной ряд. Фрактальная размерность характеризует то, как предмет заполняет пространство. Кроме того она описывает структуру предмета при изменении коэффициента увеличения или при изменении масштаба предмета. Для физических или геометрических фракталов такой закон подобного преобразования имеет место в пространстве. Фрактальный временной ряд изменяет масштаб статистически, во времени. Фрактальная размерность 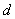 временного ряда определяет степень его зазубренности. Прямая линия имеет фрактальную размерность, равную единице (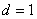), а случайный временной ряд - 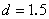. При значениях  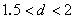временной ряд более зазубрен, чем случайная последовательность, или имеет больше инверсий. Статистика временного ряда с фрактальными размерностями, отличными от 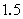, не обязательно находится в пределах нормального распределения.
 Эйнштейн, изучая броуновское движение, обнаружил, что расстояние, которое проходит случайная частица, увеличиваеся пропорционально корню квадратному из времени, за которое она проходит это расстояние: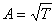
  , (1)
где 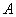 - пройденное расстояние,
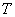  - время, за которое пройдено расстояние .
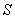В финансовой экономике эта формула используется для пересчета волатильности на период времени 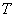 по известной волатильности за период . 
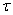  (2)

Эта формула предполагает, что дисперсия доходностей фондовых активов увеличивается как квадратный корень из времени. К сожалению формула (2) неверна практически для всех финансовых рынков и не описывают их существенные свойства: наличие памяти и склонность к большим выбросам. Эти свойства рынка могут быть учтены в модели фрактальной природы рынков [1]. Фрактальная модель утверждает, что рынки самоподобны на различных временных масштабах, а волатильности, вычисленные на базе разных временных интервалов соотносятся друг с другом по следующей формуле:

(3)

Показатель степени H называется показателем Херста. Известный британский гидролог Х.Е. Херст предложил метод нормированного размаха (  анализ), позволяющий различить случайный временной ряд и фрактальный. - анализ является простым процессом, который требует переработки большого количества данных. Рассмотим последовательность шагов вычислительного процесса[ 2 ]:

1. Пусть ( ) – ряд котировок некоторой ценной бумаги (в общем случае – временной ряд). Образуем из данного ряда последовательность () - логарифм доходности.

2. Разобъем последовательность на смежных последовательностей одинаковой длины , . Обозначим через элементы -ой последовательности .

3. Для каждой последовательности вычислим:

- среднее значение и стандартное отклонение ее элементов соответственно по формулам , ;

- накопленные суммы , ;

- размах накопленных сумм , , ;

4. Для разбиения на подпоследовательности длины вычисляем нормированный размах накопленных сумм .

Далее производят новое разбиение на подпоследовательности большей длины и шаги 1-4 повторяют до . Например, для последовательности из 200 данных возможны такие варианты разбиения: ; ; ; ; . Отметим, что значения производят нестабильные оценки при небольших объемах выборки, поэтому рекомендуется использовать . Таким образом, будет получено несколько значений для различных . Размах является расстоянием , на которое перемещается система за время . Херст обнаружил более общую форму уравнения (1)

, (4)

где - константа. Значение изменяет масштаб по мере увеличения приращения времени согласно значению степенной функции, равному , то есть диапазон увеличвается согласно степени. Это называется масштабированием со степенной зависимостью, что является характерной чертой фракталов. Логарифмируя равенство (4), получим уравнение прямой (5) в координатах (,. График приведен на Рисунке 1.

(5)

Показатель Херста–это тангенс угла наклона прямой (5) к оси (Рисунок 1).

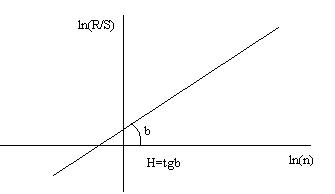
Рисунок 1 – Интепретация показателя Херста.

Оценку показателя Херста вычислим по данным, полученным в результате выполнения шагов 1- 4, применяя метод наименьших квадратов. Пусть произведено 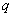 вариантов разбиения последовательности 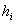. Обозначим  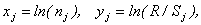где 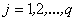. Тогда по методу наименьших квадратов оценка показателя  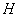равна
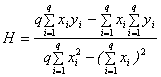  (6)
 Значение 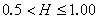 подразумевает персистентный временной ряд, а такой ряд характеризуется эффектами долговременной памяти. Теоретически это означает: то, что происходит сегодня , воздействует на будущее. Такая долговременная память имеет место независимо от масштаба времени: все ежедневные изменения соотносятся со всеми будущими ежедневными изменениями, все еженедельные изменения соотносятся со всеми будущими еженедельными изменениями. Не существует характерного масштаба времени, ключевой характеристики фрактального временного ряда. Персистентный временной ряд является самым распространенным типом,встречающимся в природе. Он также является самым распространенным и в экономике , и на фондовых рынках.
 Значение  означает антиперсистентность. Антиперсистентная система проходит меньшее растояние, чем случайная система. Чтобы система прошла меньшее расстояние, она должна меняться чаще, чем вероятностный процесс. 
  Значение  соответствует обычному белому гауссовскому шуму  , случайному блужданию броуновской частицы, то есть процессу полностью лишенному памяти.
 Описанный подход был применен для исследования динамики акций на ММВБ нескольких росссийских компаний. Вычисленный показатель Херста оказался для всех компаний больше 0.5( Таблица 1).
 Таблица 1
Значения показателя Херста 

Наименование компании	Аэрофлот	Газпром	Лукойл	Камаз
Показатель Херста	0,64	0,71	0,58	0,68

Как видно из таблицы, анализируемые показатели обладают фрактальными свойствами, то есть являются персистентными временными рядами с долговременной памятью.

Обозначим ( ) – ряд котировок некоторой ценной бумаги. Образуем из данного ряда последовательность

. (7)

Цены закрытия вычисляются на следующем торговом интервале по формуле:

(8)

Выражение для разделим на две части: среднее значение и случайную величину ε_i, подчиняющуюся искомому статистическому распределению с нулевым средним значением:

(9)

Рассмотрим случайный процесс (10)[3]

, , (10)

где -случайная величина, распределенная по нормальному закону с нулевым средним значеним и среднеквадратическим отклонением , = 1 при любом показателе , – гамма-функция, которая определяется формулой

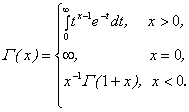(11)

Для целых неотрицательных значений аргумента

, (12)

По существу, формула (10) представляет собой свертку процесса Гаусса с бесконечным рядом, то есть бесконечное скользящее среднее процесса Гаусса, моделирующее процесс с памятью ARIMA(0,d,0), где . Гамма-функция может быть вычислена приближенно по формуле Стирлинга

(13)

Полученный по формуле (10) случайный процесс обладает следующими свойствами: нулевым средним, как и процесс , тем же среднеквадратичным отклонением , что и процесс , фрактальностью и памятью при . Процесс (10) используем для прогнозирования цен акций для названных выше компаний (Таблица 2). Данные Таблицы 2 свидетельствуют об адекватности модели (10). Несколько хуже результат моделирования для компании «Камаз», однако среднеквадратическая ошибка меньше среднеквадратического отклонения (11,33 против 24,25). Следовательно, и в данном случае можно считать данные , полученные на модели в достаточной степени адекватными реальным данным.

Таблица 2

Результаты моделирования

Аэрофлот		Газпром		Лукойл		Камаз
Факт	Прогноз	Факт	Прогноз	Факт	Прогноз	Факт	Прогноз
94.12	94.31	352.69	353.16	2 079.00	2078.651	131.50	128.75
95.39	95.51	352.40	352.89	2 062.00	2063.116	142.99	134.66
95.76	95.95	355.91	356.48	2 036.00	2035.139	144.19	141.44
96.99	97.15	363.70	364.39	2 004.00	2001.492	152.00	146.78
98.30	98.39	360.24	360.74	1 990.97	1988.644	161.99	153.21
96.55	96.88	342.45	342.82	1 892.00	1891.459	173.00	153.52
95.00	95.12	331.04	332.23	1 891.00	1891.253	166.75	151.53
93.87	93.87	327.05	326.70	1 870.00	1867.961	154.10	142.39
89.75	89.86	303.80	303.21	1 718.00	1716.005	143.00	136.51
88.49	88.48	307.00	306.53	1 666.00	1666.597	142.90	128.26
86.00	86.12	296.00	295.74	1 600.00	1599.963	143.00	128.22
90.79	90.93	307.20	307.60	1 736.99	1739.678	150.00	134.87
92.70	92.77	316.23	316.70	1 818.00	1818.956	146.50	141.11
Среднеквадратичская ошибка 0.13		Среднеквадратичская ошибка 0.53		Среднеквадратичская ошибка 1.59		Среднеквадратичская ошибка 11.33

Благодаря развитию компьютерных технологий созданы программы, с помощью которых стало возможным моделирование процессов с фрактальными свойствами, например, свободно распространяемый пакет Fractan 4.4 (http://soft.softodrom.ru/ap/Fractan-p44195). Для моделирования в пакете Fractan требуется более трех тысяч эмпирических данных. Приведенные выше результаты позволяют сделать следующие выводы. Для успешной работы на финансовых рынках необходимо владеть надёжными методами анализа и прогнозирования изменения цен и доходностей различных инструментов. Качество прогноза зависит от свойств прогнозируемого ряда, поэтому прогнозу всегда должен предшествовать всесторонний анализ.

Литература

1. Федер Е. Фракталы. Пер. с англ.-М.: Мир,1991.-254с.

2. Э.Петерс Фрактальный анализ финансовых рынков.-М.: «Интернет-Трейдинг» , 2004.-304с.

3. М.М. Леоненко, Ю.С. Мішура, В.М.Пархоменко, М.Й.Ядренко. Теоретико-ймовірнісні та статистичні методи в економетриці та фінансовій математиці.-К.:Інформтехника,1995.-380с.