УДК 517.928.4:517.929.4

Технические науки/2.Механика

к.т.н. Дюсембина Ж. К.

Алматинский технологический университет, Казахстан

Математические модели популяционной динамики

Математические модели популяционной динамики и стабилизация движения на основе теории Т-устойчивости и Т - управляемости для случая n=3, где имеет место самолимитирование первого вида среди популяций n видов.

_{Рассмотрим функцию Ляпунова вида}

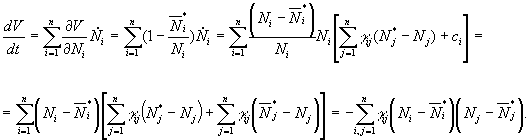₍₁₎

_{и предположим, что величина образуют антисимметрическую матрицу, т.е.}

₍₂₎

_где

_,

_то

₍₃₎

_{Если , то это значит, что - й вид увеличивается за счет - го вида, в то время как при -й вид сокращается в пользу - го вида.}

_{Управление заменим на}

₍₄₎

_Тогда

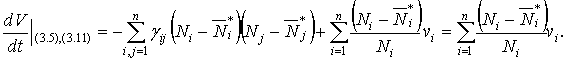₍₅₎

_{Положим}

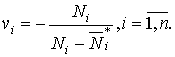₍₆₎

_{При этом}

_{Заметим, что если то потребуется, чтобы было}

_{При управлении}

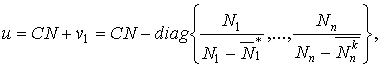₍₇₎

_{для системы}

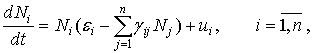₍₈₎

_{имеет место - управляемость, так как не регулируемая часть системы}

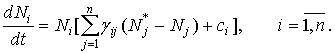₍₉₎

_{устойчива по Ляпунову. Следовательно, управление (7) осуществляет перевод системы (8) из положения равновесия в желаемое положение , причем время перевода:}

_при

_{т.е. (10)}

_{согласно общей теореме о - управляемости и - устойчивости.}

_{Рассмотрим подход теории устойчивости на конечном отрезке времени. Пусть . Тогда уравнения в отклонениях системы (8) примут вид:}

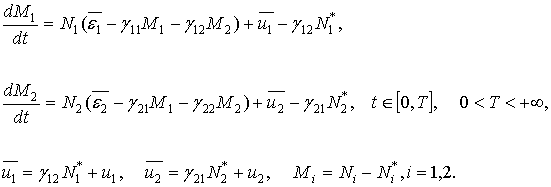₍₁₁₎

_{Линейно-однородная часть системы имеет вид:}

₍₁₂₎

_{Фундаментальная матрица решений системы (12) определяется из уравнения:}

_и

_{так как}

_{Вычислим матрицы}

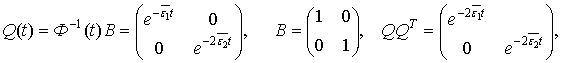
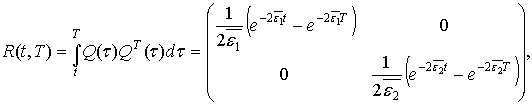
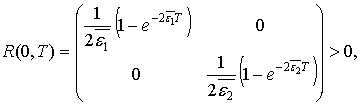
_если

_Далее,

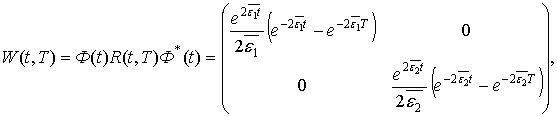
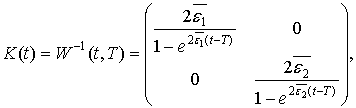
_т.е.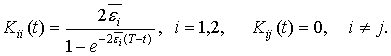

_{Тогда для системы}

_{управляемость обеспечивается управлением вида: .}

_{Систему (9) можно представить в виде:}

₍₁₃₎

_где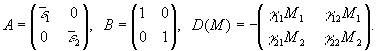

_{управление имеет вид:}

₍₁₄₎

_{где вектор-функция равна}

_{и матрица такая, что}

_{Учитывая, что}

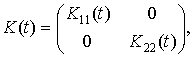
_имеем

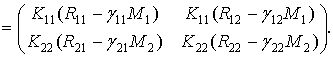
_{Положим , тогда}

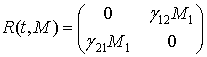
_{и управление (14) примет вид:}

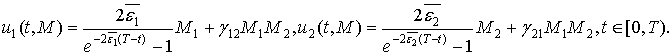_{При этом согласно теореме об устойчивости движения на конечном отрезке времени}

_{Отметим, что можно рассмотреть различные другие варианты стабилизации движения на конечном отрезке времени и обобщенное уравнение в виде системы (8).}

Литература:

1. Бияров Т.Н. Об устойчивости нелинейных систем на конечном отрезке времени // Стабилизация и оптимальное управление динамических систем. – Алма-Ата: Изд-во КазГУ. – 1988.

2. Четаев Н.Г. Устойчивость движения. – М.: Наука, 1990.

3. Свирежев Ю.М., Елизаров Е.Я. Математическое моделирование биологических систем. – М.: Мир. 1972.