построение 3D графиков на основе шести ПЕРЕМЕННЫХ

Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

В данной статье рассмотрен вопрос влияния шести переменных на ВВП (GDP) и представление их в виде 3D рисунков. Эти рисунки позволяют представить влияние различных переменных на ВВП (GDP). То есть, в статье рассмотрена зависимость изменения ВВП (GDPeu) = f(Х1,Х2, Х3,Х4,Х5, Х6).

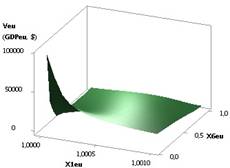
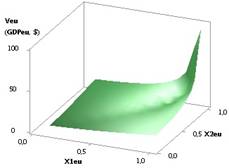
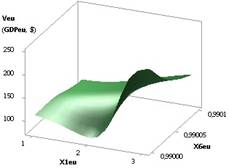
На первом рис. 1 показана зависимость GDPeu при Х1 = Х2 = Х3 = 1, Х5 = 1…0,1, Х4 = 0,99, Х6 = 0,99...0,1. Из данного рисунка видно, что значения ВВП (GDP) увеличиваются с 95,27 до 95266, т.е. в 1000 раз.

Рис. 1. ВВП (GDPeu) = f(X1, Х5) приХ1=Х2=Х3=1,Х5=1..0,1,Х4=0,99,Х6=0,99..0,1

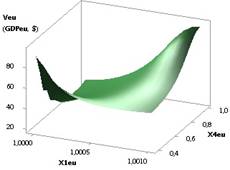
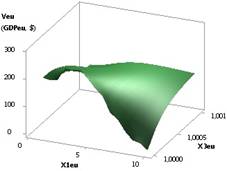
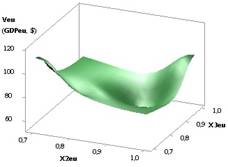
Рис. 2. ВВП (GDPeu) = f(Х1, Х4) при Х1 =Х2 = Х3 =1, Х5 =1..0,1,Х4= Х6 = 0,99..0,1

На рис. 2 представлена зависимость GDPeu, когда значения переменных Х1 = Х2 = Х3 = 1, Х5 = 1…0,1, Х4 = Х6 = 0,99...0,1. Здесь построенный трехмерный график GDPeu имеет минимум 20,67 в точке 3.

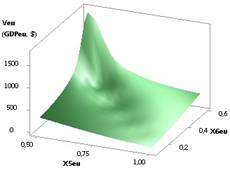
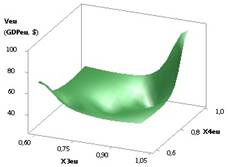
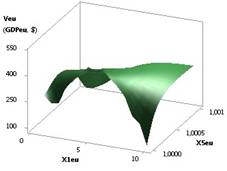
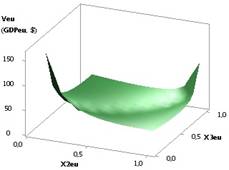
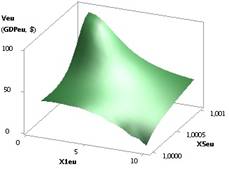
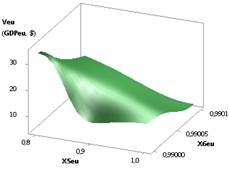
На следующих двух рисунках 3 и 4 показаны зависимости GDPeu = f(Х3, Х4) и GDPeu = f(Х2, Х3), когда переменные были Х1 = Х2 = 1,Х3 = Х5 = 1..0,1, Х4 = Х6 = 0,99...0,1 и Х1 = 1, Х2 = Х3 = Х5 = 1..0,1, Х4 = Х6= 0,99…0,1 соответственно. Значения GDPeu на рис. 3 имеет минимум 26,51 в точке 2, а потом увеличивается в 6065 раз. Зависимость GDPeu на рис. 4 также имеет минимум 14,08 в точке 4 и далее увеличивается в 11,42 раз.

Рис. 3. ВВП (GDPeu) = f(Х3, Х4) при Х1 =Х2 =1,Х3= Х5=1..0,1,Х4= Х6= 0,99..0,1

Рис. 4. ВВП (GDPeu) = f(X2, Х3) при Х1 =1,Х2 =Х3= Х5=1..0,1,Х4= Х6= 0,99…0,1

Рис. 5. ВВП (GDPeu) = f(X1, Х2) при Х1 =Х2 = Х3 = Х5 = 1..0,1, Х4 = Х6= 0,99..0,1

Рис. 6. ВВП (GDPeu) = f(Х1, Х3) при Х1 =1..10,Х2 =1..0,1, Х3= Х5=1,Х4= Х6=0,99

Рис. 7. ВВП (GDPeu) = f(Х1, Х5) при Х1 =1..10,Х2 = Х3= 1..0,1,Х5=1,Х4= Х6=0,99

Рис. 8. ВВП (GDPeu) = f(X1, Х5) при Х1 =1..10,Х2 = Х3= 1..0,1,Х5=1,Х4= 0,99..1, Х6=0,99

Следующие два рисунка 5 и 6 были построены при Х1 =Х2 = Х3 = Х5 = 1…0,1, Х4 = Х6 = 0,99...0,1 и Х1 = 1..10, Х2 = 1..0,1, Х3 = Х5 = 1,Х4 = Х6 = 0,99. Из рис. 5 видно, что здесь GDPeu уменьшается в 17 раз. На рис. 6 параметр GDPeu имеет максимум 261,41 в точке 4.

Для построения двух 3D графиков на рис. 7 и 8 были использованы следующие значениях переменных Х1 = 1...10, Х2 = Х3 = 1…0,1, Х5 = 1, Х4 = Х6 = 0,99 и Х1 = 1...10, Х2 = Х3 = 1..0,1, Х5 = 1, Х4 = 0,99…1, Х6 = 0,99. Так, например, из таблицы, на основе которой был построен рис. 7 видно, что получилась симметричная зависимость GDPeu с максимумами 495,02 в точках 5 и 6. Из рис. 8 видно, что 3D график уменьшается с 95,27 до 5,08.

Построенная зависимость GDPeu на рис. 9 при Х1 = 1...10, Х2 = Х3 = Х5 = 1...0,1, Х4 = 0,99...1, Х6 = 0,99 имеет минимум 80,18 в точке 2.

3D график GDPeu, изображенный на рис. 10 имеет минимум 54,66 в точке 2 после чего резко увеличивается в 93 раза.

Рис. 9. ВВП (GDPeu) = f(X1, Х6) при Х1 =1..10,Х2 = Х3= Х5=1..0,1, Х4= 0,99..1, Х6=0,99

Рис. 10. ВВП (GDPeu) = f(Х2, Х3) при Х1 =1..10,Х2 = Х3= Х5=1..0,1,Х4=Х6=0,99..1

Рис. 11. ВВП (GDPeu) = f(X5, Х6) при Х1 =Х2 = Х3 = 1, Х5 = 1..0,1, Х4 = 0,99, Х6= 0,1…0,99

Рис. 12. ВВП (GDPeu) = f(Х5, Х6) при Х1 =Х2 = Х3 = 1, Х5 = 1..0,1, Х4 = 0,1…0,99, Х6 = 0,99

На последних двух рисунках 11 и 12 были построены две трехмерные поверхности GDPeu при Х1 =Х2 = Х3 = 1, Х5 = 1…0,1, Х4 = 0,99, Х6 = 0,1…0,99 и Х1 = Х2 = Х3 = 1, Х5 = 1...0,1, Х4 = 0,1…0,99, Х6 = 0,99 соответственно. На рис. 11 зависимость GDPeu увеличивается с 3495 до 1738, т.е. почти в 50 раз, а на рис. 12 увеличивается с 5,08 до 32,93, т.е. в 6,67 раз.