ПРЕДСТАВЛЕНИЕ 3D ГРАФИКОВ ПРИ ШЕСТИ ПЕРЕМЕННЫХ

Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

В этой статье рассмотрены варианты влияния шести переменных на ВВП (GDP) и их изображение в трехмерном пространстве. Эти рисунки позволяют представить влияние различных переменных на ВВП (GDP). Таким образом, в статье рассмотрена зависимость изменения ВВП (GDPeu) = f(Х1,Х2, Х3,Х4,Х5,Х6).

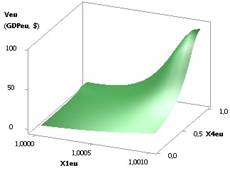
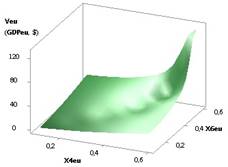
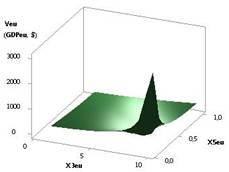
На рис. 1 показана зависимость GDPeu при Х1 = Х2 = Х5 = 1, Х3 = 1...10, Х4 = 0,99...0,1, Х6 = 0,99. Из рисунка видно, что значения ВВП (GDPeu) уменьшается с 95,27 до 0,016, т.е. в 592,45 раз.

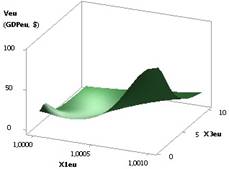
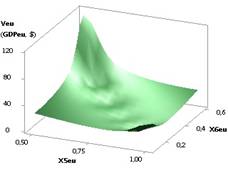
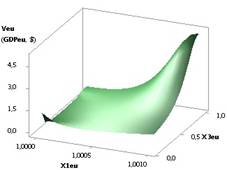
Рис. 1. ВВП (GDPeu) = f(X1, Х4) при Х1=Х2=Х5=1,Х3=1..10,Х4=0,99..0,1,Х6=0,99	Рис. 2. ВВП (GDPeu) = f(X1, Х3) при Х1= Х5=1, Х2=1..0,1, Х3=1..10,Х4= Х6=0,99
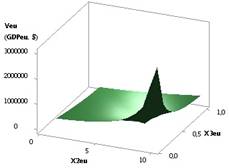
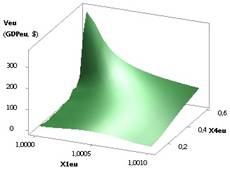
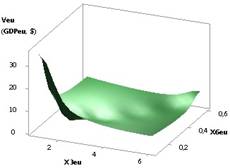
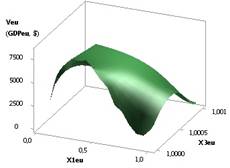
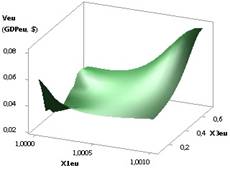
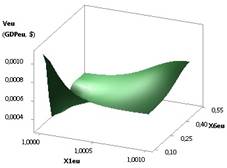
Рис. 3. ВВП (GDPeu) = f(X2, Х5) приХ1=Х5=1,Х2=1..10,Х3 = 1..0,1,Х4 = Х6 = 0,99	Рис. 4. ВВП (GDPeu) = f(X1, Х3) при Х1=1..0,1,Х2=1..10, Х3=Х5= 1, Х4= Х6=0,99

Рисунок 2 дает представление, как при увеличении одной переменной Х3 в 10 раз и уменьшении Х2, значения экономической оболочки уменьшаются в 31622,78 раз. Здесь построенная область имела следующие переменные Х1 = Х5 = 1, Х2 = 1...0,1, Х3 = 1...10, Х4 = Х6 = 0,99.

Следующие два рисунка 3 и 4 показывают две области 3D GDPeu, где на рис. 3 параметры GDPeu увеличиваются значительно до 3,01E+06, а на рис. 4 имеется максимум 8266,58 в точке 7. Эти рисунки были построены при Х1 = Х5 = 1, Х2 = 1…10, Х3 = 1...0,1, Х4 = Х6 = 0,99 и Х1 = 1...0,1, Х2 = 1...10, Х3 = Х5 = 1, Х4 = Х6 = 0,99 соответственно.

Рис. 5. ВВП (GDPeu) = f(X4, Х6) при Х1=Х2=Х3 = 1,Х5 =1..0,1,Х4 = Х6 =0,1…0,99		Рис. 6. ВВП (GDPeu) = f(X5, Х6) при Х1 =Х2 =Х3=1,Х5 =1..0,1, Х4= 0,99…0,1, Х6 = 0,1…0,99
Рис. 7. ВВП (GDPeu) = f(X1, Х4) при Х1=Х2=1, Х3=Х5=1..0,1, Х4= Х6=0,1…0,99	Рис. 8. ВВП (GDPeu) = f(X1, Х3) при Х1=Х2=1, Х3=1..0,1, Х5=1..10, Х4= 0,99…0,1, Х6=0,1…0,99

Следующие два рисунка 5 и 6 были построены при Х1 = Х2 = Х3 = 1, Х5 = 1...0,1, Х4 = Х6 = 0,1…0,99 и Х1 = Х2 = Х3 = 1, Х5 = 1...0,1, Х4 = 0,99…0,1, Х6 = 0,1…0,99. Здесь видно, что построенные 3D области GDPeu на рис. 5 увеличиваются с 1,87 до 127,63, т.е. в 68,43 раз, а на рис. 6 уменьшаются с 95,27 до 0,002, т.е. в 51443 раза.

Из рис. 7 видно, что параметров GDPeu на рис. 7 и 8 были использованы следующие значениях переменных Х1 = Х2 = 1, Х3 = Х5 = 1...0,1, Х4 = Х6 = 0,1…0,99 и Х1 = Х2 = 1, Х3 = 1...0,1, Х5 = 1...10, Х4 = 0,99…0,1, Х6 = 0,1…0,99. Из рис. 7 видно, что увеличение параметра GDPeu происходят незначительно в 193,52 раза, в то время как для рис. 8 значения GDPeu имею минимум 0,0236 в точке 8.

Область GDPeu, представленная на рис. 9 при Х1 = Х2 = 1, Х3 = 1...10, Х5 = 1...0,1, Х4 = 0,1...0,99, Х6 = 0,99...0,1, имеет минимум 2,03 в точке 3 после чего увеличивается до 3012,6. Из следующего рис. 10 видно, что построенная область GDPeu при переменных Х1 = Х2 = 1, Х3 = 1...0,1, Х5 = 1..10, Х4 = 0,1...0,99, Х6 = 0,99…0,1 имеет минимум 0,034 в точке 6 после чего увеличивается до 1,1.

Рис. 9. ВВП (GDPeu) = f(X3, Х5) при Х1=Х2=1,Х3=1..10,Х5=1..0,1,Х4=0,1...0,99, Х6 = 0,99…0,1		Рис. 10. ВВП (GDPeu) = f(X1, Х3) при Х1=Х2=1,Х3=1..0,1,Х5=1..10,Х4=0,1...0,99, Х6 = 0,99…0,1
Рис. 11. ВВП (GDPeu) = f(X3, Х6) при Х1=Х2=1, Х3=1..10,Х5 = 1..0,1, Х4 = 0,99..0,1, Х6 = 0,1..0,99	Рис. 12. ВВП (GDPeu) = f(X1, Х6) при Х1 = Х2 = 1,Х3 = Х5 = 1..10, Х4 = 0,1..0,99, Х6 = 0,99..0,1

На последних двух рисунках 11 и 12 видно, что значения построенных областей GDPeu в обоих вариантах имеют минимумы 1,42 в точке 4 (рис. 11) и 0,00031 в точке 9 (рис. 12). Эти рисунки были построены, когда значения переменных были следующими: Х1 = Х2 = 1, Х3 = 1..10, Х5 = 1..0,1, Х4 = 0,99...0,1, Х6 = 0,1...0,99 и Х1 = Х2 = 1,Х3 = Х5 = 1…10, Х4 = 0,1..0,99, Х6 = 0,99...0,1.