Òåõíè÷åñêèå íàóêè/ 12.Àâòîìàòèçèðîâàííûå ñèñòåìû óïðàâëåíèÿ
íà ïðîèçâîäñòâå.
Student Kryvopyshyn T. M., Candidate of Engineering Sciences Ladieva L. R.
National Technical
University of Ukraine “Kiev Polytechnic Institute”, Ukraine
Optimal robust control system of a reactor
synthesis to form urea melt
The synthesis process
of urea involves the stages of synthesis and dehydration of urea ammonium.
Ammonia is compressed by the compressor and through the refrigerator at a
temperature of 25 0Ñ
enters the reactor.
There is carbon monoxide (IV) with a temperature of 35 0Ñ, compressed by the compressor. Given that the process
involves recycling, one of the basic reagent is a carbamate ammonium (NH4)2CO2 which enters the reactor after the decomposition of a 75% solution of urea. Since this synthesis
reactor type "ideal mixing", all the reactants are mixed throughout
its volume, and using the heating jacket pressure reached to 2
ÌÏà, and the temperature of 170…190
0Ñ. The resulting floating
output contains 34-35 % urea,
18-19 % ammonium carbamate, 34-35 % ammonia and 10-11 % water. The flow temperature is – 175 0Ñ.
The resulting
solution of the carbamate recirculates in the reactor. The ratio of NH3 : CO2 = 3-5 : 1 . At the first stage distillation at a pressure of 1,4
ÌÏà
and temperature of 390 0Ñ output becomes to 84 % of
excess ammonia.
In the process of creating urea melt one of the most
important technological parameters on which depends the quality of the produced
raw material is the temperature of the urea melt at the exit of the reactor.
Therefore, the main channel of the regulation: "the consumption of ammonia
- temperature urea melt".
The
dynamical equation of heat balance of the reactor:
![]()
![]()
where Q – volume flow, m3/s; Ñ – the
heat capacity of a substance, J/(kg∙Ê); Òw– the temperature of the casing wall, Ê; Ò – the temperature of the substance, Ê; ñ – the density of the substance, kg/ m3; V – the volume of the reactor, m3; q – thermal effect of reaction, J/mol; Ê – the
reaction rate, mol/(m3∙s); αT – the heat transfer coefficient, J/(m2∙s∙Ê); F – the surface heat transfer, m2.
The dynamical equation of thermal balance of
heating the shell:
![]()
where αT1 – the heat transfer
coefficient between the casing wall and environment, J/(m2∙s∙Ê);
Òe – the temperature of the environment, Ê; m – the hull weight, kg; Ñ – the
heat capacity of the wall material, J/(kg∙Ê).
Highlight here two thermal capacity afloat urea and heating wall:
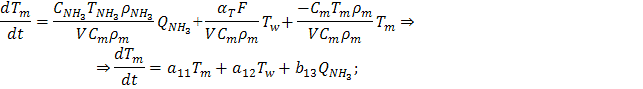
![]()
Hence the matrix status and control acquires the form:
![]()
But, there are certain parametric uncertainty is the
action of the catalyst in the reactor changes with time, and therefore, the
thermal effect is unpredictable. As a result, have a nominal mathematical model
and mathematical model with perturbations. The question arises whether the system
is robust stable?
To verify that the system is robust stable on the
Kharitonov theorem it is necessary that the interval characteristic polynomial was of the type Hurwitz, as well as
necessary and sufficient what its four angled versions was of the type Hurwitz
are of the form:
![]()
![]()
The synthesized optimal linear regulator and the
calculated gain:
![]()
where
P(t) – matrix Riccati coefficients, R – weighting factor.
This control object with an interval matrix ΔÀ=À0+À, for which the
controller implements a control law![]() so that the matrix of
the system state has the form:
so that the matrix of
the system state has the form:
![]() .
.
This control system is of order n=2 with characteristic
frequency ω0=4ñ-1 set in probeam basis and the matrix F0 becomes:
![]()
Interval part ![]() matrix condition has the form:
matrix condition has the form:
![]()
The
matrix F then there is an interval of
the characteristic polynomial:
![]()
Tested the stability of the system showed that
the system is robust stable, all the Kharitonov polynomials were of the type Hurwitz.
Optimal control with a given quality criterion
for such a law regulation:
![]() ,
,
having a linear matrix inequality:
![]()
Multiplying this expression to the left and to
the right on Q=P-1, we
obtain:
![]()
The criterion value is determined when the choice of a
stabilizing control. To this end, we introduce the parameter γ >0:
![]()
If for a given γ >0 will be his decision Q, having feedback:
![]()
the value of the functional is:
![]()
The parameter γ plays the role of a parameter is
its optimal value corresponds to the minimum of the functional J.
|
|
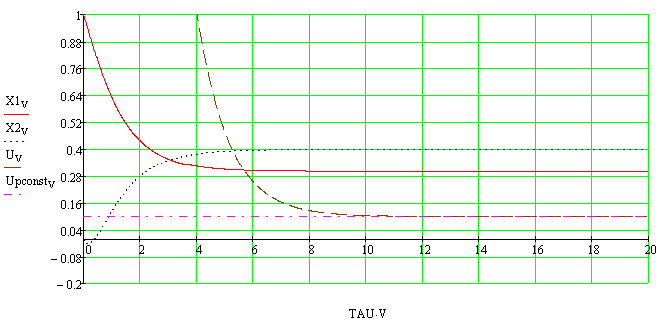
Pic.1. Schedule changes of the state variables
and the control vector
X1v, X2v – state
variables; Uv – the control vector; Upconstv – set the control vector
Was calculated parametric uncertainty is the action of
the catalyst was set to 30 % and was calculated its effect on the
circuit.
Literature:
1. Ëà䳺âà Ë. Ð. Îïòèìàëüíå êåðóâàííÿ ñèñòåìàìè.: Íàâ÷. ïîñ³á. –
Ê.: ÍÌÖ ÂÎ, 2000 – 187ñ.
: ³ë. – Á³áë³îãð.: ñ. 185–186. – 200 ïð. –
ISBN 966-622-026-1.
2. Gahinet P., Aprakian P. Linear Matrix Inequality Approach to H∞
control // Int. J. Robust and Nonlinear Contr. 4. – 1994. – P.421
– 448.
2. Ïîëÿê Á. Ò., Ùåðáàêîâ Ï. Ñ. Ðîáàñòíàÿ óñòîé÷èâîñòü è
óïðàâëåíèå. –Ì.: Íàóêà, 2002 . – 303 ñ. –
ISBN 5-02-002561-5.
3. Áðàéíåñ
ß. Ì. Ââåäåíèå â òåîðèþ è ðàñ÷åòû õèìè÷åñêèõ è íåôòåõèìè÷åñêèõ ðåàêòîðîâ / ß.
Ì. Áðàéíåñ. – 2-å èçä., ïåðåðàá. è
äîï. – M. : Èçä-âî
"Õèìèÿ", 1976. – 232 ñ. :
èë., òàáë. ; 22 ñì. – (Ïðîöåññû è
àïïàðàòû õèìè÷åñêîé è íåôòåõèìè÷åñêîé òåõíîëîãèè). – Áèáëèîãð.: ñ. 224–226.
4.
Íèêèôîðîâ Â. Î., Ñëèòà Î. Â., Óøàêîâ À. Â. Èíòåëëåêòóàëüíîå óïðàâëåíèå â óñëîâèÿõ
íåîïðåäåëåííîñòè: ó÷åáíîå ïîñîáèå. – ÑÏá.: ÑÏáÃÓ ÈÒÌÎ, 2011 ã. – 226 ñ. : èë. 33.