Современные информационные технологии/Вычислительная техника и программирование

Пилипчук А.О., Мясіщев О.А.

Хмельницький національний університет, Україна

Оцінка швидкодії технології CUDA для вирішення систем лінійних рівнянь

На сьогоднішній день обчислення лінійних рівнянь у науці широко використовується. Основна проблема – це швидкодія їх вирішення. Розроблено багато методів, які певним чином спрощують цю задачу. Більшість методів основані на представленні матриці у вигляді множення двох матриць певного вигляду або матричних розкладах (факторизаціях). Як правило, після розкладу матриці задача рішення системи лінійних рівнянь значно спрощується. Розглянемо систему Ax=b. Тоді LU-розкладом буде називатись розклад вигляду LUx=b, де Ux=y, а Ly=b. При цьому LU=A. Матриця U – верхня трикутна матриця, а матриця L – нижня трикутна матриця. Цей метод оснований на методі Гауса, але на відміну від нього вектор b не використовується.

Використаємо наступні позначення для елементів матриці: L= L ij, U= U ij, i, j = 1 … n; Діагональні елементи матриці L -  lij =1, i, j = 1 … n. Для знаходження матриць L та U використаємо формули:

1.         U1j = А1j,  i = 1 … n

2.         L ij = ,  j = 2 … n (U1j ≠ 0)

Для i= 2 … n

1.         Uіj = Аіj - 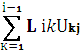 ,  j = i … n

2.         Ljі ==   (  Аjі - 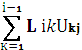) ,  j = i+1 … n

В результаті отримуємо матриці L та U. В програмній реалізації даного методу для компактного представлення матриць L та U використовують всього один масив, в якому об’єднують ці матриці. Наприклад матриця розміром 3х3.

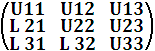
В результаті отримуємо таку рівність як А=LU. Такий розклад Матриці А має значну перевагу перед методом Гауса. Адже при цьому взагалі не згадується про праву частину рівняння. Тобто зовсім не використовується вектор b для LU-розкладу. Тому можна значно спростити задачу вирішення систем лінійних рівнянь. Початкова система набуває вигляду LUx=b. Його розв’язання тепер рівносильне послідовному розв’язку систем рівнянь Ly=b, Ux=y, з трикутними матрицями, звідки й знаходять шуканий вектор х. Розкладання А=LU відповідає прямому ходу методу Гауса, а розв’язання систем рівнянь Ly=b, Ux=y – зворотному ходу.

Але знайти LU-розклад для певної квадратної матриці А вдається не завжди, адже в процесі обрахунку ведучі елементи можуть приймати значення 0 або близькі до нього значення. Тому в прикладних задачах використовують LUP-розклад. Якщо матриця не вироджена, то для неї можна розрахувати LUP-розклад PA=LU. Нехай PA=B. B-1 =D. Тоді через властивості оберненої матриці можна записати D=U-1L-1. Якщо помножити ці рівності на L та U, то можна отримати дві рівності вигляду UD= L-1 DL= U-1. Перше з них представляє собою систему з n2 лінійних рівнянь для  із яких відомі праві частини (із властивостей трикутних матриць). Друге також представляє собою систему з n2 лінійних рівнянь для  із яких відомі праві частини (із властивостей трикутних матриць). Разом вони представляють собою систему з n2 рівнянь елементів матриці D. Тоді з рівняння (PA) -1=A-1P-1=B-1=D, тоді отримуємо A-1=DP. Цей алгоритм приведення систем рівнянь до системи з верхньою трикутною формою ефективно реалізується на паралельних процесорах.

Наприклад, паралельне вирішення цієї задачі можливе на графічному процесорі. Існують спеціальні бібліотеки для вирішення типових задач на NVidia CUDA. Одна з них MAGMA (Matrix Algebra on GPU and Multicore Architectures). Для LUP-розкладу потрібно використати функцію magma_sgetrf_gpu. Для знаходження вектору х використовується функція magma_sgetrs_gpu. Для полегшення написання коду ці функції об’єднали у функцію  magma_sgesv_gpu.

Програма вирішення задачі rf_rs_cpugpu.cpp на СPU і GPU:

#include <math.h>

#include <cuda.h>

#include <cuda_runtime_api.h>

#include <cublas.h>

#include "flops.h"

#include "magma.h"

#include "magma_lapack.h"

#include "testings.h"

#define PRECISION_s

#if defined(PRECISION_z) || defined(PRECISION_c)

#define FLOPS(m, n) ( 6. * FMULS_GETRF(m, n) + 2. * FADDS_GETRF(m, n) )

#else

#define FLOPS(m, n) (      FMULS_GETRF(m, n) +      FADDS_GETRF(m, n) )

#endif

int main( int argc, char** argv)

{TESTING_CUDA_INIT();

magma_timestr_t  start, end;

float flops, gpu_perf, cpu_perf, error, *h_A, *h_R, *h_B, *h_LU,*h_X, *d_A;

magma_int_t M = 0, N = 0, n2,szeB, lda,ldb, ldda, NRHS=1, *ipiv;

magma_int_t size[10] = {960,1920,3072,4032,4992,5952,7104,8064,9024,9984};

magma_int_t i, info, min_mn, nb, maxn, ret, ione = 1, ISEED[4] = {0,0,0,1};

if (argc != 1){ for(i = 1; i<argc; i++){ if (strcmp("-N", argv[i])==0)

N = atoi(argv[++i]);

else if (strcmp("-M", argv[i])==0) M = atoi(argv[++i]);}

if (M>0 && N>0) printf("  testing_sgetrf -M %d -N %d\n\n", M, N);

else { printf("\nUsage: \n"); printf("  testing_sgetrf -M %d -N %d\n\n", 1024, 1024);

exit(1);}}

else {printf("\nUsage: \n");printf("testing_sgetrf_gpu -M %d -N %d\n\n", 1024, 1024);

M = N = size[9];}

ldda   = ((M+31)/32)*32; maxn = ((N+31)/32)*32; n2 = M * N; min_mn = min(M, N);

nb     = magma_get_sgetrf_nb(min_mn);

TESTING_MALLOC(ipiv, magma_int_t, min_mn);

TESTING_MALLOC(h_A, float, n2); TESTING_HOSTALLOC( h_R, float, n2     );

TESTING_DEVALLOC(d_A,float,ldda*N);

TESTING_MALLOC(h_B,float,N*NRHS);TESTING_MALLOC( h_LU, float, n2 );

TESTING_MALLOC( h_X,  float, N*NRHS );

printf("\n\n"); printf("  M     N   CPU GFlop/s    GPU GFlop/s);

printf("=================================================\n");

for(i=0; i<10; i++){ if (argc == 1){ M = N = size[i];}

min_mn= min(M, N); lda = ldb  = M; n2    = lda*N; szeB = ldb*NRHS;

ldda  = ((M+31)/32)*32; flops = FLOPS( (float)M, (float)N ) / 1000000;

lapackf77_slarnv( &ione, ISEED, &n2, h_A );

lapackf77_slarnv( &ione, ISEED, &szeB, h_B );

lapackf77_slacpy( "F", &N, &N,    h_A, &lda, h_LU, &lda );

lapackf77_slacpy( "F", &N, &NRHS, h_B, &ldb, h_X,  &ldb );

lapackf77_slacpy( MagmaUpperLowerStr, &M, &N, h_A, &lda, h_R, &lda );

start = get_current_time();

lapackf77_sgetrf(&M, &N, h_A, &lda, ipiv, &info);

lapackf77_sgetrs(MagmaNoTransStr,&N,&NRHS,h_A,&lda,ipiv, h_B, &ldb, &info );

end = get_current_time();

if (info < 0) printf("Argument %d of sgetrf had an illegal value.\n", -info);

cpu_perf = flops / GetTimerValue(start, end);

cublasSetMatrix( M, N, sizeof(float), h_R, lda, d_A, ldda);

start = get_current_time();

magma_sgesv( N, NRHS, h_LU, lda, ipiv, h_X, ldb, &info );

end = get_current_time();

if (info < 0) printf("Argument %d of sgetrf had an illegal value.\n", -info);

if (ret!=MAGMA_SUCCESS) printf("sgetrf_gpu returned with error code %d\n", ret);

gpu_perf = flops / GetTimerValue(start, end);

printf("%5d %5d  %6.2f         %6.2f\n", M, N, cpu_perf, gpu_perf);

if (argc != 1) break; }

TESTING_FREE( ipiv ); TESTING_FREE( h_A ); TESTING_HOSTFREE( h_R );

TESTING_DEVFREE( d_A ); TESTING_CUDA_FINALIZE(); }

Дослід проводився на одному ядрі CPU AMD PhenomII X4 955, 3200MHz та GPU GeForce GTX460, 1350MHz, 1023.2MB. Використовувалась 32-х розрадна операційна система Linux Ubuntu 10.04 з компілятором gcc.

В таблиці 1 представлені результати швидкодії на CPU та GPU, дані в Gflops/s.

Таблиця 1. Результати обчислення LU-розкладу на CPU та GPU.

Розмірність матриці

Розклад та розв’язок (rf_rs_cpugpu.cpp)

Розклад

(тестова програма)

Розклад та розв’язок

(rf_rs_cpugpu.cpp)

Розклад

(тестова програма)

З бібліотекою ATLAS

Без бібліотеки ATLAS

CPU

GPU

CPU

GPU

CPU

GPU

CPU

GPU

960х960

5.76

21.86

8.07

27.25

1.94

18.47

1.95

21.73

1920х1920

10.31

55.72

10.47

72.81

2.01

45.05

2.02

54.09

3072х3072

10.91

63.58

11.01

73.72

1.98

49.47

1.99

55.13

4032х4032

12.61

106.48

12.70

132.19

1.89

64.54

1.89

71.95

4992х4992

13.14

131.74

13.22

162.99

1.98

82.05

1.99

91.66

5952х5952

13.52

159.60

13.58

197.71

1.88

96.69

1.89

107.63

7104х7104

13.91

189.44

13.96

234.57

1.88

115.90

1.89

128.99

8064х8064

14.12

207.89

14.17

255.94

1.98

134.16

1.99

149.92

9024x9024

14.31

226.97

14.34

277.57

1.88

147.67

1.88

164.35

9984x9984

14.42

239.43

14.46

289.07

1.97

165.90

1.98

185.61

Висновки

1.Основна трудомісткість LU-розкладу припадає на сам розклад. Розв’язок системи на основі вже побудованих трикутних матриць займає досить мало ресурсів як центрального так і графічного процесора.

2.Без використання бібліотеки ATLAS, при великих розмірах матриць отримаємо прискорення на GPU відносно CPU у 80-90 разів, з ATLAS у 16 - 19 разів. При використанні ATLAS швидкодія GPU збільшиться у 1.3 -1.5 рази, CPU у 7 – 7,3 рази.

3.Якщо теоретично використати 4 ядра процесора, його сумарна продуктивність процесора на маленьких розмірах матриці зрівнюється з GPU при використанні ATLAS. При розмірах матриці біля 10000 ел. GPU швидше CPU приблизно у 5,5 рази.

Література.

1.                     MAGMA Documentation: http://icl.cs.utk.edu/magma/docs/

2.                     LU Matrix Decomposition in parallel with CUDA: http://www.noctua-blog.com/index.php/2011/04/21/lu-matrix-decomposition-in-parallel-with-cuda/