Математика/4. Прикладная математика

Кушумбаева З.А.

Университет Манчестера, Великобритания

О конечно-разностном методе Эйлера и его программной реализации

Дифференциальные уравнения, которые возникают при решении вариационных задач, редко удается проинтегрировать. В связи с этим возникает потребность приближенных методов решения этих задач. Методы приближенного решения вариационных задач называют прямыми методами. Основная идея прямых методов заключается в том, что вариационная задача рассматривается как предельная для некоторой задачи на экстремум функции конечного числа переменных [1]. Эта задача на экстремум функции конечного числа переменных решается обычными методами, а затем предельным переходом получается решение соответствующей вариационной задачи. Очень хорошо изложен материал по этим методам в [1].

Рассмотрим конечно - разностный метод Эйлера.

Пусть дана простейшая вариационная задача: найти экстремум функционала

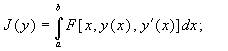у(а)=А, у(b)=B. (1)

В методе Эйлера значения функционала (1) рассматриваются не на произвольных, допустимых в данной вариационной задаче кривых, а лишь на ломанных, составленных из заданного числа прямолинейных звеньев, с заданными абсциссами вершин

где

На этих ломанных функционал превращается в функцию ординат вершин ломанной. Ординаты выбираются так, чтобы функция достигала экстремума, т.е. они определяются из системы уравнений

, , … , . (2)

Полученная ломаная является приближенным решением вариационной задачи (1) (см. рис. 1).

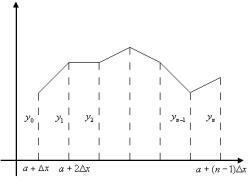
Рисунок 1. Ломаная Эйлера.

Рассмотренный метод приближенного решения вариационных, с помощью ломанных Эйлера представляет собой алгоритм численного решения вариационной задачи с достаточно сложной системой уравнений. Особенно трудоемки вычисления при большом числе звеньев ломанной. Для решения данной проблемы, была поставлена задача, реализовать данный метод на ЭВМ, чтобы все громоздкие вычисления выполняла машина.

В качестве примера приведем вычисление функционала:

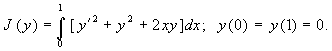
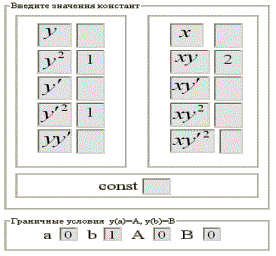
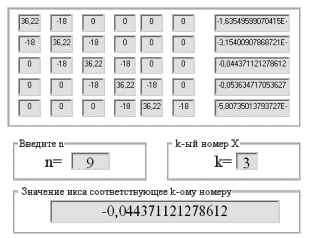
Решение данного функционала при будет выглядеть следующим образом.

Решив данную задачу точным методом в Mathcad, получим следующее значение:

_.

Точное решение	Приближенное решение
-0,4444121	-0,44371121278612

Программа проста и удобна для пользователя и позволяет находить значения при достаточно больших п, без громоздких вычислений вручную.

Литература:

1. Краснов М.Л., Киселев А.И., Макаренко Г.И. Вариационное исчисление. – М.: высш. шк., 2003. с. 241.