педагогические науки

к.п.н. Р.А. Ганиева

Балтийская государственная академия Рыбопромыслового флота

Знаковая модель курса высшей математики

для студентов специальностей технического профиля

(на примере темы «Кратные интегралы»)

 

         Нередко  студенты сетуют на то, что изложенная информация  не откладывается у них  в памяти и им  не удается понять или запомнить учебный материал. Время от времени подобное случается с каждым из нас.  Как же можно усилить способность понимать? Необходима стратегия, способствующая сделать субъективно новую информацию  более доступной к пониманию, сохранению и последующему ее воспроизведению.

Понимание и распознавание информации у человека происходит через схемы, объединяющие формальные категории в группу или кластер по функциональному признаку. Больший объем информации мы получаем через зрительный канал. Поэтому в качестве стратегии, способствующей пониманию и усвоению учебной информации по высшей математике, нами была принята разработка знаковой модели курса высшей математики.

Под знаковой моделью курса высшей математики понимается совокупность  тематических модулей. Тематический модуль - это  набор разработанных по определенным правилам  схем изучаемых в данной теме математических понятий. В основу алгоритма построения знаковой модели курса высшей математики для студентов нематематических специальностей были положены подходы: системно-логический, когнитивный, конструктивный.

         Системно-логический подход основан на методе содержательно-генетической логики и принципах системного подхода. Изучением особых объектов: знаний, процессов решения задач занимается содержательно - генетичес-кая  логика. В соответствии с методами содержательно - генетической логики результаты  исследования  могут быть представлены  только в структурных или блочных схемах.  Выделяют как минимум два разных употребления одной и той же схемы: 1) как строения некоторого объекта;  2) для изображения функционирования или изменения объекта. Для моделирования объекта требуется выделить такие схемы и развернуть их по некоторым правилам. При разработке знаковой модели курса высшей математики мы использовали схемы первого функционального назначения(2). В качестве объектов моделирования выступают математические понятия, изучаемые в каждом разделе курса высшей математики.

С позиций системного подхода, основополагающего методологического метода, каждое математическое понятие следует рассматривать как систему, построенную  в соответствии с принципами системного подхода целостности, структурности , иерархичности и предназначенную для передачи учебной математической информации. Структурность предполагает не только детерминацию элементов системы, но и установление связей и отношений функционально-значимых элементов. Иерархичность  означает, что каждый элемент системы в свою очередь можно рассматривать также как систему(3).

         В математике наряду с основополагающим формально-логическим методом применяется также конструктивный подход. Согласно данному подходу математический факт считается установленным, если получена соответствующая конструкция: формульная, графическая или в виде таблицы, рисунка. Очевидно, что конструктивизм в большей степени опирается на зрительный образ. Это повышает эффективность восприятия и усвоения субъективно новых знаний и является большим преимуществом конструктивного метода по отношению к  формально-логическому.

Опора  конструктивного метода в математике на зрительный образ не случайна и обусловлена  особенностями  психологических механизмов  организации познавательных процессов человека. Одно из пониманий когнитивной психологии – это понимание ее как науки о процессах приобретения, хранения, преобразования, порождения и применения человеком знаний, то есть как науки о познании.  При организации процесса познания необходимо учитывать психологические механизмы и функции  познавательных процессов. Поэтому подход к разработке структурно-логических схем математических понятий с учетом психологических особенностей  восприятия, внимания, памяти, мышления мы определили как когнитивный подход. На основе анализа научного знания в области познания и познавательных процессов  были выведены наиболее значимые с нашей точки зрения их психологические особенности и механизмы, которые можно и были учтены при разработке знаковой модели курса высшей математики.

Сенсорные процессы, конкретнее зрительное восприятие, влияет на правильность ответа. В свою очередь на эффективность решения задач с привлечением сенсорных процессов влияет направленность внимания, важнейшей функцией которого  избирательность или селективность.  При  этом объем внимания ограничен , 7-9 объектов для взрослого человека.  Память   позволяет человеку фиксировать факт взаимодействия с  информацией, сохранять этот результат в форме опыта и использовать его в своей деятельности.  Для студентов вузов специальностей технического профиля особенно важно припомнить актуально значимую математическую информацию, так как изучается высшая математика на младших курсах и востребованность многих  математических знаний отсрочена. На результативность и стратегию запоминания влияет объем, степень и последовательность репрезентации учебной информации. В основе организации памяти человека лежат ассоциации. Что касается мышления, то неразрывна с этим познавательным процессом речь как форма проявления языка человека. Виновником же неспособности человека понять ту или иную информацию часто бывает даже несложность самой информации, а язык ее изложения. Математический язык, с одной стороны, универсальный язык науки. С другой, формальный язык, и именно с этим связаны трудности у студентов в  восприятии математической информации (2,7,8).

         C целью  интерпретации  каждого математического понятия, как системы, был  проведен анализ логики изложения математической информации и  выявлен ассоциативный ряд, отражающий обобщенную  структуру  абстрактного математического понятия.  Структура  конкретного математического понятия реализуется  определенным набором  единиц из  этого ассоциативного ряда, включающего в себя:   «определение»,  «обозначение», «условие существования», «виды», «действия»  («операции»), «способы вычисления» («методы нахождения», «формула нахождения, вычисления»),  «свойства» (либо самого понятия, либо действий или операций над ним), «геометрический смысл» («геометрическая интерпретация», «графическое 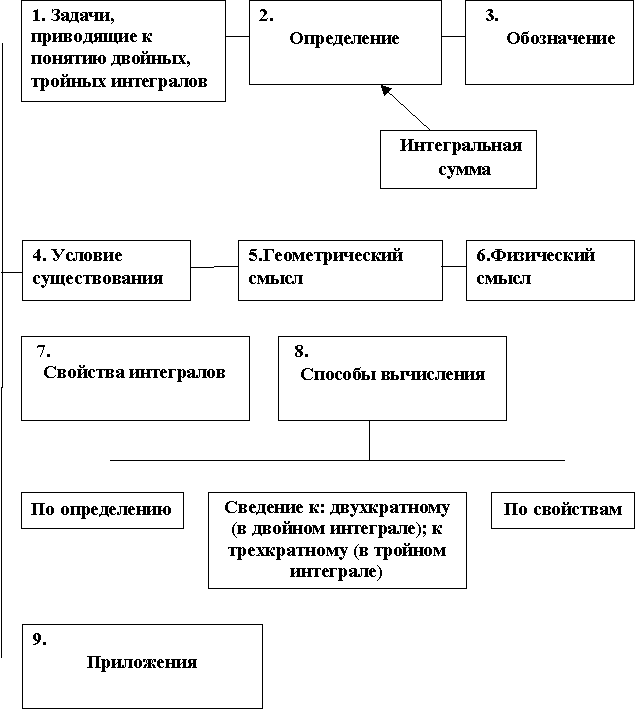изображение»), «физический смысл»,   «приложения».  В качестве примера представлена структура кратных интегралов (рис. 1).

 Иерархичность проявляется в том, что некоторые логические единицы в свою очередь также имеют свою структуру, то есть представляют собой систему(3). Между понятиями существуют различные связи. Эти связи позволяют установить ассоциации между понятиями, что способствует целостному восприятию и усвоению отдельных математических понятий, тем , разделов и курса высшей математики. В схемах мы отразили только связи по принципу «комплетивности». Комплетивность  от латинского completus – полный. Комплетивные отношения – это отношения, при которых зависимый компонент словосочетания является необходимым смысловым дополнением (5). Применительно к математике можно сказать одно понятие дополняет или раскрывает содержание другого. Так,  с  кратными интегралами  комплетивным отношением связана интегральная сумма, что отмечено особо в структурно-логической схеме данных понятий, входящей   стрелкой (рис.1). Интегральная сумма также имеет свою структуру, то есть представляет собой систему.

         Реализация  конструктивного и когнитивного подходов  заключается в форме презентации структурированной учебной  математической информации.

 Тематические модули представлены  посредством зрительных образов ( графов, рисунков, таблиц).  Учитывая ограниченность объема внимания и особенностей организации мнемической системы человека, объем информации на листе ограничен,  расположение и презентация зависит от  ее значимости в контексте модуля, содержание каждого  зрительного образа (структурной  единицы, таблицы, рисунка) минимально и представлено в знаково-символьной форме. Причем математический язык используется в сочетании с естественным языком.

         Таким образом, знаковая модель курса высшей математики - система структурно-логических схем, развернутых по общим правилам, и представленных  в соответствии с определенными требованиями. Фрагмент знаковой модели курса высшей математики представлен на рисунках 1,2. Такая знаковая модель обладает достаточно широкими дидактическими и развивающими ресурсами, что подтверждено многолетним  опытом ее внедрения в реальную практику обучения.    

Литература:

1. Баврин И.И. Высшая математика: Учеб. для студ. естественнонаучных специальностей педагогических вузов / И.И.Баврин. - 4-е изд., испр. и доп. – М.: Издательский центр «Академия», 2004. – 616с.

2.Когнитивная психология. Учебник для вузов/ Под ред. В.Н. Дружинина, Д.В.Ушакова.-М.:ПЕР СЭ,2002.-480с.

3.Новая философская энциклопедия,т.3. М: Мысль,2001.  С.553

4.Письменный Д.Т.Конспект лекций по высшей математике: полный курс /Д.Т.Письменный.-4-е изд.-М.:Айрис-пресс,2006.-608с.

5.Розенталь Д.Э., М.А. Теленкова  Справочник по русскому языку./Д.Э.Розенталь,М.А.Теленкова –М:ООО «Издательский дом «ОНИКС 21 век ООО «Издательство «Мир и образование», 2003, С.170

6.Розин В.М. Логико-семиотический анализ знаковых средств геометрии (к построению учебного предмета), С.202-205 // Педагогика и логика.-М:Касталь,1992.-409с.

7.Рубинштейн С.Л. Основы общей психологии./С.Л.Рубинштейн-СПб.:Питер,2002.-720с.

8.Халперн Д. Психология критического мышления –СПб: Издательство «Питер»,2000.-512с.

 

 

 

 

 

 

 

 

Структура

кратных интегралов  (двойных, тройных)

 

 

 

 

 


                                                                   

 

 

                         

 

 

 

 

 

 

 

 

 

 

                                      

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


                                                        

 

 

 

 

 

 

 


     Рисунок 1  Структура  кратных  интегралов

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Интегральной суммой

Для  функции z = f(x, y) в некоторой ограниченной и замкнутой области D называют  выражение вида:        

  (1)  

    M(ξi, ŋi)-; -площадь частичной области 

 

2.Определение: Конечный  предел интегральной суммы  (1) при условии, что  () ,  называют двойным интегралом от функции z= f(x,y) по области D  и  обозначают   

           

 
                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                        

Обозначение: f(x,y)dxdy,

dxdy = dS – элемент области;

D – область интегрирования;

f(x,y) - подинтегральная функция
 

Обозначение: f(x,y)dxdy,

dxdy = dS – элемент области;

D – область интегрирования;

f(x,y) - подинтегральная функция
 

3.Обозначение   f(x,y)dxdy,

D – область интегрирования;

f(x,y) - интегрируемая функция

в области D;

dxdy = dS – элемент площади.

 
 
                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                        

Обозначение: f(x,y)dxdy,

dxdy = dS – элемент области;

D – область интегрирования;

f(x,y) - подинтегральная функция
 

Обозначение: f(x,y)dxdy,

dxdy = dS – элемент области;

D – область интегрирования;

f(x,y) - подинтегральная функция
 
                                                                                                                                                                                                                   

 

 

 

          Рисунок  2   Содержание структурных единиц   №1,№2,№3                                                                                                                двойного интеграла