Физика/1. Теоретическая физика

А.И. Спольник, В.Г. Власенко, И.В. Волчок,
Л.М. Калиберда, М.А. Чегорян

Харьковский национальный технический университет

сельского хозяйства им. П. Василенко

Возбуждение изобар-аналоговых состояний

в реакциях квазиупругого рассеяния

В реакциях (p, n) с возбуждением уровней конечного ядра, которые являются изобарическими аналогами основного состояния ядра мишени, конечное ядро остается в возбужденном состоянии, которое, тем не менее, имеет спин и четность основного состояния. Это открывает некоторые новые возможности для исследования спиновой зависимости оптического потенциала, поскольку поляризация конечных ядер не является уже «вещью в себе», как в случае обычного упругого рассеяния, а может быть измерена определением круговой поляризации - квантов, испускаемых конечным ядром. Поэтому, представляется интересным рассмотреть, какие экспериментальные возможности открывает исследование поляризации конечных ядер с точки зрения определения параметров оптического потенциала, в частности, спин-спинового члена, который необходимо вводить для описания упругого рассеяния на конечных ядрах.

Для наших целей оптический потенциал, вводимый для описания квазиупругого рассеяния удобно выбрать в виде:

,

где оператор в фигурных скобках проектирует нf состояние с полным спином (–изотопический спин ядра мишени). Нейтронам, в соответствии с принятыми в теории изотопических эффектов соглашениями, приписывается проекция , тогда нейтронно- избыточные ядра имеют положительную проекцию изотопического спина . Для объяснения поляризации конечных ядер воспользуемся борновским приближением.

Таким образом, для нахождения амплитуды процесса нам нужно вычислить матричный элемент:

,

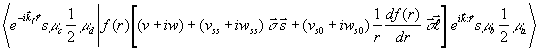где .

Все операторы, входящие в выражения можно рассматривать как тензорные операторы ранга 1, т.е. любой вектор имеет компоненты:

; .

Скалярное и векторное произведения тензорных операторов определяются следующим образом:

С использованием теоремы Вингера-Эккарта, для матричных элементов тензорных операторов получим:

=;

=

=;

=

= ,

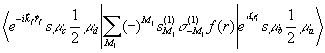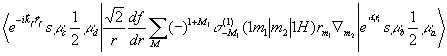где

Если воспользоваться равенством , то амплитуда процесса может быть записана

,

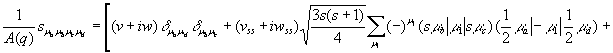
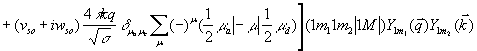где .

Мы пренебрегаем кулоновским смещением энергии ядра мишени по отношению к конечному ядру, поскольку нашей задачей является просто указание на существование эффекта, и мы вправе пренебречь обстоятельствами, имеющими второстепенный характер для настоящего расчета. В нашем приближении для поляризации конечных ядер получается следующее выражение:

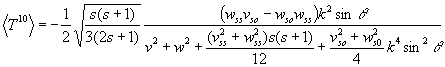
Таким образом, поляризация конечных ядер оказывается зависящей от спин-спиновой и спин-орбитальной частей потенциала. Появление в формуле связано с тем, что и не имеют размерности энергии. Величина описывает поляризацию конечных ядер в системе координат с осью , перпендикулярной плоскости реакции и осью вдоль падающего протонного пучка.