К.ф.-м.н. Липовский В.И.

Днепропетровский национальный университет, Украина

К вопросу о выборе оптимальной формы ротора

Оптимальной формой ротора, является та, которая бы обеспечивала максимум кинетической энергии вращения ротора, была прочной и жесткой. Основными факторами, оказывающими влияние на величину кинетической энергии вращения ротора, являются угловая скорость его вращения и форма ротора, определяющая момент инерции конструкции. Увеличение угловой скорости возможно в случае наиболее полного использования физико-механических свойств материала. Это возможно если в каждой точке ротора будет возникать максимально возможное напряженное состояние. Предельному напряженному состоянию соответствует наибольшее для используемого материала значение напряжения. Поскольку ротор находится в условиях сложного напряженного состояния и возникающие от центробежных сил напряжения являются положительными, тогда равнопрочная конструкция будет при значениях напряжения равных допускаемому напряжению материала. Рассмотрим различные конструкции роторов и определим влияние вида геометрии на напряженно-деформированное состояние ротора. Во всех расчетах считаем, что материал обладает изотропными однородными свойствами и работает в пределах упругих деформаций.

В качестве базовой модели формы ротора принимаем тонкий обод. Пусть свободный тонко-ободовый маховик-ротор имеет массу М, средний диаметр D и вращается с угловой скоростью . Рассмотрим полукольцо. На него будет действовать распределенная центробежная сила . Эта сила приложена в центре полукольца на расстоянии от оси вращения равном . В полукольце возникают внутренние силы, которые уравновешиваются центробежной силой, действующей на половину обода. То есть каждое волокно обода работает в условиях одноосного напряженного состояния под действием окружных напряжений. Сила инерции равна . Причем масса ротора равна (здесь - плотность материала, А - площадь поперечного сечения обода). Из-за симметрии полукольца растягивающее ротор внутренне усилие равно половине центробежной силы. Нормальное к поперечному сечению ротора напряжение определится: . Поскольку окружная скорость обода ротора в равна , , тогда допустимая линейная скорость определится из условия прочности и будет иметь предельное значение . Полученной наибольшей линейной скорости соответствует кинетическая энергия . Величина удельной энергии на единицу массы будет равна:

. (1)

Рассмотренный вариант определяет предельное значение удельной энергии для конструкций ротора в виде диска с ободом. Данное решение приведено в работе [1].

Рассмотрим вращающийся диск постоянной толщины. Геометрические характеристики следующие: внешний диаметр D=2R, толщина , в центральной зоне – отверстие диаметром . В общем случае диск может быть равномерно нагружен распределенным давлением p₀ на внутренней поверхности отверстия и распределенной нагрузкой на внешней цилиндрической поверхности p. Решение задачи о напряженно-деформированном состоянии такого диска приведено в работе [2]. Функциональные зависимости радиальных и окружных напряжений от радиуса определяются из решения системы двух дифференциальных уравнений и имеют следующий вид:

(2)

(3)

где

коэффициент Пуассона. В случае отсутствия поверхностной нагрузки на внутренней и внешней поверхности диска , то диск находится под действием только центробежных сил. Решение задачи существенно упрощается и в этом случае корректно сравнивать напряженные состояния диска постоянной толщины и диска в виде тонкого обода. Оба диска находятся в одинаковых условиях нагружения. При отсутствии нагрузки в диске постоянной толщины , а радиальные напряжения на внутренней и наружной поверхности равны нулю. Это напряжение изменяется по квадратичной зависимости, и свое наибольшее значение достигает при значении радиуса равного . Экстремум функции найден из выражения , а максимальное напряжение равно:

.

Окружное напряжение имеет наибольшее значение на внутренней поверхности отверстия при значении :

Нетрудно установить, что <,

а <. На основании первой теории прочности можно определить предельную окружную скорость диска :

(4)

Данное соотношение при значении переходит в соотношение для тонкого обода , а при очень малых отверстиях в выражение:

(5)

Рассмотрим диск постоянной толщины без отверстия, находящийся под действием центробежных сил вызванных вращением диска относительно оси симметрии. Напряжения в диске на расстоянии от центра диска определятся:

В этом случае наибольшие радиальные и окружные напряжения возникают на оси симметрии при значении и равны между собой:

(6)

Сравнивая формулы (5) и (6) можно сделать вывод, что для заданного материала конструкция ротора в виде сплошного диска является более рациональной, чем в виде диска с отверстием. Диск без отверстия достигает предельного напряженного состояния при окружной скорости, которая в примерно 1,42 раза выше окружной скорости диска с отверстием. Сравним величину удельной кинетической энергии для двух дисков одинаковой массы: диска без отверстия и с отверстием. Диск без отверстия постоянного толщины с массой M радиусом R имеет значение кинетической энергии равной . Величина удельной энергии на единицу массы равна . Из условия прочности величина удельной энергии будет равна:

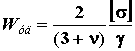(7)

Аналогично для диска с отверстием кинетическая энергия определится:

. Из условия прочности (4) величина удельной энергии:

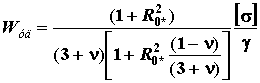. (8)

Рассмотренные примеры простейших конструкций характеризуются неоднородностью напряженно-деформированного состояния по радиусу диска. Неоднородность напряженно-деформированного состояния во вращающихся дисках исчезает в дисках равного сопротивления. В этом случае подбирается такой закон изменения ширины диска h(r) при котором выполняется равенство радиальных и окружных напряжений между собой. Принимая , из уравнения равновесия толщина диска равного сопротивления определится в виде:

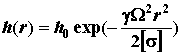. (9)

Здесь толщина диска на оси вращения диска при r=0. Толщина диска равна: 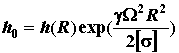, где R – габаритный радиус, h(R) – минимальная толщина диска. Определим величину кинетической энергии диска равной прочности. Масса диска переменной толщины по радиусу определится соотношением: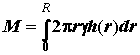. Для диска радиуса R масса равна: 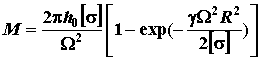. (10)

Кинетическая энергия равнопрочного ротора , где , после интегрирования определится:

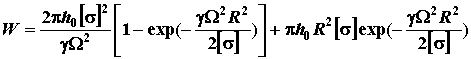. (11)

Величина удельной энергии будет равна:

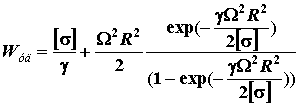. (12)

Полученные соотношения показывают, что экспоненциальный характер изменения толщины диска по радиусу приводит к увеличению габаритов конструкции. Быстрый рост отношения является ограничением увеличения угловой скорости вращения диска и как следствие ограничения увеличения кинетической энергии системы. Только конструкторские соображения в отношении габаритов конструкции и выбор материала ограничивает величину удельной энергии равнопрочного диска.

Сравнение влияния формы ротора для выбора оптимальной выполним в результате сравнения величин удельных энергий (1), (7), (8), (12). Данный результат показывает, что оптимальной формой диска с максимальной величиной удельной энергии на единицу массы является диск равной прочности с толщиной, изменяющейся по зависимости: 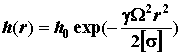. Физико-механические свойства материала диска ротора также определяют величину этой энергии. Материал, у которого величина отношения допускаемого напряжения к плотности материала является наибольшей, то этот материал будет наилучшим материалом для создания ротора [3].

Литература

1. Гулиа Н.В. Инерционные аккумуляторы энергии. Из-во ВГУ, Воронеж,1973г, 240с.

2. Биргер И.А., Мавлютов Р.Р. Сопротивление материалов: Учебное пособие .- М.: Наука. Гл. ред. физ.-мат. лит., 1986.- 560с.

3. Марочник сталей и сплавов/Под ред. А.С. Зубченко. –М.: Машиностроение, 2003. – 672 с.