Карачун В.В., Мельник В.М.

Національний технічний університет України «КПІ»

ОБЧИСЛЕННЯ КРИВИЗНИ ОБОЛОНКИ КАТЕНОЇДНОЇ ФОРМИ

Надалі вважатимемо геометрію оболонки такою, для якої виконується умова [1, 2]

(1)

Ця умова має ту особливість, що містить характерні геометричні параметри.

Беручи до уваги застереження (1), припускаємо, що стала Ламе

(2)

Перетворимо співвідношення (10.25) і (10.26) для обчислення величин та [2]. Маємо:

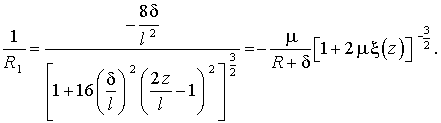(3)

З огляду на основне припущення (1), вираз (3) спрощується:

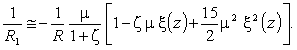(4)

Очевидно, що коли , то і , отже,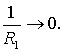

Відповідно до

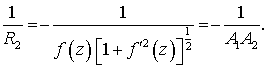
Беручи до уваги вирази [1], дістаємо:

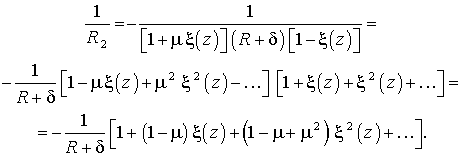(5)

Остаточно маємо:

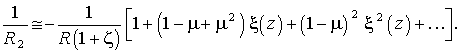
Якщо і то з формули (5)

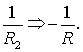
Формули (2), (3) і (5) слушні лише для виконання умови (1).

Проведемо чисельну оцінку можливої геометрії оболонки. Нехай Це достатня опуклість (або угнутість) поверхні. Тоді

Для того, щоб виконувались умови (5) і , потрібно за значної опуклості (або угнутості) брати порівняно протяжні оболонки.

Нехай . Тоді

Якщо

Останній випадок найбільш несприятливий.

Припустимо, що

(6)

Тоді розглядатимемо випадок, коли сталі Ламе визначаються співвідношеннями

(7)

(8)

Спростимо рівняння руху оболонки. Для цього скористаємося припущеннями, сформульованими вище. Крім того, у рівняннях після обчислень з’являться доданки, що містять множники

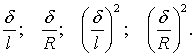
Наявність двох останніх множників дає змогу відкинути відповідні доданки через їх малі значення, тому що

та.

Отже, все рівняння можна звести до такої структури:

зовнішнє збурення + сили інерції.

Література

1. Мельник В.М., Карачун В.В. Шуми і вібрація. Збурюючи чинники та їх характеристики: Навч. посібник. –К.: Техніка, 2008.-352 с.

2. Карачун В.В., Мельник В.М. Задачі супроводу та маскування рухомих об’єктів: (Монографія) / В.В. Карачун, В.М. Мельник; Нац. техн.. ун-т України «КПІ». – Київ, «Корнійчук», 2011. -264с.: іл.. – Бібліогр. с: 261-263