Ýêîíîìè÷åñêèå íàóêè/8. Ìàòåìàòè÷åñêèå
ìåòîäû â ýêîíîìèêå.
Shevchenko Y.T., doctor of sciences Bidyuk P.I.
National Technical University of Ukraine “Kyiv Polytechnic University”,
Ukraine
COMPARATIVE ANALYSIS OF NEURAL NETS AND ARIMA MODELS FOR FORECASTING OF
ECONOMICAL PROCESS
Introduction
Economic processes are difficult to predict but at the
same time it is very important to have a good estimation of economic indicators
forecast not only for government, but also for companies to plan of economic
development in specific country or region to take into account external
factors.
From a statistical point of view neural networks are
interesting because of their potential use in prediction problems. In last ten
years neural networks have received a great deal of attention in many fields of
study [1]. Neural networks are of particular interest because of their ability
to self-train. They are being used in the areas of prediction where regression models
[2] traditionally being used before.
Ward neural net [3], general regression neural net [4]
and polynomial net (variation of Group Method of Data Handling) [5] are objects
of special interest because they are showing good results in probabilistic problems.
Statement of the
problem
Let us take the gross domestic product (GDP) of
Russian Federation as an example of economic process and make several
ARIMA-type models and several neural nets to make short-term prediction.
We will make short-term predictions of price index in
Russian Federation using Gross domestic product and average monthly salary as factors.
The resulting models would be compared by the presence of autocorrelation in
the residuals
using Durbin–Watson
statistic,
by the proportion of
variability in a data set that is accounted for by the statistical model using coefficient of determination R2, by sum of squared errors. The resulting forecasts
would be compared by mean squared error, mean average percent error and Theil
coefficient.
Theory
Generalized Regression Network
A GRN is a variation of the radial basis neural networks. A GRN does not
require an iterative training procedure as back propagation networks. It
approximates any arbitrary function between input and output vectors, drawing the
function estimate directly from the training data.
251658240
Figure 3.1 General Structure of GRN
A GRN consists of four layers: input layer, pattern layer, summation
layer and output layer as shown in figure. 3.1. The number of input units in
input layer depends on the total number of the observation parameters. The
first layer is connected to the pattern layer and in this layer each neuron
presents a training pattern and its output. The pattern layer is connected to
the summation layer. The summation layer has two different types of summation,
which are a single division unit and summation units. The summation and output
layer together perform a normalization of output set. In training of network,
radial basis and linear activation functions are used in hidden and output
layers. Each pattern layer unit is connected to the two neurons in the
summation layer, S and D summation neurons. S summation neuron computes the sum
of weighted responses of the pattern layer. On the other hand, D summation
neuron is used to calculate un-weighted outputs of pattern neurons. The output
layer merely divides the output of each S-summation neuron by that of each
D-summation neuron, yielding the predicted value Y0i to an unknown input vector
x as ;
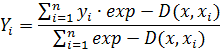
![]()
yi is
the weight connection
between the ith
neuron in the
pattern layer and the
S-summation neuron, n
is the number of the
training patterns, D is the Gaussian function, m is the number of
elements of an input vector,
xk and xik are the
jth element of
x and xi, respectively, r is
the spread parameter,
whose optimal value
is determined experimentally.
Ward network
Ward neural network - multilayer network, in which the inner layers of
neurons are divided into blocks. These networks are used for solving problems
of prediction and classification.
251658240
Figure 3.2 General Structure of Ward net
Topology of ward
net is
1. The input
layer neurons
2. Neurons of the
hidden layer unit
3. The neurons of
output layer
The partition
into blocks of hidden layers allows to use different transfer functions for the
various units of the hidden layer. Thus, the same signals received from the
input layer, weighed and processed in parallel using multiple methods, and the
result is then processed by neurons in the output layer. The use of different
processing methods for the same data set allows us to say that the neural
network analyzes data from various aspects. Practice shows that the network
shows very good results in solving problems of prediction and pattern
recognition. For the input layer neurons, as a rule, set a linear activation
function. Activation function for neurons of the hidden units and output layer
is determined experimentally.
251658240
Figure 3.3 General Structure of GMDH
GMDH Network contains in links polynomial expressions. The result of
training is an opportunity to present the output as a polynomial function of
all or part inputs.
The main idea of GMDH is
that the algorithm tries to construct a function (called a polynomial model),
which would behave in such a way that the predicted output value was as close
as possible to its actual value. For many users are very useful to have a model
capable of predicting exercise using familiar and easy to understand polynomial
equations. In the NeuroShell 2 GMDH neural network is formulated in terms of
architecture, called polynomial network. Nevertheless, the obtained model is a
standard polynomial function.
The GMDH algorithm secures an optimal
structure of the model from successive generations of partial polynomials after
filtering out those intermediate variables that are insignificant for
predicting the correct output. Most
improvement of GMDH has focused on the generation of the partial polynomial,
the determination of its structure and the selection of intermediate
variables. However, every modified GMDH
is still a model-driven approximation, which means that the structure of the
model has to be determined with the aid of empirical (regression)
approaches. Thus the algorithms could
not be said to truly reflect the self-organizing feature that is able to match
the relationship between variables completely based on the prior knowledge.
The computation
experiments.
To construct a prediction for price index first of all evaluation
parameters p, q, d for ARIMA-type models were found using auto-correlation and
particle auto-correlation functions. The time series consisted of 60
observations – monthly values if price index of Russian Federation. Seven
models were built using Eviews 7.0 and Neuroshell 2 software: four ARIMA-type
models and three neural nets. Also indicators of model and indicators of
prediction were calculated to make the comparative analysis of models: Coefficient of determination (R2),
Sum of squared errors, Durbin – Watson statistic, mean absolute error (MAE),
mean absolute percent error(MAPE), Theil coefficient.
Here is the Table with
data based on a sample of 60 values:
Table 4.1
|
Model Type |
Indicators of model |
Indicators of
prediction |
||||
|
Coefficient of determination R2 |
Sum of squared errors |
Durbin – Watson
statistic |
Mean absolute error |
Mean absolute percent
error |
Theil coefficient |
|
|
Auto-regressive
(1,2,4) |
0,8642 |
622833 |
2,2519 |
83,986 |
7,3 |
0,0499 |
|
Auto-regressive with moving
average(ARMA)(1,2,4,6;1,7,11,12) |
0,8683 |
331375 |
2,22 |
154,13 |
10,91 |
0,0796 |
|
Auto-regressive with trend (1,2,3,4,6,11 ; 2) |
0,8789 |
555615 |
2,3992 |
78,62 |
6,62 |
0,0491 |
|
Auto-regressive with
the explanatory variable
1,6,8,9,10,11,12;1,2,8) |
0,7837 |
300061 |
2,483 |
88,94 |
6,5477 |
0,0399 |
|
General regression net |
0,6051 |
2747003 |
0,5546 |
126,6 |
9,4867 |
0,1436 |
|
Ward net |
0,3085 |
4810740 |
0,5528 |
218,13 |
19,61 |
0,19 |
|
Polynomial net (GMDH) |
0,7181 |
1961191 |
0,8138 |
107,67 |
8,3010 |
0,1197 |
From this Table
we can see that neural nets showed worse results than ARIMA-type models.
Results are quite satisfying, but not good enough. So let’s try to build the
same Table for sample of 80 values and compare:
Table 4.2
|
Model Type |
Indicators of model |
Indicators of
prediction |
||||
|
Coefficient of determination R2 |
Sum of squared errors |
Durbin – Watson
statistic |
Mean absolute error |
Mean absolute percent
error |
Theil coefficient |
|
|
Auto-regressive (AR)(1,2,4) |
0,9236 |
1915214 |
2,0312 |
157,24 |
11,7557 |
0,0935 |
|
Auto-regressive with moving average
(1,2,3,4;4,7,8,12) |
0,9478 |
786234 |
2,0655 |
103,58 |
7,1228 |
0,0386 |
|
Auto-regressive with trend(1,2,4 ; 2) |
0,95 |
1250298 |
2,1256 |
110,1 |
8,1255 |
0,051 |
|
Auto-regressive with
the explanatory variable (1,2,3,4;1,2,4,5,12) |
0,93 |
619545 |
2,0354 |
148 |
9,1848 |
0,0461 |
|
General regression net |
0,9317 |
1860480 |
1,2747 |
58,8 |
3,1053 |
0,0846 |
|
Ward net |
0,9297 |
1922640 |
1,0285 |
123,14 |
9,9472 |
0,0738 |
|
Polynomial net (GMDH) |
0,9412 |
1607680 |
2,41 |
87,18 |
6,4027 |
0,0682 |
We see that all models except AR have better results in almost all
indicators. Let’s try to take larger sample and see if results will be even
better:
Let’s now take 100 values:
Table 4.3
|
Model Type |
Indicators of model |
Indicators of
prediction |
||||
|
Coefficient of determination R2 |
Sum of squared errors |
Durbin – Watson
statistic |
Mean absolute error |
Mean absolute percent
error |
Theil coefficient |
|
|
Auto-regressive (AR)(1,9,12) |
0,9792 |
1475356 |
1,8674 |
139,22 |
7,2057 |
0,0477 |
|
Auto-regressive with moving average (1,9,12;3,12) |
0,9839 |
828285 |
2,2546 |
94,31 |
4,6569 |
0,0293 |
|
Auto-regressive with trend(1,9,12 ; 2) |
0,9795 |
14568887 |
1,8897 |
124,61 |
6,768 |
0,0428 |
|
Auto-regressive with
the explanatory variable (1,9,12;4,5,6,12) |
0,9785 |
707169 |
2,4317 |
78,58 |
3,6749 |
0,0207 |
|
General regression net |
0,865 |
11660011 |
0,2579 |
134,42 |
5,0079 |
0,1302 |
|
Ward net |
0,923 |
6647390 |
1,2215 |
158,9 |
8,272 |
0,0841 |
|
Polynomial net GMDH) |
0,8467 |
13235506 |
0,6247 |
188,46 |
9,0948 |
0,1386 |
Comparing with previous sample we see slightly worse indicators of
prediction and better indicators of model, but in general models showed better
results in sample of 80. All neural nets except Ward net showed worse results.
ARIMA – type models showed better result among all indicators. Let’s take one
more sample of 120 values: Let’s take 120 values to find out if results would
be better:
Table 4.4
|
Model Type |
Indicators of model |
Indicators of
prediction |
||||
|
Coefficient of determination R2 |
Sum of squared errors |
Durbin – Watson
statistic |
Mean absolute error |
Mean absolute percent
error |
Theil coefficient |
|
|
Auto-regressive (AR) (1,7,9) |
0,9523 |
5629700 |
2,3384 |
289,93 |
16,99 |
0,075 |
|
Auto-regressive with moving average (1,5,7,8;1,10,11,12) |
0,9518 |
4034816 |
2,1762 |
239,79 |
12,48 |
0,059 |
|
Auto-regressive with trend(1,7,9;2) |
0,9526 |
5341754 |
2,238 |
213,36 |
10,52 |
0,0634 |
|
Auto-regressive with
the explanatory variable (1,9,12;1,2,3,6) |
0,9665 |
1676531 |
1,9746 |
310.92 |
11,76 |
0,0671 |
|
General regression net |
0,9304 |
9466440 |
0,925 |
216,83 |
14,34 |
0,0894 |
|
Ward net |
0,8624 |
18718440 |
0,766 |
318,22 |
17,57 |
0,1291 |
|
Polynomial net GMDH) |
0,9156 |
11488080 |
0,881 |
192,38 |
9,126 |
0,0942 |
All models showed worse results. The next step is to determine the best
sample: best results during our computations showed general regression net,
worst results showed auto-regressive model. Let’s compare coefficient of
determination and mean absolute percent error (MAPE) for them on
different samples:
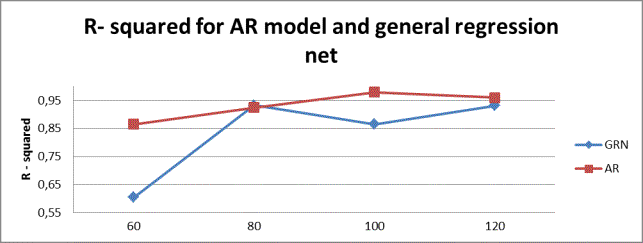 Figure 4.1 R- squared for
auto-regressive model and general regression net
Figure 4.1 R- squared for
auto-regressive model and general regression net
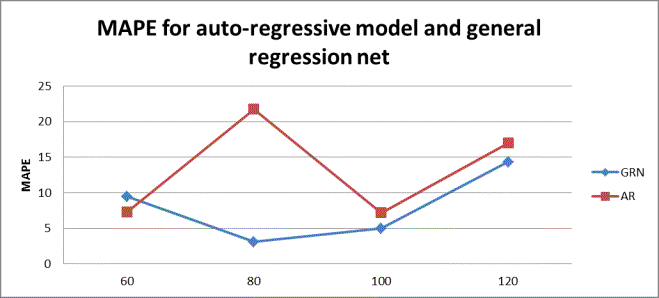
Figure 4.2 MAPE for
auto-regressive model and general regression net
It is hard to say what sample showed better results for economical
process, but we can see small mean absolute percent error for sample of 100
values, thus we can conclude that this sample was best.
So we found out what sample is best for each process and what models
show best and worse results. Our last step is to make short-term forecast for
process:
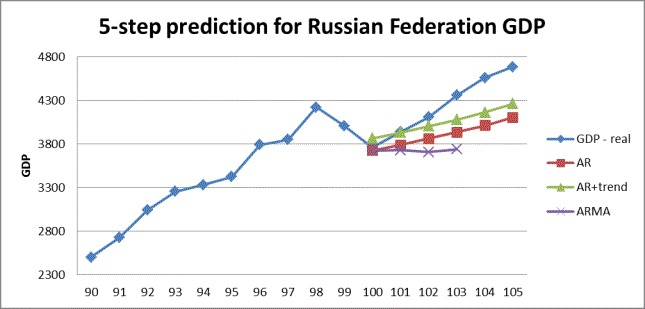
Figure 4.3 5-step prediction for
Russian Federation GDP
4.Conclusion
The best results were obtained using general regression net and
polynomial net while the worst results were obtained by auto-regression model.
Analysis of the obtained results of the study shows that in general
forecasted values obtained by neural networks are closer to the
source statistics than results obtained by ARIMA-type models. In our opinion,
this is due to the fact that neural networks designed for application to the
series that have complex and nonlinear structure, while the ARIMA-type models
designed to work with rows that have more noticeable structural patterns.
5. Literature
1.
Brad Warner, Manavendra Misra
Understanding Neural Networks as Statistical Tools: The American Statistician
Vol. 50, No. 4 (Nov., 1996), pp. 284-293
2.
Áèäþê Ï.È., Ðîìàíåíêî Â.Ä., Òèìîùóê Î.Ë., Ó÷åáíîå ïîñîáèå ïî "Àíàëèçó âðåìåííûõ ðÿäîâ" - ÍÒÓÓ
"ÊÏÈ", 2010, 230 ñ.
3.
Group Method of Data
Handling / Web address: http://www.gmdh.net/
4.
GMDH Wiki/ Web address: http://opengmdh.org/wiki/GMDH_Wiki