Петришин Т. Р.

Национальный технический университет Украины “КПИ”

Применение рециркуляционных нейронных сетей для обработки изображений

Рециркуляционные нейронные сети представляют собой многослойные нейронные сети с обратным распространение информации. При этом обратное распространение информации происходит по двунаправленным связям, которые имеют в различных направлениях разные весовые коэффициенты. При обратном распространении сигналов, в таких сетях осуществляется преобразование их с целью восстановления входного образа. В случае прямого распространения сигналов происходит сжатие входных данных. Обучение рециркуляционных сетей производится без учителя. Рециркуляционные сети характеризуются как прямым Y=f(X), так и обратным X=f(Y) преобразованием информации. Задачей такого преобразования является достижение наилучшего автопрогноза или самовоспроизводимости вектора X. Рециркуляционные нейронные сети применяются для сжатия (прямое преобразование) и восстановления исходной (обратное преобразование) информации. Такие сети являются самоорганизующимися в процессе работы. Они были предложены в 1988 году. Теоретической основой рециркуляционных нейронных сетей является анализ главных компонент. Метод главных компонент применяется в статистике для сжатия информации без существенных потерь ее информативности. Он состоит в линейном ортогональном преобразовании входного вектора X размерности n в выходной вектор Y размерности p, где p<n. При этом компоненты вектора Y являются некоррелированными и общая дисперсия после преобразования остается неизменной. Совокупность входных паттернов представим в виде матрицы:

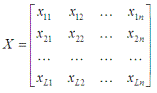
где

соответствует k-му входному образу, L — общее количество образов. Будем считать, что матрица X является центрированной, то есть вектор математических ожиданий µ=0. Этого добиваются при помощи следующих преобразований:

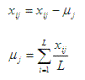
Матрица ковариаций входных данных X определяется как

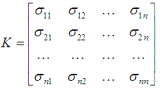
где σij — ковариация между i-ой и j-ой компонентой входных образов. Элементы матрицы ковариаций можно вычислить следующим образом:

где i,j = 1,…,n.
Метод главных компонент состоит в нахождении таких линейных комбинаций исходных переменных

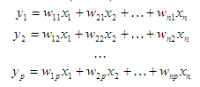
что

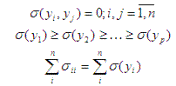
Из последних выражений следует, что переменные уi некоррелированы, упорядочены по возрастанию дисперсии и сумма дисперсий входных образов остается без изменений. Тогда подмножество первых р переменных у характеризует большую часть общей дисперсии. В результате получается представление входной информации.Переменные у, i = 1,…,p называются главными компонентами. В матричной форме преобразование главных компонент можно представить как

где строки матрицы W^T должны удовлетворять условию ортогональности, т.е

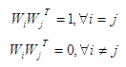
при этом вектор W_i определяется как

Для определения главных компонент необходимо определить весовые коэффициенты W_i,j = 1,…,p. Рециркуляционная нейронная сеть представляет собой совокупность двух слоев нейронных элементов, которые соединены между собой двунаправленными связями.

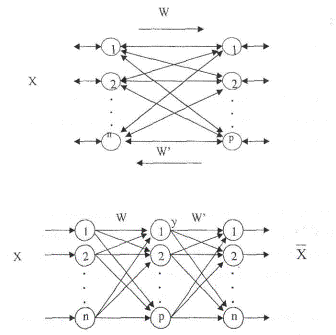
Каждый из слоев нейронных элементов может использоваться в качестве входного или выходного. Если слой нейронных элементов служит в качестве входного, то он выполняет распределительные функции. В противном случае нейронные элементы слоя являются обрабатывающими. Весовые коэффициенты соответствующие прямым и обратным связям характеризуются матрицей весовых коэффициентов W и W’. Для наглядности, рециркуляционную сеть можно представить в развернутом виде. Такое представление сети является эквивалентным и характеризует полный цикл преобразования информации. При этом промежуточный слой нейронных элементов производит кодирование (сжатие) входных данных X, а последний слой осуществляет восстановление сжатой информации Y. Назовем слой нейронной сети, соответствующий матрице связи W прямым, а соответствующий матрице связей W’ — обратным. Рециркуляционная сеть предназначена как для сжатия данных, так и для восстановления сжатой информации. Сжатие данных осуществляется при прямом преобразовании информации в соответствие с выражением:

Восстановление или реконструкция данных происходит при обратном преобразовании информации:

В качестве функции активации нейронных элементов F может использоваться как линейная, так и нелинейная функции. При использовании линейной функции активации:

Линейные рециркуляционные сети, в которых весовые коэффициенты определяются в соответствии с методом главных компонент называются РСА сетями. Рециркуляционные нейронные сети можно применять для сжатия и восстановления изображений. Изображение делится на блоки. Блок называется окном, которому в соответствие ставится рециркуляционная нейронная сеть. Количество нейронов первого слоя сети соответствует размерности окна (количеству пикселей). Сканируя изображение при помощи окна и подавая его на нейронную сеть, можно сжать входное изображение.