МАКАРИЧЕВ А.В.

Харьковский национальный автомобильно-дорожный университет (ХАДИ)

О ВЕРОЯТНОСТИ ИСПРАВНОСТИ В ТЕЧЕНИЕ ОПРЕДЕЛЕННОГО ВРЕМЕНИ СИСТЕМ В КОМПЛЕКСАХ И КОМПЛЕКСОВ С БЫСТРЫМ ОБСЛУЖИВАНИЕМ ПРИ ЛЮБОЙ ДОПУСТИМОЙ НАГРУЗКЕ

Рассмотрим комплекс , в котором работают однотипных восстанавливаемых систем. С течением времени в каждой восстанавливаемой системе может возникнуть требование на обслуживание элемента из этой системы. Поток таких требований из каждой системы является пуассоновским с параметром . В момент отказа элемента в одной из систем возникает требование на его обслуживание, которое немедленно поступает в ремонтный орган (РО), где осуществляется восстановление элемента в порядке поступления его на обслуживание. Восстановленный элемент возвращается в ту систему, в которой произошел его отказ, а требование на обслуживание немедленно покидает РО.

Длины требований (различных элементов или различных отказов одного и того же элемента) есть независимые положительные случайные величины. Обозначим - функцию распределения длины требования по обслуживанию отказавшего элемента. Ее й момент обозначим . Состояние комплекса описывает случайный процесс

,

где - число неисправных элементов в й системе. Отказ системы наступает, когда число неисправных элементов в ней меняется с на . Восстановление системы происходит, если число неисправных элементов в ней меняется с на . Пусть - множество исправных, а - множество неисправных состояний й системы.

Случайный процесс является регенерирующим. Моментами регенерации являются моменты перехода случайного процесса в состояние

,

когда все элементы всех систем комплекса исправны.

Пусть - суммарная нагрузка на РО всех систем комплекса, , и - стационарные времена ожидания начала обслуживания в порядке поступления требований в системе с входящим пуассоновским потоком соответственно с параметрами и и одной той же функцией распределения времени обслуживания , , , - функция стационарного распределения времени пребывания в системе с нагрузкой с входящим пуассоновским потоком с параметром и функцией распределения времени обслуживания , . Пусть .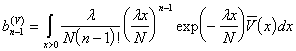

.

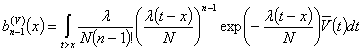Обозначим - вероятность исправности определенной -й системы комплекса в течение времени в стационарном режиме. Пусть - вероятность исправности определенной -й системы комплекса в течение времени в стационарном режиме.

Теорема 1. Пусть и существует конечный момент . Тогда при

и , где

,

,

.

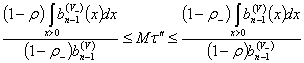Литература.

1.Макаричев А.В. Об оценках вероятности отказа системы на периоде регенерации комплекса восстанавливаемых систем. Кибернетика и системный анализ, 1995, № 6, c. 170-172.

2.Соловьёв А.Д. Асимптотическое поведение момента первого наступления редкого события в регенерирующем процессе// Известия АН СССР. Техническая кибернетика, 1971, № 6, с. 79-89.

3.Соловьёв А.Д. Оценка надёжности восстанавливаемых систем. М.: Знание, 1987, 60 с.