Математика/ 5. Математичне моделювання

к.ф.-м.н. Готинчан І. З

Чернівецький торговельно-економічний інститут КНТЕУ, Україна

Готинчан Г. І.

Чернівецький факультет НТУ «ХПІ», Україна

Інтегральне перетворення, породжене гібридним диференціальним оператором (Конторовича-Лєбєдєва) - Фур’є- Лежандра - Ейлера на сегменті полярної осі

Постановка проблеми та аналіз публікацій за темою дослідження.

Метод гібридних інтегральних перетворень, започаткований в роботі Я.С. Уфлянда [1] й розвинутий та математично обґрунтований в роботі [2], є одним із ефективних методів побудови точного аналітичного розв'язку алгоритмічною характеру задач математичної фізики неоднорідних середовищ. Це дало змогу алгебраїзувати сепаратні системи лінійних диференціальних рівнянь з частинними похідними.

Ціль статті. Дана стаття присвячена запровадженню інтегрального перетворенню, породженого на полярній осі з трьома точками спряження гібридним диференціальним оператором (Конторовича – Лєбєдєва) - Фур’є – Лежандра - Ейлера.

Основна частина. Запровадимо методом дельта-подібної послідовності (ядро Діріхле) інтегральне перетворення, породжене на множині гібридним диференціальним оператором (ГДО)

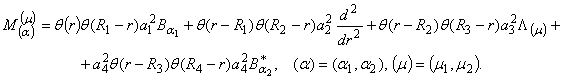(1)

Тут - одинична функція Гевісайда [3], - диференціальний оператор Ейлера [4], - диференціальний оператор Фур’є [4], - диференціальний оператор Бесселя [2], 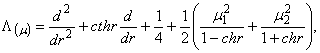- узагальнений диференціальний оператор Лежандра [2]; .

Означення. Областю визначення ГДО назвемо множину G вектор-функцій з такими властивостями:

1) вектор-функція неперервна на множині

2) функції задовольняють крайові умови

(2)

3) функції задовольняють умови спряження

(3)

Оскільки ГДО самоспряжений і має одну особливу точку , то його спектр дійсний та неперервний [2]. Можна вважати, що спектральний параметр Йому відповідає дійсна спектральна вектор-функція

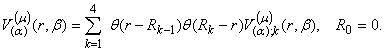(4)

При цьому функції повинні задовольняти відповідно диференціальні рівняння

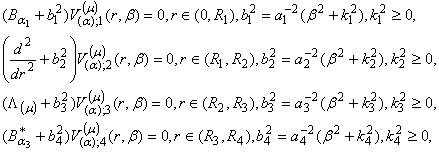(5)

крайові умови (2) та умови спряження (3).

В силу лінійності спектральної задачі Штурма-Ліувілля (5), (2), (3) функції будемо відшукувати як лінійну комбінацію фундаментальної системи розв’язків:

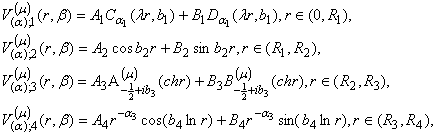(6)

Крайова умова (2) в точці та умови спряження (3) для визначення восьми величин дають алгебраїчну систему семи рівнянь:

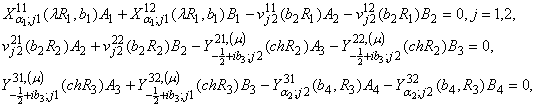(7)

Алгебраїчна система (7) сумісна [5]. У результаті стандартного розв'язання алгебраїчної системи (7) й підстановки одержаних значень та у рівності (6) маємо функції:

(8)

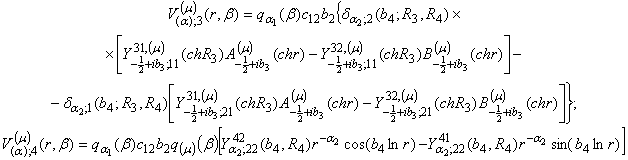У рівностях (8) беруть участь функції:

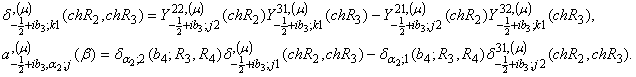
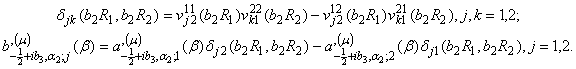
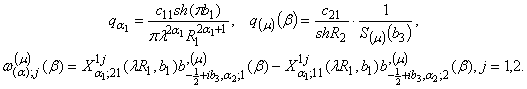
Всі інші функції загальноприйняті [2].

Визначимо величини:

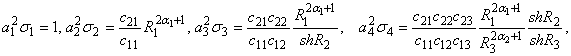
вагову функцію

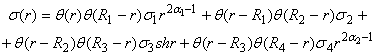
та спектральну щільність

Наявність вагової функції , спектральної функції , та спектральної щільності дозволяє визначити пряме та обернене гібридне інтегральне перетворення (ГІП), породжене на множині ГДО , визначеного рівністю (1) :

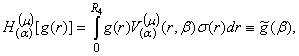(9)

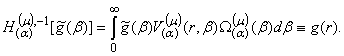(10)

Математичним обґрунтуванням правил (9), (10) є твердження.

Теорема 1 (про інтегральне зображення). Якщо вектор – функція

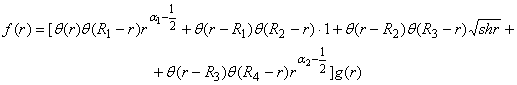
неперервна, абсолютно сумовна й має обмежену варіацію на множині , то для будь-якого справджується інтегральне зображення:

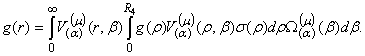(11)

Доведення: Доведення теореми базується на значенні подвійного невласного інтегралу

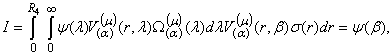(12)

якщо , та дорівнює нулю, якщо . Функція забезпечує абсолютну й рівномірну збіжність інтеграла по . Рівність (12) отримуємо методом дельта-подібної послідовності (ядро Діріхле) [6].

Припустимо тепер, що функція

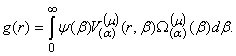(13)

Помножимо рівність (13) на вираз і проінтегруємо по від до В силу рівності (12) отримуємо:

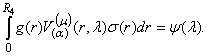(14)

Підставивши в (13) функцію

,

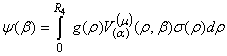приходимо до інтегрального зображення (11).

Доведення теореми завершено.

Введемо до розгляду величини та функції:

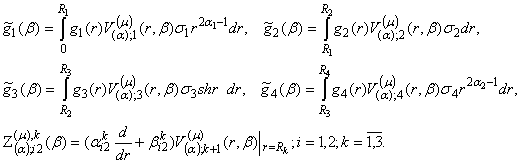
Теорема 2 (про основну тотожність). Якщо вектор-функція

неперервна на множині , а функції задовольняють крайові умови

(15)

та умови спряження

(16)

то має місце основна тотожність ГІП ГДО :

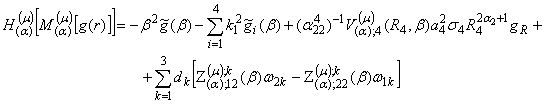(17)

Доведення теореми здійснюється за відомою логічною схемою [6].

Висновок: Одержані правила (9), (10) та (17) складають достатньо ефективний математичний апарат для одержання інтегрального зображення точних аналітичних розв'язків алгоритмічного характеру відповідних стаціонарних і не стаціонарних задач математичної фізики кусково-однорідних середовищ.

Література:

1. Уфлянд Я. С. О некоторых новых интегральных преобразованиях и их приложениях к задачам математической физики / Я.С. Уфлянд //Вопросы математической физики. - Л., 1976.- С.93-106.

2. Ленюк М.П. Гібридні інтегральні перетворення (Фур'є, Бесселя, Лежандра). Частина 1/ М.П. Ленюк, М. І. Шинкарик. – Тернопіль: Економ. думка, 2004.-368с.

3. Шилов Г.Е. Математический анализ. Второй специальний курс. / Г.Е. Шилов. – М.: Наука, 1965. – 328с.

4. Степанов В.В. Курс дифференциальных уравнений / В.В. Степанов -М.: Физматгиз, 1959.-468с.

5. Курош А.Г. Курс высшей алгебры. / А.Г. Курош – М.: Наука, 1971. – 432с.

6. Ленюк М.П. Гібридні інтегральні перетворення типу Ейлера-(Фур'є, Бесселя) / М.П. Ленюк. – Львів,2009.-76с.-(Препринт/НАН України. Інститут прикладних проблем механіки і математики ім. Я. С. Підстригача; 02.09) – Чернівці: Прут, 2009.-76с.