Математика/5. Математическое моделирование
Джамиева Б., Мамешов Б.
Южно-Казахстанский государственный
университет им. М. Ауэзова
Моделирование течения
двухфазной среды в трубе переменного сечения при наличии фазовых превращений
Многофазные
(или гетерогенные), в частности, двухфазные дисперсные системы часто
встречаются в различных областях современной техники и человеческой
деятельности. При этом течение таких сред в большинстве случаев сопровождается
тепломассообменными процессами и является одной из актуальных проблем динамики
и теплофизики многофазных систем [1-4].
В рамках
механики многофазных сред [1] стационарное движение двухфазной парокапельной среды в квазиодномерном приближении описывается следующей системой
уравнений:
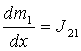 ,
, 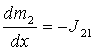 ,
, 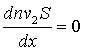 (1)
(1)
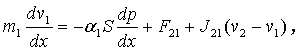
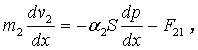 (2)
(2)
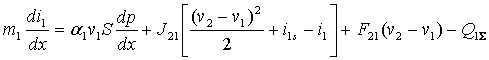 , (3)
, (3)
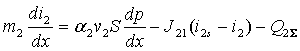 , (4)
, (4)
![]() ,
, ![]() ;
;
![]() ,
, ![]() (5)
(5)
Здесь нижние индексы 1 и 2
относятся к параметрам газовой и конденсированной фаз соответственно; ![]() - истинная и приведенная плотности, объемное содержание,
скорость и энтальпия фаз; p, n, d – давление
в газе, концентрация и диаметр капель; x, S(x) – продольная координата и площадь поперечного
сечения канала;
- истинная и приведенная плотности, объемное содержание,
скорость и энтальпия фаз; p, n, d – давление
в газе, концентрация и диаметр капель; x, S(x) – продольная координата и площадь поперечного
сечения канала; ![]() - энтальпии фаз в
состоянии насыщения;
- энтальпии фаз в
состоянии насыщения; ![]() ,
,![]() ,
,![]() ,
,![]() - соответственно интенсивность фазовых превращений, сила
вязкого трения между газом и каплей, а также интенсивности оттока тепла от газа
и основной массы капли к межфазной поверхности в единицу времени на единице
длины канала. Уравнения (1) это уравнения неразрывности фаз и уравнение
сохранения числа дисперсных капель, уравнения (2) – уравнения сохранения
импульсов фаз, уравнения (3), (4) – уравнения сохранения энтальпий фаз.
Отметим, что при записи уравнений сохранения энтальпий фаз использована
трехтемпературная схема, когда температура межфазной поверхности отличается от
температур газа и основной массы капли.
- соответственно интенсивность фазовых превращений, сила
вязкого трения между газом и каплей, а также интенсивности оттока тепла от газа
и основной массы капли к межфазной поверхности в единицу времени на единице
длины канала. Уравнения (1) это уравнения неразрывности фаз и уравнение
сохранения числа дисперсных капель, уравнения (2) – уравнения сохранения
импульсов фаз, уравнения (3), (4) – уравнения сохранения энтальпий фаз.
Отметим, что при записи уравнений сохранения энтальпий фаз использована
трехтемпературная схема, когда температура межфазной поверхности отличается от
температур газа и основной массы капли.
Для
замыкания системы (1)-(5) необходимо добавить термодинамические уравнения
состояния фаз. При этом газ будем считать калорически совершенным с постоянной
теплоемкостью, а капли – несжимаемыми. Тогда в соответствии с положениями
раздела 1 будем иметь
![]() ,
, ![]() , (6)
, (6)
![]() ,
,
где ![]() - температуры и
теплоемкости газа (при постоянном давлении) (k=1) и капель (k=2); R –
газовая постоянная;
- температуры и
теплоемкости газа (при постоянном давлении) (k=1) и капель (k=2); R –
газовая постоянная; ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры среды в
некотором фиксированном (начальном) состоянии, относительно которого отсчитываются
все изменения. Следует иметь в виду, что энтальпия пара в общем случае зависит
от давления и связана с энтальпией жидкой фазы. В случаях, когда давление и
температура меняются не в очень широких диапазонах, а сами давления не очень
высоки, можно обойтись моделью калорически совершенного газа (6). При этом
необходимое условие пригодности (6) обеспечивается, если зависимость для
теплоты парообразования описывается следующей формулой [1]:
- параметры среды в
некотором фиксированном (начальном) состоянии, относительно которого отсчитываются
все изменения. Следует иметь в виду, что энтальпия пара в общем случае зависит
от давления и связана с энтальпией жидкой фазы. В случаях, когда давление и
температура меняются не в очень широких диапазонах, а сами давления не очень
высоки, можно обойтись моделью калорически совершенного газа (6). При этом
необходимое условие пригодности (6) обеспечивается, если зависимость для
теплоты парообразования описывается следующей формулой [1]:
![]() ,
,
Здесь ![]() и
и ![]() - температура
насыщения и теплота парообразования. В достаточно широком диапазоне изменения
параметров p и T можно
использовать аппроксимацию
- температура
насыщения и теплота парообразования. В достаточно широком диапазоне изменения
параметров p и T можно
использовать аппроксимацию
![]() (7)
(7)
где ![]() ,
, ![]() - аппроксимационные
параметры. Для
- аппроксимационные
параметры. Для ![]() ,
, ![]() и
и ![]() воспользуемся
формулами
воспользуемся
формулами
![]() ,
, ![]() ,
, ![]() . (8)
. (8)
Силу
вязкого взаимодействия капли с несущей средой ![]() и интенсивности
теплообмена
и интенсивности
теплообмена ![]() ,
, ![]() зададим следующими
формулами [1,2]:
зададим следующими
формулами [1,2]:
![]() ,
, ![]() , (9)
, (9)
![]()
Здесь ![]() ,
,![]() - коэффициенты теплопроводности газа и капель;
- коэффициенты теплопроводности газа и капель; ![]() - температура
межфазной поверхности, которую обычно можно принять равной температуре
насыщения
- температура
межфазной поверхности, которую обычно можно принять равной температуре
насыщения ![]() . Для коэффициента сопротивления капли
. Для коэффициента сопротивления капли ![]() и чисел Нуссельта
и чисел Нуссельта ![]() ,
, ![]() можно использовать
известные выражения [1,2].
можно использовать
известные выражения [1,2].
При
заданных параметрах на входе трубы
х=0: ![]() =
= ![]() ,
, ![]() (10)
(10)
распределение параметров вдоль трубы длиной L (0≤х≤L) находится путем решения задачи Коши (1)-(10).
Складывая
оба уравнения масс фаз (1) получим интеграл массы или расхода смеси ![]() . Имеет место также интеграл энергии смеси
. Имеет место также интеграл энергии смеси
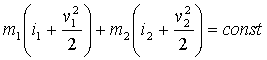
Эти первые
интегралы можно использовать, в частности, для проверки решений поставленной
задачи Коши. Комбинируя уравнения системы (1)-(5) можно получить уравнение
отдельно для давления, которое имеет вид
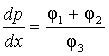 ,
,
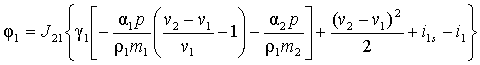 ,
,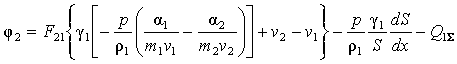 ,
,
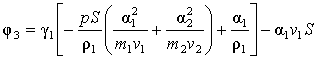 ,
, 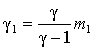
Здесь ![]() - показатель адиабаты
газовой фазы. В качестве характерной длины задачи
- показатель адиабаты
газовой фазы. В качестве характерной длины задачи ![]() выбиралась
минимальная среди характерных длин выравнивания скоростей
выбиралась
минимальная среди характерных длин выравнивания скоростей ![]() , температур
, температур ![]() капли и газа и длины
трубы L
капли и газа и длины
трубы L
![]()
Литература:
1.
Нигматулин Р.И. Динамика
многофазных сред. - М.: Наука, 1987.
2.
Ивандаев А.И., Кутушев
А.Г., Нигматулин Р.И. Газовая динамика многофазных сред//Итоги науки и техники.
Сер. Механика жидкости и газа. Т.16. М.: ВИНИТИ, 1981.
3.
Пирумов У.Г. Перспективные
методы получения ультрадисперсных частиц в высоскоростных потоках // Проблемы
машиностроения и надежности. – 1996. - №1. – С. 94-116.
4. Аникеев В.И., Степанов Д.А., Ермакова А. Моделирование и расчет процесса быстрого расширения сверхкритического флюида с образованием наночастиц // Теоретич. основы хим. технологии. –2011.–Т.45,№2. –С.155-169.