Математика/Прикладная математика
Студент Сапожникова Е.Ю.
Одесский
Национальный Университет им.И.И. Мечникова, Украина
Элементы теории повторных
и
двойных рядов
Актуальность изучения данной проблемы обусловлена тем, что раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией повторных и двойных рядов.
Пусть задано бесконечное множество чисел 
(
=1,2,3,….) зависящих от двух натуральных индексов. Представим
себе это множество в виде матрице
……………. 
….
……………. 
…. (1)
…………………………………………………..
……………. 
….
...............................................................................
Матрица
такого рода называется бесконечной прямоугольной матрицей с двумя входами.
Понятие повторного ряда связано с рассмотрение матриц данного вида.
Итак, в результате суммирования каждой строки матрицы
в отдельности получаем бесконечную последовательность рядов вида
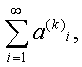(2)
Просуммировав эту последовательность
вторично получим
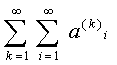(3)
Данный символ называется повторным рядом.
Если же просуммировать элементы матрице по столбцам то получим то получим
повторный ряд вида
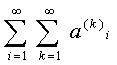(4)
По
аналогии с простыми рядами вводим понятие сходимости для повторного ряда:
Повторный ряд (3) называется сходящимся если:
1)Все ряды вида (2) сходятся к 
, 
;
2)
Сходиться ряд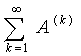 
к некоторому числу 
, где 
и будет сум
повторного ряда.
Члены бесконечной матрице можно различными способами
представить в виде последовательности
(5)
и составить просто ряд
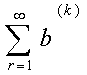(6)
Обратно, если
имеем обыкновенную последовательность
(1.5), то разбив все ее члены (не считаясь с их расположение) на бесконечное
множество бесконечных групп, можно ее представить многими способами в виде
матрицы с двумя входами (1), и по этой матрице составить повторный ряд (3).
Рассмотрим некоторые вопросы сходимости
повторных рядов
Теорема
1. Если ряд (2) сходится абсолютно к
сумме 
, то независимо от расположения его членов в виде матрицы (1)
сходиться и повторный ряд (3), и имеет ту же сумму.
Заметим, что некоторые
строки или столбцы матрицы (1) могут
содержать конечное число членов.
Теорема 2. Пусть дан повторный ряд (3). Если после замены его
членов их абсолютными величинами получается сходящийся ряд, то сходиться не только ряд (3) но и простой ряд (6) состоящий из тех же
членов, что и повторный ряд (3) расположенных в произвольном порядке, и притом
к той же сумме.
Теорема 3. Пусть дана матрица (1). Если по замене членов ряда (3)
их абсолютными величинами получается сходящийся ряд, то сходятся оба повторных
ряда и имеют ту же сумму:
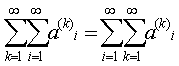
Введем
понятие двойного ряда.
Выражение
вида
+ 
+ 
+ …………….
+ 
+ ….
+ 
+ 
+ ……………. + 
+ …. (7)
………………………………………………..
+ 
+ 
+ ……………. + 
+ ….
+......................................................................=
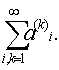
составленное из элементов бесконечной прямоугольной матрицы называется двойным рядом.
Рассмотрим конечную сумму
содержащуюся в первых m
столбцах и первых n
строках
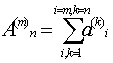
называемую частичной суммой
данного ряда. Устремим m и n в бесконечность.
=
m→∞
n→∞
Полученный
предел называется суммой двойного ряда,
и пишут
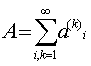
Ряд (7)
называется сходящимся, если он имеет конечную сумму, в противном случае – расходящимся.
Необходимым условием
сходимости двойного ряда является стремление к 0 общего члена
i→∞
k→∞
Это сразу видно из формулы
При нарушение
этого условия ряд заведомо расходиться. Однако
важно подчеркнуть, что это условие не является само по себе достаточным
для сходимости ряда. Иными словами, даже при выполнение этого условия ряд может
расходиться.
Естественно
сопоставить двойной ряд (7) с
повторными рядами (3) и (4). Так как
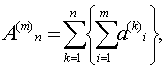
то при фиксированном n переходя к пределу при 
получим
Следовательно суммой повторного
ряда (1.3) является повторный предел
Теорема 4. Если
1) Сходиться двойной
ряд (7)
2) Сходятся все ряды по строкам, то сходиться повторный ряд (3) и имеет ту же сумму, что и двойной
ряд
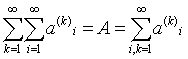
Аналогичная
теорема имеет место и для второго повторного ряда (4)
Вопрос о сходимости двойного ряда (7) просто решается
для случая положительного ряда: 
Теорема 5.
(Критерий сходимости)
Для сходимости ряда (7), если 
необходимо и достаточно, чтобы его частичные суммы были ограничены.
Теорема 7. Пусть дан двойной
ряд (7) и простой ряд (6)
состоящие из одних и тех же членов. Тогда абсолютная сходимость одного из них
влечет за собой абсолютную сходимость другого и равенство их сумм.
Следствие: Пусть матрица (1) и
последовательность (5) состоят из одних и тех же элементов. Тогда повторные
ряды (3), (4), двойной ряд (7) и простой ряд (6) – если хоть один из них
оказывается сходящимся по замене его членов их абсолютными величинами - все четыре сходятся и имеют одну и ту же сумму.
СПИСОК ЛИТЕРАТУРЫ
1.
Кудрявцев Л.Д. Курс
Математического анализа / Л.Д. Кудрявцев – М.: Высшая школа, 1988. – 576с. –
(т.2)
2.
Фихтенгольц Г.М. Курс
дифференциального и интегрального исчисления / Г.М. Фихтенгольц –М.: Наука,
1969. – 800с. – (т.2)