РЕГРЕССИОННЫЕ МЕТОДЫ ИДЕНТИФИКАЦИИ

ЭРГАТИЧЕСКОЙ СИСТЕМЫ

Гарькина И.А., Данилов А.М.

При синтезе сложных динамических систем, в том числе эргатических, возникает непростая задача выделения их элементов по данным нормального функционирования (так, по записи хорового исполнения нельзя определить конкретных исполнителей без их индивидуальных характеристик; по осциллограммам колебаний многозвенной конструкции также нельзя выделить конкретные источники вибрации и т.д.).

В структурной схеме эргатической системы (рис.1) по каждому из каналов управления оператор представляется в виде трех звеньев. Первое характеризует двигательную (моторную) систему человека; другое – формирование мысленного образа выходной координаты; третье – сравнивающее «устройство» центральной нервной системы и формирование ошибки управления. Наибольшие трудности связаны с формализацией сравнивающего «устройства». Это приводит к тому, что при сравнении функционирования систем «оператор-объект управления» и «оператор-имитатор» нельзя установить их отличительные признаки, а именно составляющих: первой, определяемой разницей технических частей этих эргатических систем и второй, определяемой разницей в поведении человека. Именно это обстоятельство, а также то, что в соответствии с организмическим принципом объект, по существу, предопределяет поведение оператора, являются основным тормозом при разработке тренажных и обучающих комплексов.

В этих условиях задача определения управляющих воздействий оператора (стабилизация программного движения без флуктуаций в его поведении) может быть решена в основном лишь с использованием некоторой итерационной процедуры. Это относится и к определению передаточных функций объекта и оператора по данным нормальной эксплуатации. Как видим, прямая идентификация эргатической системы в силу ее замкнутости через человека встречает, по существу, непреодолимые трудности.

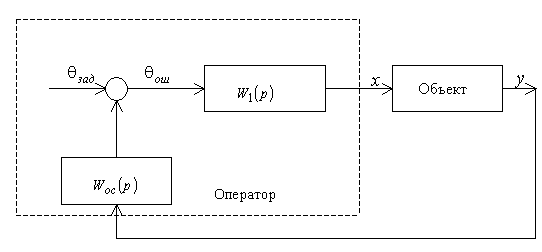
Рис.1.Структурная схема эргатической системы

Классическим, традиционным считается определение оценки передаточных функций по спектральным характеристикам. Однако наблюдается большая расходимость результатов в зависимости от параметров дискретизации, длительности рассматриваемых реализаций и применяемых для сглаживания различных типов «окон» (с неизбежными элементами субъективизма при их выборе).

Известно, что точность определения передаточных характеристик вдали от доминирующих частот крайне низка. Правда, в этих зонах высокая точность и не нужна: оператор управляет объектом на частотах, близких к его собственной частоте. На это обращалось внимание и ранее; учитывалась связь входного сигнала со спектральной характеристикой [1]. Зоны доминирующих частот для некоторых режимов функционирования могут определяться на основе обобщенных АЧХ и ФЧХ, вычисленных решением уравнений идентификации; в этих зонах возможна их линейная аппроксимация. Это говорит о том, что оператор воспринимает объект как усилительное звено с запаздыванием. Но, по-видимому, частотные, впрочем, равно и другие методы, практически не позволяют определить передаточные функции объекта по данным нормальной эксплуатации эргатической системы. Так что решение общей задачи идентификации не позволяет получить требуемые данные для доводки имитаторов объекта с целью сближения стиля управления оператора в условиях реального объекта и его имитатора. Поэтому целесообразней решение частной задачи идентификации, используя для уточнения оценок передаточных функций итерационный метод. Наиболее удобны для использования регрессионные методы параметрической идентификации. Неплохие результаты дает метод наименьших произведений, который, по существу, является обобщением регрессионного метода. Возможно обобщение регрессионного метода идентификации для инерционного оператора с чистым запаздыванием. В этом случае возможна идентификация переменных коэффициентов в уравнениях движения (аппроксимация с использованием полиномов Ньютона или методом наименьших квадратов). После определения уравнений движения, естественно, легко установить и требуемые характеристики оператора.

Пусть в эргатической системе

по синхронным измерениям в процессе нормальной эксплуатации требуется определить матрицу P; . В дискретной форме получим:

, .

Можно показать, что

;

,

, .

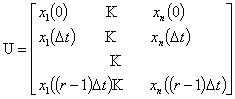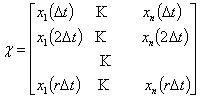В более общем случае, когда оператор представляет собой инерционное звено второго порядка с запаздыванием и при формировании управляющих воздействий использует как фазовые координаты, так и скорости, ускорения будем иметь:

;

в дискретной форме:

;

,

; .

Тогда в соответствии с предыдущим

;

,

.

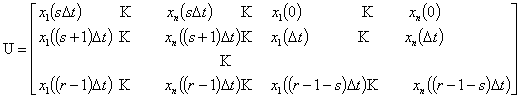Оптимальное управление в системе определится из условия минимума выбранного некоторого функционала качества (структура таких функционалов, в частности указывается в [2]).

Литература

1. Красовский А.А. Системы автоматического управления летательных аппаратов / А.А.Красовский, Ю.А.Вавилов, А.И.Сучков. –М.: Изд. ВВИА им.проф. Н.Е.Жуковского, 1986. – 478 с.

2. Данилов А.М. Математическое моделирование управляющих воздействий оператора в эргатической системе [Текст] / Данилов А.М., Домке Э.Р., Гарькина И.А. // Вестник МАДИ, №2, 2011. –С.18-23.