Гапчак Т.Г., Чехівська І.П.

Вінницький національний аграрний університет, Україна

КОРЕЛЯЦІЙНИЙ АНАЛІЗ У ДОСЛІДЖЕННЯХ БАГАТОФАКТОРНИХ ПРОЦЕСІВ І ЯВИЩ

В умовах сьогодення одним з найбільш загальних законів об’єктивного світу є закон зв’язку і залежності між явищами суспільного життя. Ці явища найбільш складні, оскільки вони формуються під дією багаточисельних, різноманітних і взаємозв’язаних чинників.

Одним із важливих завдань аналізу даних є пошук та оцінка взаємозв'язків між окремими ознаками для певної сукупності об'єктів. Якщо певному значенню однієї величини відповідає сукупність значень другої, то між цими двома величинами існує кореляційний зв'язок. Він зустрічається тоді, коли на досліджуване явище впливає не один, а багато факторів. Оскільки явища суспільного життя складні та багатофакторні, зв'язок між ознаками практично завжди кореляційний [2].

Кореляційні зв’язки, як відомо, не є суворо однозначними. Це зв'язки, при яких кожному значенню факторної ознаки, відповідає декілька значень результативної ознаки. В кореляційних зв’язках між причиною і наслідком немає повної відповідності, а спостерігається лише певне співвідношення.

Для багатофакторних моделей чи явищ доцільно використовувати методи множинного кореляційно-регресійного аналізу, які дають змогу вивчити та кількісно оцінити внутрішні і зовнішні наслідкові зв’язки між утворюючими модель факторами та встановити закономірності функціонування і тенденції розвитку досліджуваної результативної ознаки.

Кореляційний метод аналізу розв’язує два основних завдання:

1) визначає за допомогою рівняння регресії аналітичну форму зв’язку між варіацією ознак «х» і «у»;

2) встановлює міру тісноти зв’язку між ознаками.

У реальному житті трапляється так, що один визначальний фактор залежить від кількох різних чинників, між якими не можна встановити явного зв’язку. У цьому випадку доцільно наоснові методів багатофакторного кореляційно регресійного аналізу створити математичну модель процесу чи явища, яка дала би змогу оцінити ступінь впливу на досліджуваний результативний показник кожного із введених у модель факторів при фіксованому положенні на середньому рівні інших факторів.

Для побудови багатофакторних регресійних моделей виділимо такі етапи:

1. Підбір усіх факторів, що впливають на досліджуваний показник та визначення до кожного числової характеристики.

2. Вибір вигляду моделі, тобто знаходження аналітичного виразу, котрий найкраще відображував би зв'язок факторних ознак з результативною, тобто вибір функції: Yˆ = f (X1,X2,X3,... ,Хn), де Yˆ – результативна ознака-функція; Х1,Х2,Х3,…,Хn – факторні ознаки.

3. Перевірка адекватності отриманої моделі. Для цього необхідно обчислити:

– залишки моделі, тобто розбіжності між спостереженими та розрахунковими значеннями:

uі = yі – ŷі = yі – (а0 + а1Х1і+ а2Х2і + … + аnXni), і = 1,2,…,m;

– відносну похибку залишків та її середнє значення:

, ;

– середньоквадратичну помилку дисперсії збурень:

;

– коефіцієнт детермінації:

;

– коефіцієнт множинної кореляції r , який є основним показником щільності кореляційного зв’язку узагальненого показника з факторами:

[1].

Всі значення коефіцієнта кореляції r належать інтервалу від -1 до 1. Знак

коефіцієнта показує “напрямок” зв'язку: додатне значення свідчить про “прямий” зв'язок, від'ємне значення – про “зворотний” зв'язок, а значення “0”– про відсутність лінійного кореляційного зв'язку. При r = 1 або r = –1 маємо функціональний зв'язок між ознаками.

4. Перевірка адекватності моделі. Перевірка здійснюється за допомогою статистики Фішера з n та (m-n-1) ступенями вільності:

де n – кількість факторів,що увійшли в модель; m – загальна кількість спостережень; r – коефіцієнт множинної кореляції.

За таблицями Фішера знаходиться критичне значення Fкр з n та (m-n-1) ступенями вільності. Якщо F>Fкр, то це свідчить про адекватність побудованої моделі. Якщо модель не адекватна, то необхідно повернутися до етапу побудови моделі і, можливо, ввести додаткові фактори або перейти до нелінійної моделі.

5. Перевірка значущості коефіцієнтів рівняння регресії. Перевірка здійснюється за допомогою t-статистики, яка для параметрів багатофакторної регресії має вигляд:

де ai s – середньоквадратичне відхилення оцінки і-го параметра.

Якщо значення ti перевищує критичне значення, яке знаходиться за таблицями t-критерію Стьюдента, то відповідний параметр є статистично значимим і має істотний вплив на узагальнюючий показник.

6. Обчислення коефіцієнта еластичності. Відмінності в одиницях вимірювання факторів усувають використанням часткових коефіцієнтів еластичності, що задаються співвідношенням:

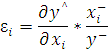
де xi – середнє значення і-го параметра; y – середнє значення результативної

ознаки.

Частковий коефіцієнт еластичності εi вказує, на скільки відсотків в середньому змінюється результативна ознака із зміною на 1% фактора хі при фіксованому значенні інших параметрів.

7. Визначення довірчих інтервалів для параметрів регресії. Довірчий інтервал при рівні надійності (1-ɑ) є інтервал з випадково визначеними межами, що з рівнем довіри (1-ɑ) накриває істинне значення коефіцієнта рівняння регресії аi і задається залежностями:

(ai-tɑ/2,kσ2 ai; ai+tɑ/2,kσ2ai)

де tɑ/2,k – статистика Стьюдента з к = m – n – 1 ступенями свободи і рівні значущості ɑ; σ2ai –середньоквадратичне відхилення оцінки параметра аi [1].

Отже, за допомогою наведеної розрахункової процедури багатофакторного кореляційно-регресійного аналізу ми можемо оцінити вплив кожного із чинників, що утворюють модель процесу чи явища, на результативну ознаку і спрогнозувати поведінку об’єкта на майбутнє.

Дані моделі кореляційного аналізу доцільно застосовувати при розв’язанні задач на опрацювання експериментальних даних. Такі моделі статистичних методів дозволяють здійснювати адекватний вибір статистичного методу опрацювання експериментальних даних шляхом порівняння й аналізу ознакової моделі даних в умові задачі і множини ознакових моделей статистичних методів, які відповідають постановці умови задачі.

Список використаних джерел:

1. Степанишин В.М., Тисовський Л.О. Побудова моделі кореляційного аналізу для дослідження багатофакторних процесів і явищ/ В.М. Степанишин, Л.О. Тисовський.- НЛУУ.-2012. С. 133-138.

2. Хоменко С. В., Павленко Л. В. Побудова узагальнених ознакових моделей опису статистичних методів кореляційного аналізу у експериментальних даних для навчання майбутніх інженерів-педагогів/ С. В.Хоменко, Л. В. Павленко. – БДПУ.- 2011.