Физика/1. Теоретическая физика

В.Г. Власенко, И.В. Волчок,
Л.М. Калиберда, А.И. Спольник, М.А. Чегорян

Харьковский национальный технический университет

сельского хозяйства имени П. Василенко

Рассеяние дейтонов средних энергий

В настоящей работе показано, что с использованием метода перевала, можно рассмотреть упругое рассеяние частиц с I = 1 на бесспиновых ядрах. Получены выражения, описывающие сечения и поляризацию дейтонов. Если энергия налетающих частиц Е значительно больше кулоновского барьера , то амплитуду процесса можно записать, пренебрегая членами, описывающими кулоновское рассеяние в виде:

(1)

где и - проекции спинов соответственно налетающей и рассеянной частиц;

и - орбитальные моменты во входном и выходном каналах.

Ось квантования выбрана вдоль z, а ось у перпендикулярна плоскости рассеяния. В (1), учитывая сохранение пространственной четности, можно выполнить суммирование по ,;,; . При этом (1) разбивается на пять выражений, два из них описывают рассеяние без переворота спина ), а три других ) – с переворотом спина.

Рассмотрим случай малого спин-орбитального взаимодействия, когда

, а ),

при этом . Разлагая матрицу рассеяния в ряд по степеням с точностью до квадратичных членов и переходя от суммирования к интегрированию в области комплексных , получим, используя метод перевала:

,

,

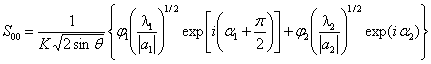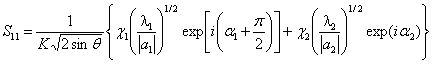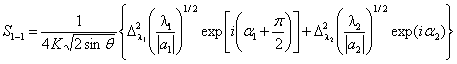, (2)

,

,

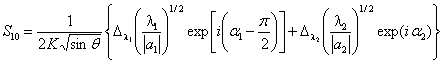где – седловые точки, ближайшие к действительной оси;

, ,

, , .

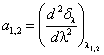Мы воспользовались асимптотическим выражением для сферических функций при :

.

Сечение упругого рассеяния и спин-тензоры поляризации рассеянных частиц могут быть записаны при использовании (2) в следующем виде:

, (3)

, (4)

, (5)

, (6)

, (7)

. (8)

Остальные спин-тензоры связаны с приведенными соотношениями

.

В формулах (3) – (8) введены следующие обозначения:

, , ,

,

, , .

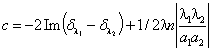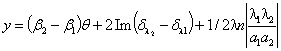Полученные формулы позволяют описывать сечение упругого рассеяния и поляризацию дейтонов на бесспиновых ядрах.